Формули перерахунку для основних типів комбінаторних з’єднань

З’єднання	Без повторень елементів	З повтореннями елементів
Перестановки
Розміщення
Сполучення

Тема№3 Принцип включення-виключення

Нехай є деяка скінченна множина , що має потужність у об'єктів та множина властивостей Кожний об'єкт множини може володіти або не володіти однією або одночасно декількома (всіма) властивостями із множини .

Введемо ряд позначень.

– кількість об'єктів множини , які володіють властивістю ;

–кількість об'єктів, щоне володіють властивістю ;

–кількість об'єктів, що володіють двома властивостями одночасно;

– кількість об'єктів, що володіють трьома властивостями одночасно;

– кількість об'єктів, що володіють усіма властивостями множини одночасно;

– кількість об'єктів, що не володіють ні одним з властивостей множини .

Теорема 4

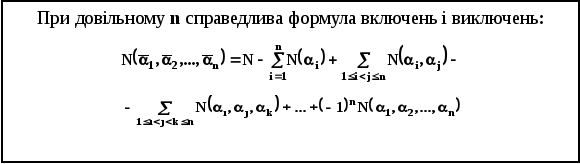
Доведення.

Формула включень та виключень визначає кількість об'єктів, що не володіють ні однією з властивостей, заданих множиною .

Наприклад:

На фірмі працює67 співробітників.З них 47 володіють англійською мовою, 35 – німецькою, 20 – французькою; одночасно англійською та німецькою володіють – 23 співробітника, англійською та французькою – 12, німецькою та французькою – 11, трьома мовами володіють 5 співробітників. Скільки співробітниківне володіють ні однієюіз перерахованих мов?

Розв’язання.

Визначимо наступні властивості:

– "володітианглійською мовою”;

– "володіти німецькою мовою;

– "володіти французькою мовою".

За формулою включень і виключень маємо:

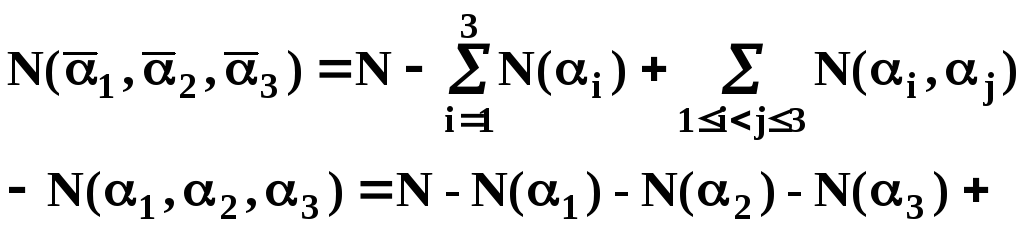
Окремі випадки формули включень і виключень

1. Якщо всі властивості попарно несумісні, тобто

то формула включень і виключень має вигляд:

2. Якщо кожне число залежить не від характеру властивостей, а лишевід їх кількості, то формула має вигляд:

де – кількість об’єктів, що володіють рівно властивостями.

Задача про безлад

Нехай є множина

Розглянемо перестановки елементів множини .

Елементперестановки називається нерухомим, якщо, тобто елемент стоїтьна своєму місці.

Наприклад.

При у перестановці – елемент– нерухомий, а у перестановці –усі елементи нерухомі.

Безладом називаєтьсяперестановка, яка не має нерухомих елементів, тобто

Постановка задачі

Визначити – кількістьбезладів у-елементній множині, або кількістьперестановок чиселтаких, що.

Розв’язання.

Загальнечисло перестановоку -елементній множині дорівнює. Позначимочерез таку властивістьперестановки,що-й елемент стоїтьна своєму місці, тобто. Тоді ліва частина формули включень та виключень і є розв’язком задачі про безлад. За позначеннямє кількість перестановок в-елементній множині, у яких один-тий елемент стоїть на своєму місці і дорівнює, бо один елемент не можна переставляти, а останні елементи можуть бути переставленіспособами. Так як число перестановок не залежить відтого, який саме елемент знаходитьсяна своєму місці, то:

:

Аналогічно, визначимо – кількість перестановок, у яких рівно два елементи знаходяться на своїх місцях: та, відповідно, – кількістьперестановок,у яких тільки елементів знаходятьсяна своїх місцях: .

За формулою включень-виключень маємо:

Розпишемоформулу

–ще називають субфакторіалом.