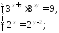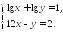- •Содержание
- •Требования к результатам обучения
- •Алгебра (Развитие понятия о числе. Корни, cтепени, логарифмы. Основы тригонометрии)
- •Функции (Функции, их свойства и графики)
- •Начала математического анализа
- •Уравнения и неравенства
- •Стохастика (Элементы комбинаторики. Элементы теории вероятностей и математической статистики)
- •Геометрия (Прямые, плоскости и углы в пространстве. Координаты и векторы. Многогранники, тела и поверхности вращения. Элементы вычислительной геометрии)
- •Объем дисциплины и виды учебной работы
- •Тематический план
- •Программа курса
- •Тема 1. «Развитие понятия о числе»
- •Тема 2. «Корни, степени, логарифмы»
- •Тема 3. «Элементы комбинаторики»
- •Тема 4. «Прямые, плоскости и углы в пространстве»
- •Тема 5. «Основы тригонометрии»
- •Тема 6. «Координаты и векторы»
- •Тема 7. «Функции, их свойства и графики»
- •Тема 8. «Многогранники, тела и поверхности вращения»
- •Тема 9. «Начала математического анализа»
- •Тема 10. «Элементы вычислительной геометрии»
- •Тема 11. «Элементы теории вероятностей и математической статистики»
- •Тема 12. «Уравнения и неравенства»
- •Методические рекомендации по изучению дисциплины и организации самостоятельной работы студентов
- •Задания для самостоятельной работы студентов.
- •Тригонометрические преобразования.
- •Вероятность
- •Геометрия
- •Параллельность прямых в пространстве.
- •Параллельность прямой и плоскости
- •Параллельность двух плоскостей
- •Угол между прямыми в пространстве. Перпендикулярность прямых
- •Угол между прямой и плоскостью. Перпендикулярность прямой и плоскости
- •Угол между плоскостями. Перпендикулярность плоскостей
- •Примерные темы докладов и рефератов
- •Рекомендуемая литература1
- •Основная
- •Дополнительная
- •Справочные материалы
- •Контрольные задания по темам
- •(Подготовительные варианты)
- •Тема 1.«Развитие понятие о числе»
- •Тема 2.«Корни, степени, логарифмы»
- •Тема 3.«Элементы комбинаторики»
- •Тема 4.«Прямые, плоскости и углы в пространстве»
- •Тема 5.«Основы тригонометрии»
- •Тема 6.«Координаты и векторы»
- •Тема 7.«Функции, их свойства и графики»
- •Тема 8.«Многогранники и тела вращения»
- •Тема 9.«Начала математического анализа»
- •Тема 10.«Элементы вычислительной геометрии»
- •Тема 11. «Элементы теории вероятностей и математической статистики»
- •Тема 12.«Уравнения и неравенства»
- •Итоговые контрольные задания
- •(Подготовительные варианты)
- •Итоговые контрольные задания № 1
- •Итоговые контрольные задания № 2
- •Приложение
- •Типовые задания, соответствующие требованиям, предъявляемым к результатам обучения.
- •Алгебра. Функции, уравнения и неравенства.
- •Начала математического анализа
- •Геометрия
- •Cтохастика (комбинаторика, теория вероятностей и математическая статистика)
Итоговые контрольные задания № 2
К каждому заданию дано несколько ответов. Укажите верный ответ, сопроводив задание кратким решением.
Упростите выражение:
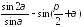 .
. ;
; ;
; ;
; .
.
Решите уравнение:
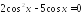 .
.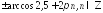 ;
;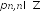 ;
;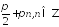 ;
;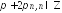 .
.
Найдите производную функции
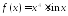 .
.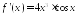 ;
;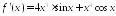 ;
;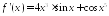 ;
;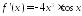 .
.
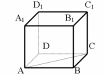
Ребро куба
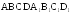 равно 4. Найдите расстояние от вершины
равно 4. Найдите расстояние от вершины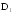 до прямой
до прямой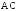 .
.
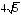 ;
;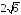 ;
;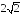 ;
;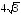 .
.
Решите неравенство
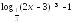 .
.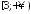 ;
;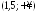 ;
;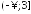 ;
;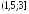 .
.
Найдите промежутки убывания функции
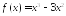 .
. ;
; ;
; ;
;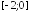 .
.
Найдите диагональ правильной четырехугольной призмы, если сторона основания
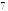 ,
высота
,
высота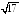 .
.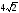 ;
;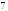 ;
;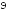 ;
;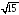 .
.
Найдите объем конуса, полученного в результате вращения прямоугольного треугольника с гипотенузой
 и
острым углом
и
острым углом вокруг меньшего катета.
вокруг меньшего катета.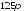 ;
; ;
; ;
;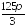 .
.
Из данных выражений выберите то, которое имеет смысл.
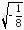 ;
; ;
;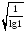 ;
;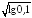 .
.
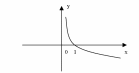
Укажите, график какой функции схематично изображен на рисунке.
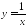 ;
;
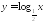 ;
;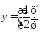 ;
;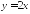 .
.
Найдите функцию, для которой функция
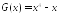 является первообразной.
является первообразной.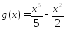 ;
;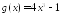 ;
;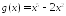 ;
;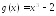 .
.
Решите уравнение
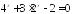 .
.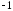 ;
;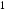 ;
; ;
;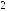 .
.
Приложение
Типовые задания, соответствующие требованиям, предъявляемым к результатам обучения.
Ниже приводится набор типовых заданий, для выполнения которых обучающимися должны быть успешно применены сформированные умения.
Алгебра. Функции, уравнения и неравенства.
Вычислите значение выражения:
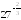 ;
;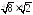 ;
; ;
;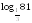 ;
; ;
;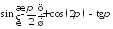 ;
;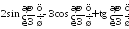
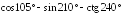 ;
;
Сравните числа:
 и
и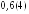 ;
;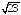 и
и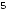 ;
;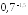 и
и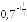 ;
;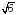 и
и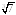 ;
;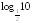 и
и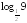 ;
;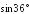 и
и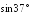 .
.
Найдите числовое значение выражения:
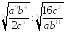 ,
если
,
если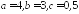 ;
;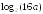 ,
если
,
если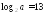 ;
;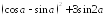 ,
если
,
если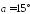 .
.
Вычислите:
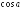 и
и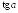 ,
если
,
если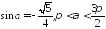 ;
;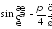 ,
если
,
если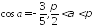 ;
;
Упростите выражение:
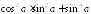 ;
;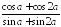 ;
;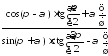 .
.
Установите, при каких значениях
 имеет смысл выражение:
имеет смысл выражение:
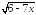 ;
;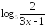 ;
;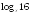 ;
;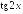 .
.
Выясните, какое из двух уравнений является следствием другого:
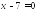 и
и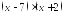 ;
;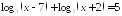 и
и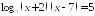 .
.
Выясните, равносильны ли уравнения:
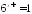 и
и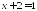 ;
;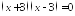 и
и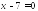 .
.
Решите уравнения:
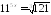 ;
;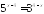 ;
;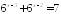 ;
;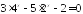 .
.
Решите уравнения:
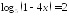 ;
;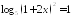 ;
;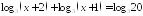 ;
;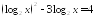 .
.
Решите уравнения:
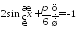 ;
;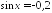 ;
;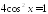 ;
;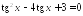 .
.
Решите уравнения:
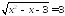 ;
;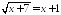 .
.
Решите неравенства:
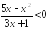 ;
;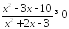 ;
; ;
;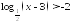 .
.
Решите систему уравнений:
Найдите область определения функции:
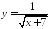 ;
;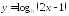 .
.
Функция задана формулой
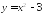 .
Найдите:
.
Найдите: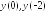 ;
;значение
 ,
при котором
,
при котором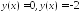 .
.
Выясните, принадлежит ли графику функции
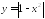 точка
точка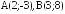 .
.Постройте график функции. Найдите точку (точки) его пересечения с какой-либо осью (с осями) координат и значения
 ,
при которых функция принимает
положительные значения:
,
при которых функция принимает
положительные значения:
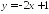 ;
;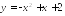 ;
;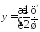 ;
;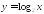 .
.
Решите графически уравнение:
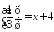 ;
;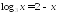 .
.
Установите, возрастающей или убывающей является функция:
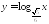 ;
;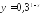 .
.
Найдите множество значений функции:
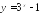 ;
;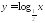 ,
если
,
если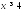 ;
;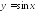 ,
если
,
если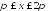 .
.
Выясните, является ли чётной или нечётной функция:
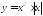 ;
;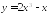 ;
;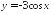 .
.
Начала математического анализа
Постройте касательную к параболе:
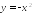 в точке
в точке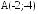 ;
;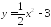 в точке
в точке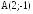 .
.
Найдите производную функции:
 ;
;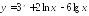 ;
;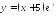 ;
;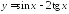 ;
;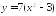 ;
; .
.
Найдите производную функции:
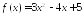 в точке
в точке ;
;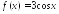 в точке
в точке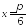 .
.
Запишите уравнение касательной к графику функции:
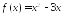 в точке
в точке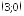 ;
;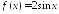 в точке с абсциссой
в точке с абсциссой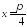 .
.
Найдите промежутки монотонности функции:
 ;
;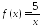 ;
;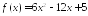 ;
;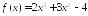 .
.
Найдите точки экстремума и экстремумы функции:
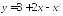 ;
;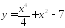 .
.
Вычислите интеграл:
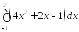 ;
;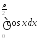 .
.
Найдите площадь фигуры, ограниченной линиями:
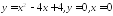 ;
;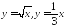 .
.Геометрия
Изобразите куб
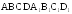 и укажите:
и укажите:прямые, параллельные прямой
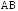 ;
;прямые, пересекающиеся с прямой
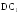 ;
;прямые, скрещивающиеся с прямой
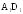 ;
;плоскость, параллельную плоскости
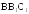 .
.
Две прямые параллельны некоторой плоскости. Могут ли эти прямые:
пересекаться;
быть параллельными;
быть скрещивающимися?
Через точку
 пересечения диагоналей прямоугольника
пересечения диагоналей прямоугольника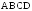 проведена прямая
проведена прямая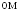 ,
перпендикулярная плоскости прямоугольника.
Найдите длину отрезка
,
перпендикулярная плоскости прямоугольника.
Найдите длину отрезка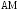 ,
если
,
если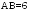 ,
,
 ,
,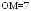 .
.
Из некоторой точки проведены к данной плоскости перпендикуляр и наклонная, угол между которыми
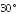 .
Найдите наклонную и её проекцию на
плоскость, если длина перпендикуляра
5 см.
.
Найдите наклонную и её проекцию на
плоскость, если длина перпендикуляра
5 см.
Найдите диагональ прямоугольного параллелепипеда, если его измерения равны 7, 9 и
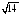 .
.
В правильной четырёхугольной пирамиде сторона основания равна 4 см, а угол наклона боковой грани к плоскости основания равен
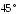 .
Найдите площадь боковой поверхности
пирамиды.
.
Найдите площадь боковой поверхности
пирамиды.
Основанием прямой призмы является равносторонний треугольник со стороной 6 см. Высота призмы равна 4 см. Найдите площадь поверхности призмы.
Апофема правильной шестиугольной пирамиды равна
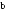 ,
а радиус описанной около основания
окружности равен
,
а радиус описанной около основания
окружности равен .
Найдите площадь боковой поверхности
этой пирамиды.
.
Найдите площадь боковой поверхности
этой пирамиды.
Что представляет собой сечение цилиндра плоскостью, проходящей:
через две образующие;
через некоторую точку поверхности перпендикулярно оси?
Что представляет собой сечение конуса плоскостью, проходящей:
через ось конуса;
через точку поверхности перпендикулярно оси;
через две образующие?
Сколько квадратных метров листовой жести пойдёт на изготовление трубы длиной 3 м и диаметром 40 см, если на швы необходимо добавить 2% площади её боковой поверхности?
Найдите высоту конуса, если площадь его осевого сечения равна 10 см2,а площадь основания равна 6 см2.
Игрушечное ведёрко имеет форму усечённого конуса, радиусы оснований которого равны 7 см и 13 см, а образующая равна 10 см. Найдите:
высоту ведёрка;
массу краски, необходимой для окраски этого ведёрка с обеих сторон, если на окраску 1 см2требуется 0,2 г краски.
Площадь сечения сферы, проходящего через её центр равна 7 дм2. Найдите площадь поверхности сферы.
Диагональ прямоугольного параллелепипеда равна 12 см и составляет угол
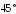 с плоскостью основания и
с плоскостью основания и с ребром основания. Найдите объём
параллелепипеда.
с ребром основания. Найдите объём
параллелепипеда.
Найдите объём правильной треугольной пирамиды:
высота которой 10 см, а сторона основания 6 см;
апофема которой равна 8 см и составляет
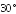 с плоскостью основания.
с плоскостью основания.
Какова вместимость цистерны, имеющей форму цилиндра с диаметром 4 м и длиной 10 м?
Найдите объём конуса, имеющего высоту h, равную диаметру основания.
Стороны оснований правильной усечённой четырёхугольной пирамиды равны 10 см и 18 см, апофема равна 5 см. Найдите объём усечённой пирамиды.
Найдите массу метеорита, имеющего форму шара радиуса 1 м, если плотность составляющего её вещества равна 3 г/см3.