Pobegailo

учитывая равенство (3.1). В результате получили, что множество O(3, R) удовлетворяет всем условиям группы. Следовательно, множество O(3, R)

вместе с операцией умножения матриц образует группу. Эта группа называется ортогональной группой третьего порядка над полем действительных чисел R и обозначается O(3, R). Элементы группы O(3, R) назы-

ваются ортогональными матрицами. Ортогональные матрицы имеют следующие свойства.

Свойство 1. Произвольная ортогональная матрица R удовлетворяет тождеству

RRT = I.

Доказательство. Пусть R – произвольная ортогональная матрица. Тогда, используя равенство (3.1), получим

RRT = (RT R)T = IT = I.

Свойство доказано.

Свойство 2. Произвольная ортогональная матрица R удовлетворяет тождеству

R−1 = RT .

Доказательство. Пусть R – произвольная ортогональная матрица. Тогда, используя равенство (3.1) и свойство 1, получим

RT R = RRT = I.

Из этого равенства следует, что

R−1 = RT .

Свойство доказано.

Свойство 3. Для произвольной ортогональной матрицы R справедливы равенства

det R = ±1.

Доказательство. Пусть R – произвольная ортогональная матрица. Тогда, используя равенство (3.1), получим

(det R)2 = det Rdet R = det(RT )det R = det(RT R) = det I =1.

Отсюда следует, что

det R = ±1.

Свойство доказано.

Покажем, что действие ортогональных матриц на векторы сохраняет длины векторов. Для этого рассмотрим произвольный вектор v R3, про-

60

извольную ортогональную матрицу R и вычислим длину вектора, преобразованного посредством матрицы R. Получим

| Rv | = (Rv) (Rv) = (Rv)T Rv = vT RT Rv = vT v = v v =| v |.

Отсюда следует, что преобразования, описываемые ортогональными матрицами, сохраняют расстояния между точками в евклидовом аффин-

ном пространстве E3.

Обозначим через SO(3, R) подмножество ортогональных матриц из множества O(3, R), которые имеют следующее свойство:

Покажем, что множество SO(3, R) образует подгруппу группы O(3, R) . Для этого рассмотрим произвольные матрицы R и Q из множества SO(3, R). Произведение этих матриц RQ также принадлежит множеству SO(3, R), так как

det(RQ) = det Rdet Q =1.

Очевидно, что множество SO(3, R) содержит единичную матрицу I, которая является нейтральным элементом относительно операции умножения матриц. Кроме того, для любой матрицы R из множества SO(3, R)

существует обратная матрица R−1, которая также принадлежит множеству SO(3, R), так как

det R−1 = det1 R =1.

В результате получили, что множество SO(3, R) вместе с операцией умножения матриц образует подгруппу группы O(3, R). Эта подгруппа на-

зывается специальной ортогональной группой третьего порядка над по-

лем действительных чисел R и обозначается через SO(3, R). Элементы группы SO(3, R) называются собственно ортогональными матрицами.

Пример. Рассмотрим матрицу

Очевидно, что

61

и, кроме того,

det R =1.

Следовательно, матрица R является собственно ортогональной.

3.2. Автоморфизмы сферы

Рассмотрим сферу S 2 в евклидовом аффинном пространстве E3, которая описана каноническим уравнением

x2 + y2 + z2 = r2

относительно некоторой ортонормированной системы координат. Используя матричную нотацию, это уравнение может быть записано следующим образом:

где p обозначает радиус-вектор произвольной точки P E3, а S – матрицу квадратичной формы

S(x, y, z) = x2 + y2 + z2 ,

которая, очевидно, имеет следующую структуру:

Геометрическое преобразование сферы саму в себя, называется ав-

томорфизмом сферы.

Ортогональным поворотом называется линейное преобразование

ρ: E3 → E3,

которое удовлетворяет условию

ρ(S 2 ) = S 2.

Это значит, что точки, лежащие на сфере S2 , под действием ортогонального поворота ρ преобразуются также в точки, лежащие на сфере S 2. Из

62

определения ортогонального поворота следует, что ортогональные повороты это линейные автоморфизмы сферы S 2.

Обозначим через R матрицу ортогонального поворота ρ относительно рассматриваемой системы координат. Тогда из определения ортогонального поворота следует, что

pT Sp = (Rp)T S(Rp)

для любой точки P S 2. Преобразуем это равенство следующим образом:

pT Sp = pT (RT SR) p.

Так как радиус-вектор p был выбран произвольно, то из полученного равенства следует, что

S = RT SR.

Принимая во внимание структуру матрицы S, из последнего равенства следует, что

I = RT R.

Если к тому же матрица поворота удовлетворяет условию det R =1,

то ортогональный поворот будет называться собственным ортогональ-

ным поворотом.

В результате получили, что ортогональные повороты представляются ортогональными матрицами группы O3, а собственно ортогональные повороты – собственно ортогональными матрицами группы SO(3, R). Отсюда следует, что ортогональные повороты сохраняют длину векторов в евклидовом векторном пространстве R3 и, следовательно, расстояние

между точками в евклидовом аффинном пространстве E3. Заметим, что из сохранения длины векторов следует сохранение ортогональными поворотами также и углов между векторами.

Так как в дальнейшем будут рассматриваться только собственно ортогональные повороты, то такие повороты будут также часто называться просто поворотами.

3.3. Геометрическое построение поворота

Из определения поворота следует, что это такое геометрическое преобразование, которое поворачивает евклидово аффинное пространство

E3 вокруг линии, проходящей через начало системы координат.

63

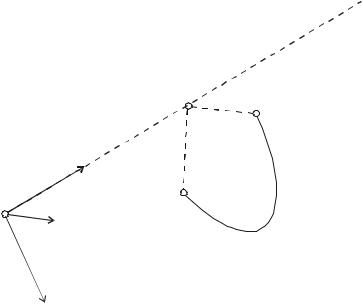
Найдем векторное выражение для представления поворота. Для этого рассмотрим произвольную прямую L, проходящую через начало системы

координат O, и возьмем произвольную точку P из пространства E3. Пусть Q обозначает точку, которая получена из точки P путем ее поворота на угол φ вокруг прямой L. Для нахождения векторного представления этого поворота выберем некоторую ортонормированную систему координат (O, x, y, z), начало которой O лежит на прямой L. Обозначим через

n единичный осевой вектор, направленный вдоль прямой L. Пусть p и q обозначают радиус-векторы точек P и Q соответственно.

Для того чтобы найти соотношение между координатами точек P и Q, определим новую ортонормированную систему координат (O, l,m, n),

оси которой направлены следующим образом. Ось l направлена вдоль ортогональной проекции вектора p на плоскость, перпендикулярную единичному вектору n и проходящую через начало координат O, а ось m определена следующим образом:

Построение системы координат (O, l,m, n) проиллюстрировано на рис. 3.1.

L

P

n

m

Рис. 3.1. Геометрическое построение поворота

Теперь представим радиус-вектор p как сумму его проекций на оси n и l следующим образом:

64

Определим вектор

Видно, что вектор r – это единичный вектор, который получен поворотом вектора l вокруг оси n на угол ϕ. Тогда радиус-вектор q можно представить как сумму его проекций на оси n и r следующим образом:

Так как повороты сохраняют длину векторов и углы между векторами, то из сравнения равенств (3.5) и (3.7) следует, что

q n = p n, q r = p l.

Подстановка этих значений в равенство (3.7) дает следующее равенство:

Теперь преобразуем равенство (3.8), используя равенства (3.4), (3.6) и (3.9). Получим

q= ( p n)n +( p l)(cosϕl +sin ϕm) =

=( p n)n +cosϕ( p l)l +sin ϕ( p l)m =

=( p n)n +cosϕ( p l)l +sin ϕ( p l)(n ×l) =

=( p n)n +cosϕ( p l)l +sin ϕ(n ×( p l)l) =

=( p n)n +cosϕ( p −( p n)n) +sin ϕ(n ×( p −( p n)n)) =

=( p n)n +cosϕ( p −( p n)n) +sin ϕ(n × p).

Таким образом, в результате получили, что поворот на угол φ вокруг прямой L, используя операции векторной алгебры, описывается следующим образом:

3.4. Представление поворотов матрицами группы SO(3, R)

Определим структуру собственно ортогональной матрицы, которая описывает поворот. Для этого рассмотрим векторное преобразование, заданное формулой (3.10). Чтобы представить это преобразование в матричном виде, определим следующие матрицы:

65

Теперь, принимая во внимание, что

( p n)n = Mp, n × p = Kp,

равенство (3.10) может быть переписано, используя введенные матрицы M и N, следующим образом:

q= Mp +cos ϕ( p − Mp) +sin ϕKp = Mp +cosϕ(I − M ) p +sin ϕKp =

=(M +cosϕ(I − M ) +sin ϕK ) p.

Определим матрицу

R(n,ϕ) = M +cosϕ(I − M ) +sin ϕK.

Из этого равенства следует, что матрица R(n,ϕ) имеет следующую структуру:

где используется следующее обозначение: versϕ =1−cosϕ.

Определенная выше матрица R(n,ϕ) является координатным представ-

лением поворота вокруг оси n на угол φ относительно ортонормированной системы координат (O, x, y, z).

Из формулы (3.11) следует, что повороты вокруг координатных осей x, y и z на углы α, β и γ соответственно описываются следующими матрицами:

66

Покажем, что матрица поворота R(n,ϕ) является собственно ортогональной. Видно, что матрицы M и N удовлетворяют следующим условиям:

MT M = M,

MT K = KT M = 0,

KT K = I − M.

Из этих равенств следует, что

RT (n,ϕ)R(n,ϕ) =

=(M +cosϕ(I − M ) +sin ϕK )T (M +cosϕ(I − M ) +sin ϕK ) =

=MT M +cosϕ(M − MT M ) +sin ϕMT K +

+cosϕ(M − MT M ) +cos2 ϕ(I − 2M + MT M ) +sin ϕcosϕ(K − MT K ) +

+sin ϕKT M +sin ϕcosϕ(K − KT M ) +sin2 ϕKT K =

=M +cos2 ϕ(I − M ) +sin2 ϕ(I − M ) = I.

Врезультате доказали, что матрица R(n,ϕ) является ортогональной. Кроме того,

det R(n,ϕ) =1,

так как систему координат в евклидовом аффинном пространстве всегда можно выбрать так, что прямая, вокруг которой выполняется поворот, будет совпадать с осью z этой системы координат. Легко вычислить, что в этом случае

R(z, γ) =1.

Но определитель матрицы геометрического преобразования не зависит от выбора системы координат, относительно которой описано это геометрическое преобразование. Следовательно, определитель любой матрицы поворота также равен 1. Получили, что матрицы поворота являются собственно ортогональными, т. е. принадлежат матричной группе

SO(3, R).

Решим обратную задачу, т. е. найдем ось n и угол ϕ поворота, который представлен некоторой ортогональной матрицей

67

Для решения этой задачи рассмотрим формулу (3.11), которая описывает структуру собственно ортогональной матрицы R(n,ϕ). Сравнивая

элементы матриц R и R(n,ϕ), получим следующее выражение для определения угла ϕ:

Тогда координаты оси n могут быть определены следующим образом:

при условии, что

ϕ ≠ 0, ϕ ≠ π.

Иначе координаты оси n определяются следующим образом:

Пример. Рассмотрим матрицу

которая, как было показано в примере из раздела 3.1, является собственно ортогональной. Найдем ось и угол поворота, который представляет эта матрица. Сначала, используя формулы (3.12)–(3.14), найдем угол поворота, получим

68

Отсюда следует, что

ϕ = π4 .

Теперь, используя формулы (3.16), найдем координаты оси поворота, получим

n1 = 0, n2 = 0, n3 =1.

Этот же результат можно было бы получить, если заметить, что структура матрицы R совпадает со структурой матрицы R(z, γ), которая

описывает поворот вокруг оси координат z.

3.5. Собственные векторы и значения поворотов

Рассмотрим некоторый поворот, который представлен собственно ортогональной матрицей R(n,ϕ) относительно некоторой ортонормирован-

ной системы координат. Предположим, что угол этого поворота удовлетворяет условию

при k N. Для того чтобы упростить дальнейшие вычисления, определим такую новую ортонормированную систему координат (O, x, y, z), ось z

которой совпадает с осью n поворота R(n,ϕ). В разделе 3.4 было показа-

но, что в этом случае матрица рассматриваемого поворота относительно новой системы координат (O, x, y, z) имеет следующую структуру:

Так как собственные векторы и собственные значения геометрического преобразования инвариантны относительно выбора системы координат, относительно которой описано это геометрическое преобразование, то собственные векторы и собственные значения матрицы R(z,ϕ) совпа-

дают с собственными векторами и собственными значениями матрицы R(n,ϕ). Однако следует учитывать, что координаты этих векторов опре-

делены относительно разных систем координат. Собственные значения матрицы R(z,ϕ) могут быть найдены из следующего характеристическо-

го уравнения:

det(R(z,ϕ) −λI) = 0,

69