Pobegailo

Из этого следует, учитывая равенства (7.1) и (7.2), что c0 = 0.

Следовательно, равенство (7.14) может быть переписано следующим образом:

c1bn,1(u) +c2bn,2 (u) +c3bn,3 (u) + +cnbn,n (u) = 0.

Разделив это равенство на bn,1(u), получим

Это равенство можно переписать следующим образом:

Отсюда следует, что

c1 = 0.

Повторяя аналогичные рассуждения дальше, получим, что все коэффициенты ci при i {0, 1, ..., n} равны нулю. Следовательно, полиномы Берн-

штейна bn,m (u) , где m {0, 1, ..., n}, являются линейно независимыми.

Теорема доказана.

Теорема 2. Любой полином степени n может быть представлен единственной линейной комбинацией полиномов Бернштейна bn,m (u) , где

m {0, 1, ..., n}.

Доказательство. Рассмотрим произвольный полином

степени n, где u [0, 1]. Покажем, что полином p(u) может быть представлен единственной линейной комбинацией

c0bn,0 (u) +c1bn,1(u) + +cnbn,n (u) = p(u) ,

где ci R для i {0, 1, ..., n}. Это равенство эквивалентно следующей системе уравнений:

150

c0bn,0 (u) +c1bn,1(u) + +cnbn,n (u) = p(u),

уравнения значения u = 0 дает следующую систему уравнений:

Принимая во внимание, что полиномы Бернштейна и их производные удовлетворяют граничным условиям, описанным соответственно равенствами (7.1) и (7.2) и равенствами (7.3), (7.5) и (7.7), полученная система уравнений эквивалентна следующей системе уравнений:

Разрешая эту систему относительно неизвестных коэффициентов ci , где i {0, 1, ..., n}, получим

151

Следовательно, полином p(u) может быть представлен единственной линейнойкомбинациейполиномовБернштейна bn,m (u), где m {0, 1, ..., n}.

Теорема доказана.

Из теорем 1 и 2 следует, что полиномы Бернштейна bk,m (u), где k {0, 1, ..., n}, образуют базис для всех полиномов степени не больше

чем n.

Пример. Представим полином

p(u) =1+2u +3u2 ,

где u [0, 1], линейной комбинацией полиномов Бернштейна. В этом случае нужно найти такие действительные числа c0 , c1 и c2 , что

c0b2,0 (u) +c1b2,1(u) +c2b2,2 (u) =1+ 2u +3u2.

Найдем коэффициенты c0 , c1 и c2 , используя формулу (7.14). Для этой цели найдем первые две производные полиномов Бернштейна

Получим

Кроме того, найдем первые две производные от полинома p(u). Получим p′(u) = 2 +6u, p′′(u) = 6.

Тогда, используя формулы (7.15), искомые коэффициенты определяются следующим образом:

В результате получили

1+2u +3u2 = (1−u)2 +2(2(1−u)u) +6u2.

152

7.5. Сглаживающие полиномы

В этом разделе определим полиномы, которые аппроксимируют ступенчатую функцию

Эти полиномы могут использоваться для сглаживания разрывов функций. Но они также имеют и геометрические приложения. В дальнейшем будет показано, как с помощью этих полиномов можно выполнять гладкий переход между однопараметрическими группами Ли.

Очевидно, что ступенчатая функция δ(u) является бесконечно глад-

кой на границах интервала [0,1] и имеет разрыв в середине этого интервала. Чтобы избежать этого разрыва, аппроксимируем ступенчатую функцию δ(u) полиномами. Для этого введем следующие последовательности

узловых точек:

(0, 1), (0, 0, 1, 1),

(0, 0, ..., 0,1,1, ...,1)

k +1 k+1

для любых k {0,1, ...}. Тогда, используя полиномы Бернштейна

bn,m (u) = Cnm (1−u)n−m um ,

ступенчатая функция δ(u) может быть аппроксимирована следующими полиномами:

w0 (u) = 0 b1, 0 (u) +1 b1, 1(u),

w1(u) = 0 b3,0 (u) +0 b3,1(u) +1 b3,2 (u) +1 b3,3 (u),

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

wk (u) = 0 b2k+1,0 (u) + +0 b2k+1,k +1 b2k+1,k+1(u) + +1 b2k+1,2k+1(u),

где k {0,1, ...}. Удаляя нулевые слагаемые из приведенных выше формул, получим следующие выражения для этих полиномов:

153

2k+1

wk (u) = ∑ b2k+1,i (u),

i=k+1

где k {0, 1, ...}, а u [0, 1]. Назовем полиномы wk (u) полиномами, сгла-

живающими ступенчатую функцию или просто сглаживающими полиномами. В геометрических приложениях наиболее часто используются следующие полиномы, сглаживающие ступенчатую функцию:

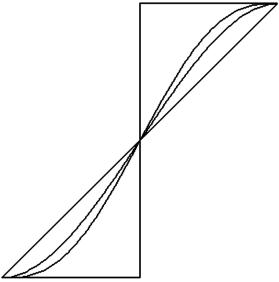
w0 (u) = u ,

w1(u) = 3(1−u)u2 +u3 ,

w2 (u) =10(1−u)2 u3 +5(1−u)u4 +u5 .

Профили этих сглаживающих полиномов показаны на рис. 7.2.

Рис. 7.2. Профили сглаживающих полиномов

Из определения сглаживающих полиномов следует, что они удовлетворяют следующим граничным условиям:

wk (0) = 0, wk (1) =1,

wk(l) (0) = wk(l) (1) = 0.

для всех l {1, ..., k}. Кроме того, эти полиномы обладают следующими

свойствами.

Свойство 1. Сглаживающие полиномы удовлетворяют следующему тождеству:

154

wk (u) + wk (1−u) =1

для любых k {0, 1, ...} и любых значений u [0, 1].

Доказательство. Как было показано в разделе 7.1, полиномы Бернштейна имеют следующие свойства:

n

∑bn,m (u) =1,

m=0

bn,m (1−u) = bn,n−m (u).

Учитывая эти свойства и подставив в определение сглаживающего полинома вместо u значение (1−u), получим

i=0

Свойство доказано.

Свойство 2. Сглаживающие полиномы wk (u) симметричны относительно точки u =1/ 2 для любых k {0,1, ...}.

Доказательство. Из свойства 1 следует, что wk (u) + wk (1−u) =1

для любых k {0, 1, ...} и любых значений u [0, 1]. Положим,

u= 12 +v,

иподставим это значение в равенство из свойства 1, получим

wk (1/ 2 +v) + wk (1/ 2 −v) =1

для любого значения v [−1/ 2, 1/ 2], что и означает симметричность полиномов wk (u) относительно точки u =1/ 2.

Свойство доказано.

155

Свойство 3. Сглаживающие полиномы удовлетворяют равенству

1/ 2

klim→∞ ∫0 wk (u)du = 0.

Доказательство. Очевидно, что полиномы wk (u) могут быть пред-

ставлены в степенном базисе uk+1, uk +2 , …, u2k +1. Следовательно, неопределенный интеграл от полинома wk (u) будет полиномом в степенном

базисе uk +2 , uk+3, …, u2k +2. На нижнем пределе интеграла этот полином равен нулю. Если перейдем в этом полиноме к пределу при k → ∞ на верхнем пределе интеграла, то также получим значение ноль. Отсюда и следует данное свойство.

Свойство доказано.

Из свойств 2 и 3 следует, что при повышении степени полином wk (u) неограниченно близко приближается к ступенчатой функции δ(u), что также можно наблюдать на рис. 7.2.

Свойство 4. Для любого значения k {0, 1, ...} полином wk (u) является минимумом функционала

1

Jk+1( f ) = ∫| f (k +1) (u) |2 du,

0

где функция f (u), u [0, 1], удовлетворяет следующим граничным условиям:

f (0) = 0, f (1) =1, f (l) (0) = f (l) (1) = 0

для любого l {1, 2, ..., k}.

Доказательство. Пусть функция g(u) является минимумом функционала Jk +1( f ). Рассмотрим функцию

(g − wk )(u) = g(u) − wk (u) .

Тогда

| (g − wk )(k+1) |2 =| g(k+1) − wk(k +1) |2 =

=(g(k+1) )2 − 2g(k+1)wk(k+1) +(wk(k+1) )2 =

=(g(k+1) )2 −(wk(k +1) )2 −2(g(k+1) − wk(k+1) )wk(k+1).

156

Из полученного уравнения следует, что

1

Jk+1(g − wk ) = Jk+1(g) − Jk+1(wk ) − 2∫(g(k +1) (u) − wk(k +1) (u))wk(k+1) (u)du.

0

Этот интеграл может быть вычислен по частям следующим образом:

1 1

∫(g(k +1) (u) − wk(k+1) (u))wk(k+1) (u)du = ∫wk(k+1) (u)d (g(k ) (u) − wk(k ) (u)) =

1

= −∫(g(k ) (u) − wk(k ) (u))wk(k+2) (u)du,

0

учитывая, что

Применяя эту рекуррентную формулу для последовательного интегрирования по частям и учитывая, что функция wk(2k+1) (u) является константой, получим

1 1

∫(g(k +1) (u) − w(k+1) (u))w(k+1) (u)du = (−1)k ∫(g′(u) − wk′−1(u))w(2+k+1) (u)du =

k k k 1 0 0

= (−1)k ((g(u) − wk−1(u))wk(2k +1) (u)) 10 = 0,

так как

g(0) = wk (0) = 0, g(1) = wk (1) =1.

Таким образом, доказано, что

Jk +1(g − wk ) = Jk+1(g) − Jk+1(wk ).

Последнее равенство может быть записано следующим образом:

Jk +1(g) = Jk +1(wk ) + Jk+1(g − wk ).

Из определения функционала Jk+1( f ) следует, что

Jk +1(g − wk ) ≥ 0.

Следовательно, выполняется неравенство

Jk+1(wk ) ≤ Jk +1(g).

157

Но функция g(u) является минимум функционала Jk+1( f ) по предположению, следовательно

g(u) = wk (u).

Таким образом, доказано, что полином wk (u) является минимумом функ-

ционала Jk +1( f ).

Докажем, что этот минимум является единственным. Предположим противное, что существует такая функция g(u), которая удовлетворяет

условию

Jk+1(g) = Jk+1(wk ).

Из этого уравнения следует, что

Jk +1(g − wk ) = 0

или другими словами

g(k +1) (u) = wk(k+1) (u)

для всех u [0, 1]. Следовательно,

k

g(u) = wk (u) +∑aiui.

i=0

Но коэффициенты ai для всех i {0, 1, ..., k} равны нулю, учитывая граничные условия, которым должна удовлетворять функция g(u). Следовательно,

g(u) = wk (u),

что и требовалось доказать. Свойство доказано.

Свойство 4 показывает, что полиномы wk (u) аппроксимируют ступен-

чатую функцию оптимальным образом относительно k +1 производной. Например, полином w1(u) является минимумом функционала энергии

J2 ( f ). Это не является неожиданным, так как аналогичным свойством обладают кубические сплайны.

7.6. Дифференцирование сглаживающих полиномов

Найдем формулу для вычисления производных от сглаживающих полиномов wk (u), где k {0, 1, ...}. Используя формулу (7.4), производная

порядка l от полинома wk (u) может быть определена следующим образом:

158

для любого значения l {1, 2, ..., k}. Производные от сглаживающих полиномов wk (u) имеют следующие свойства.

Свойство 1. Для любых значений l {0, 1,…, k} выполняется равенство

wk(l) (u) = (−1)l+1 wk(l) (1−u),

где k {0, 1, ...}.

Доказательство. Это свойство следует из свойства 1, доказанного в разделе 7.5.

Свойство 2. Производные полиномов wk (u), где k N, удовлетворяют следующим граничным условиям

wk(l) (0) = wk(l) (1) = 0

для всех l {1, ..., k}.

Доказательство. Из свойства 1 следует, что сглаживающие полиномы wk (u) , где k {0, 1, ...}, удовлетворяют следующему равенству:

wk(l) (0) = (−1)l+1 wk(l) (1).

С другой стороны, из построения полиномов wk (u) следует, что при k N выполняется равенство

wk(l) (0) = 0

для всех l {1, ..., k}. Из двух этих равенств следует, что

wk(l) (0) = wk(l) (1) = 0

для всех l {1, ..., k}.

Свойство доказано.

Пример. Рассмотрим сглаживающий полином w2 (u) =10(1−u)2 u3 +5(1−u)u4 +u5 .

Найдем первые две производные этого полинома. Получим

159