Pobegailo

w2′(u) = 30(1−u)2 u2 ,

w2′′(u) = 60(1−u)2 u −60(1−u)u2 .

Теперь найдем значения этих производных в граничных точках. Получим w2′(0) = w2′(1) = 0, w2′′(0) = w2′′(1) = 0.

7.7. Деформация однопараметрических групп Ли

Рассмотрим произвольную мультипликативную группу G. Обозначим через g1(u) и g2 (u), где u [0, 1], некоторые однопараметрические под-

группы группы G, которые удовлетворяют следующим начальным условиям:

где e обозначает единичный элемент группы G. Проблема состоит в том, чтобы построить такую однопараметрическую подгруппу g(u) G, где

u [0, 1], которая удовлетворяет следующим граничным условиям:

для всех l {1, 2, ..., k}, где k N. В этом случае подгруппа g(u) будет называться деформацией однопараметрических подгрупп g1(u) и g2 (u).

Другими словами можно сказать, что однопараметрическая группа g(u)

гладко деформируется или переходит из однопараметрической подгруппы g1(u) в однопараметрическую подгруппу g2 (u). Для решения этой

проблемы используем сглаживающие полиномы wk (u), которые были

определены в разделе 7.5. А именно, при помощи этих полиномов определим для однопараметрических подгрупп g1(u) и g2 (u) новую параме-

тризацию, о чем и говорится далее. Определим для k N полиномы

учитывая граничные условия, которым удовлетворяют полиномы wk (u). Определим производные по параметру u от полиномов τ−k (u). Получим

160

(τ−k (u))′ = −wk′(u)u +(1− wk (u)),

(τ−k (u))′′ = −wk′′(u)u − wk′(u) − wk′(u) = −wk′′(u)u − 2wk′(u), (τ−k (u))′′′ = −wk′′′(u)u − wk′′(u) − 2wk′′(u) = −wk′′′(u)u −3wk′′(u)

и, следовательно,

(τ−k (u))(l) = −wk(l) (u)u −lwk(l−1) (u),

где l {2, 3, ..., k}. Из этих равенств следует, что производные от полиномов τ−k (u) удовлетворяют следующим граничным условиям:

для всех l {2, 3, ..., k}, учитывая свойство 2 из раздела 7.6. Профили некоторых полиномов τ−k (u) показаны на рис. 7.3.

Рис. 7.3. Профили первых трех полиномов τ−k (u)

учитывая граничные условия, которым удовлетворяют полиномы wk (u). Определим производные по параметру u от полиномов τ+k (u), получим

(τ+k (u))′ = wk′(u)u + wk (u),

(τ+k (u))′′ = wk′′(u)u + wk′(u) + wk′(u) = wk′′(u)u +2wk′(u), (τ+k (u))′′′ = wk′′′(u)u + wk′′(u) + 2wk′′(u) = wk′′′(u)u +3wk′′(u)

и, следовательно,

161

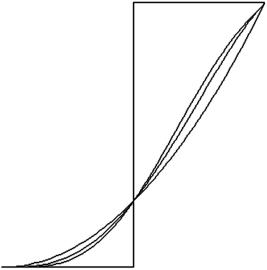
(τ+k (u))(l) = wk(l) (u)u +lwk(l−1) ,

где l {2, 3, ..., k}. Из этих равенств следует, что производные от полиномов τ+k (u) удовлетворяют следующим граничным условиям:

для всех l {2, 3, ..., k}, учитывая свойство 2 из раздела 7.6. Профили некоторых полиномов τ+k (u) показаны на рис. 7.4.

Рис. 7.4. Профили первых трех полиномов τ+k (u)

Следующая теорема показывает, как с помощью полиномов τ−k (u) и

τ+k (u) можно выполнить гладкий переход между однопараметрическими

группами Ли.

Теорема. Если g1(u) и g2 (u), где u [0, 1], являются такими однопа-

раметрическими подгруппами группы G, которые удовлетворяют равенствам (7.16), то однопараметрическая подгруппа

где u [0, 1], удовлетворяет граничным условиям, заданным равенствами

(7.17) и (7.18).

Доказательство. Пусть g1(u) и g2 (u), где u [0, 1], будут такими однопараметрическими подгруппами группы G, которые удовлетворяют

162

равенствам (7.16). Рассмотрим однопараметрическую подгруппу g(u), которая определена равенством (7.27). Здесь полиномы τ−k (u) и τ+k (u) определены равенствами (7.19) и (7.24). Из определения подгруппы g(u) следует, что она удовлетворяет следующим граничным условиям:

g(0) = g2 (τ+k (0))g1(τ−k (0)) = g2 (0)g1(0) = g1(0),

g(1) = g2 (τ+k (1))g1(τ−k (1)) = g2 (1)g1(0) = g2 (1),

принимая во внимание равенства (7.16), (7.20) и (7.25). Следовательно, граничные условия, заданные равенствами (7.17), выполняются.

Производные по параметру u от подгрупп g1(τ−k (u)) и g2 (τ+k (u)) можно определить следующими рекуррентными формулами:

g1(l) (τ−k (u)) = (g1(l−1) )′τ−k (τ−k (u))′, g2(l) (τ+k (u)) = (g2(l−1) )′τ+k (τ+k (u))′,

где l N. Так как производные полиномов τ−k (u) и τ+k (u) удовлетворяют

граничным условиям, заданным соответственно равенствами (7.21), (7.22), (7.25), (7.26), то из последних двух равенств следует, что произ-

l

g(l) (u) = ∑Cli (g2 (τ+k (u)))(i) (g1(τ−k (u)))(l−i)

i=1

163

для l N. Отсюда следует, принимая во внимание равенства (7.28)– (7.31), что производные по параметру u от подгруппы g(u) удовлетво-

ряют следующим граничным условиям:

g(l) (0) = g1(l) (0), g(l) (1) = g2(l) (1)

для l {1, 2, ..., k}. В результате получили, что граничные условия, за-

данные равенствами (7.18), также выполняются. Теорема доказана.

7.8. Сглаживание однопараметрических групп Ли

Рассмотрим произвольную мультипликативную группу Ли G. Обозначим через g1(1−u) и g2 (u), где u [0, 1], некоторые однопараметри-

ческие подгруппы группы G, которые удовлетворяют следующим начальным условиям:

где e обозначает единичный элемент группы G. Проблема состоит в том, чтобы построить такую однопараметрическую подгруппу g(u) G, где

u [0, 1], которая удовлетворяет следующим граничным условиям:

для всех l {1, 2, ..., k}, где k N. В этом случае подгруппа g(u) будет называться сглаживанием однопараметрических подгрупп g1(u) и g2 (u).

Другими словами можно сказать, что однопараметрическая группа g(u) гладко сглаживает точку соединения однопараметрических подгрупп g1(u) и g2 (u). Для решения этой проблемы используем сглаживающие полиномы wk (u), которые были определены в разделе 7.5. А именно, при по-

мощи этих полиномов определим для однопараметрических подгрупп g1(u) и g2 (u) новую параметризацию, о чем и говорится далее.

Определим для k N полиномы

164

учитывая граничные условия, которым удовлетворяют полиномы wk (u). Определим производные по параметру u от полиномов σ−k (u). Получим

(σ−k (u))′ = −wk′(u)(1−u) −(1− wk (u)),

(σ−k (u))′′ = −wk′′(u)(1−u) + wk′(u) + wk′(u) = −wk′′(u)(1−u) + 2wk′(u), (σ−k (u))′′′ = −wk′′′(u)(1−u) + wk′′(u) +2wk′′(u) = −wk′′′(u)(1−u) +3wk′′(u)

и, следовательно,

(σ−k (u))(l) = −wk(l) (u)(1−u) +lwk(l−1) ,

где l {2, 3, ..., k}. Из этих равенств следует, что производные от полиномов σ−k (u) удовлетворяют следующим граничным условиям:

для всех l {2, 3, ..., k}, учитывая свойство 2 из раздела 7.6. Графики некоторых полиномов σ+k (u) показаны на рис. 7.5.

Рис. 7.5. Графики некоторых полиномов σ+k (u)

165

учитывая граничные условия, которым удовлетворяют полиномы wk (u). Производные по параметру u от полиномов σ+k (u) имеют те же значения на границах интервала [0, 1], что и производные по параметру u от полиномов τ+k (u), определенных в предыдущей главе, а именно:

рис. 7.3, так как полиномы σ+(u) совпадают с полиномами τ+k (u). Следующая теорема показывает, как с помощью полиномов σ−k (u) и

σ+k (u) можно выполнить гладкое сглаживание однопараметрических групп Ли.

Теорема. Если g1(1−u) и g2 (u) , где u [0,1] , являются такими одно-

параметрическими подгруппами группы G, которые удовлетворяют равенствам (7.32), то однопараметрическая подгруппа

где u [0, 1], удовлетворяет граничным условиям, заданным равенствами

(7.33) и (7.34).

Доказательство. Пусть g1(1−u) и g2 (u) , где u [0, 1], будут такими однопараметрическими подгруппами группы G, которые удовлетворяют равенствам (7.32). Рассмотрим однопараметрическую подгруппу g(u),

которая определена равенством (7.43). Здесь полиномы σ−k (u) и σ+k (u) определены равенствами (7.35) и (7.39). Из определения подгруппы g(u) следует, что она удовлетворяет следующим граничным условиям:

g(0) = g2 (σ+k (0))g1(σ−k (0)) = g2 (0)g1(1) = g1(1), g(1) = g2 (τ+k (1))g1(τ−k (1)) = g2 (1)g1(0) = g2 (1),

принимая во внимание равенства (7.32), (7.36) и (7.40). Следовательно, граничные условия, заданные равенствами (7.33), выполняются.

Производные по параметру u от подгрупп g1(σ−k (u)) и g2 (σ+k (u)) можно определить следующими рекуррентными формулами:

166

g1(l) (σ−k (u)) = (g1(l−1) )′σ−k (σ−k (u))′, g2(l) (σ+k (u)) = (g2(l−1) )′σ+k (σ+k (u))′,

где l N. Так как производные полиномов σ−k (u) и σ+k (u) удовлетворяют

граничным условиям, заданным соответственно равенствами (7.37), (7.38) и (7.41), (7.42), то из последних двух равенств следует, что произ-

для l {1, 2, ..., k}.

для l N. Отсюда следует, принимая во внимание равенства (7.44)–(7.47), что производные по параметру u от подгруппы g(u) удовлетворяют сле-

дующим граничным условиям:

для l {1, 2, ..., k}. В результате получили, что граничные условия, задан-

ные равенствами (3.34), также выполняются. Теорема доказана.

Глава 8

МОДЕЛИРОВАНИЕ СПЛАЙН-КРИВЫХ НА СФЕРЕ S2

В этой главе рассмотрен подход к моделированию сплайн-кривых на поверхности двумерной сферы при помощи деформации и сглаживания параметрических поворотов. В следующей главе этот же подход будет использован для моделирования ориентационных кривых. Отметим, что изучение данной главы существенно упростит понимание материала, изложенного в следующей главе.

Представленный в данной главе материал, организован следующим образом. Сначала рассмотрено построение интерполяционных сплайнкривых, а затем сглаживание углов ломаных линий на поверхности двумерной сферы. Сегменты сплайн-кривых определяются как деформации дуг окружностей, являющихся орбитами поворотов.

Отметим, что изложенный подход можно рассматривать как кинематический способ построения сплайн-кривых. Потому это особенно подходит для решения различных кинематических задач, например таких, как планирования траекторий роботов.

Другие подходы к моделированию кривых на поверхности двумерной сферы рассмотрены в работах [52–64].

8.1. Постановка задачи построения сплайн-кривой на сфере

Рассмотрим сферу S 2 , которая описана каноническим уравнением

x2 + y2 + z2 = r2

относительно некоторой ортогональной системы координат с началом в центре этой сферы. Пусть задана некоторая последовательность различ-

предполагается, что последовательность содержит более трех точек, т. е. k > 3.

168

Проблема формулируется следующим образом:

1. Нужно построить параметризованную кривую r(t), которая лежит на поверхности сферы S 2 и проходит через точки Pi для всех i {1,2,…,k}. В этом случае говорят, что параметризованная кривая r(t) интерполирует точки Pi.

2. Параметризованная кривая r(t) должна принадлежать классу Cn , т. е. иметь непрерывные производные до порядка n включительно.

3. Дополнительным требованием к параметризованной кривой r(t)

является ее инвариантность относительно выбора ортогональной системы координат с началом в центре сферы.

Параметризованная кривая r(t), удовлетворяющая перечисленным выше требованиям, будет называться интерполяционным сплайном на

поверхности сферы S 2.

Предлагаемое решение этой проблемы, которое рассматривается в дальнейших разделах 8.2–8.4, базируется на деформации дуг малых ок-

ружностей сферы S2 , каждая из которых проходит через три соседние точки последовательности (P1, P2, ..., Pk ).

8.2. Построение дуг малых окружностей по точкам

Рассмотрим сферу S 2 , которая описана каноническим уравнением

x2 + y2 + z2 = r2

относительно ортогональной системы координат с началом в центре сферы. Возьмем три различные точки P1 , P2 и P3 на поверхности сферы S 2.

В этом случае эти точки определяют секущую плоскость, которая описывается уравнением

ответственно. Раскрывая определитель, это уравнение может быть переписано следующим образом:

169