Способы задания операций.

Так как операция является функцией, то для ее задания применимы любые спо­собы задания функций, перечисленные в предыдущем пара­графе. Приведем некоторые наиболее употребляемые спосо­бы представления унарных и бинарных операций.

1. Способы задания унарных операций φ: М → Мна конечном множествеМ ={… ,}

• Перечнем всех аргументов аизМ(для частично определенной операции - из ее области определенияφМ) и соответствующих им значенийb, a, bM, представленных строкой

φ= (→,→, ... ,→),

а чаще парой строк:

φ= .

В случае, если предварительно зафиксирован список (последовательность) элементов (а,а,...,а)множестваМ, то для задания операцииφдостаточно указать вектор значений (b, b,..., b). При этомφ(а) =b, т.е. результат выполнения операцииφдляi-го аргумента списка равенi-й компонен­те вектора значений.

• Списком всех пар "аргумент-значение" (а, b) φ, а,b М, для всех возможных значений аргументов:

φ ={(),(),...,()}.

Число таких пар |прφ | =m М=n.

• Формулой φ(а) = b, напримерlg а = b.

2. Способы задания бинарных операций φ:М × М Мна конечном множествеМ={}:

Таблица Кэли

• Таблицей Кэли- для чего слева и сверху таблицы выписы­ваются все значения аргументоваиbиз множестваМсоответственно, а на пересечении строки, соответствующей аргументуа, и столбца, соответствующего аргументуb, записывается ре­зультат с операцииφнад аиb. На рис. 5.2. приведена таблица Кэли для операции, называемой "сложением по модулю 3" на множествеМ = {0, 1, 2}и обозначаемой "mod3", или(результат с выполнения операцииравен остатку от деления суммы аргументов(а + b)на З ).

	0 1 2
0 1 2	0 1 2 1 2 0 2 0 1

Рис. 5.2.

Списком всех троек (а, b, с), гдеа,b- соответственно первый и второй аргументы из М, с-результат выполнения операции φнад аиb,a,b,c M. Для всюду определенной операции число всех троек в списке

|M×M|= . Например, для операции сложения по модулю 3:

={(0,0,0), (0,1,1), (0,2,2), (1,0,1), (1,1,2), (1,2,0), (2,0,2), (2,1,0), (2,2,1)}.

• Формулой φ (а, b) = с- так называемоепрефиксноепред­ставление операции; иное -инфиксное- представление бинарной операции формулойa φ b = c, например,а b= с, где - операция сложения по модулю 3.

Тема 6. Алгебраическая система. Гомоморфизмы. Проверка условия гомоморфизма. Изоморфизмы. Изоморфные алгебры. Изоморфизм модели. Примеры изоморфных алгебр. Алгебраическая система

Определение 6.1.Множество Μ вместе с заданными на нем операциями {φ1, φ2,...,φ n} называется алгеброй. Обозначение алгебры:, где М называется основным множеством (несущим множеством, носителем), а - сигнатурой алгебры A.

Примером алгебры является полугруппа - множество Μ с заданной на нем одной бинарной ассоциативной операцией (обозначается: · ), т.е. A= {М; ·}, например множество натуральных чисел N с операцией сложения + на нем, т.е. A= {Ν; +} является полугруппой.

Типом алгебры A называется вектор парностей операций сигнатуры. Например, в алгебре A= {R; +, χ}, где R - множество действительных чисел, + и χ - соответственно операции сложения и умножения (такая алгебра называется полем действительных чисел), сигнатура Σ = {+, χ} включает две бинарные операции - сложение и умножение. Поэтому тип данной алгебры (2,2).

Определение 6.2.Алгебраическую систему, где множествосостоит из одной двухместной операции, называется группоидом.

Определение 6.2. кольцом называется алгебра с двумя операциями, если обладает следующими свойствами:

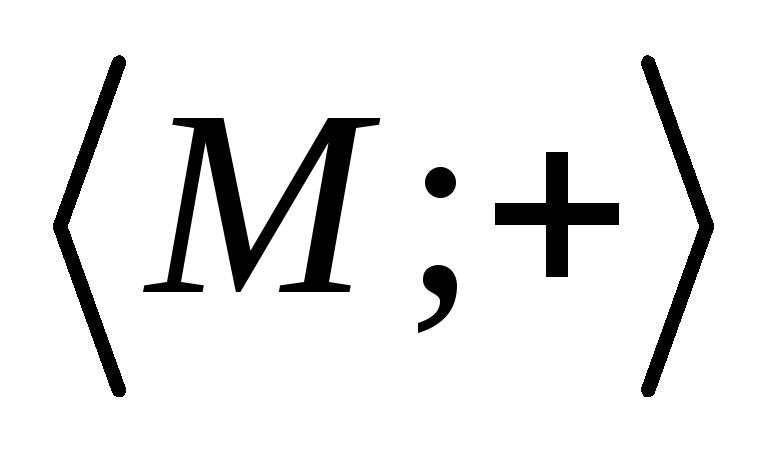• - Авелева группа

• - полугруппа

• Операция умножения дистрибутивна относительно сложения ().

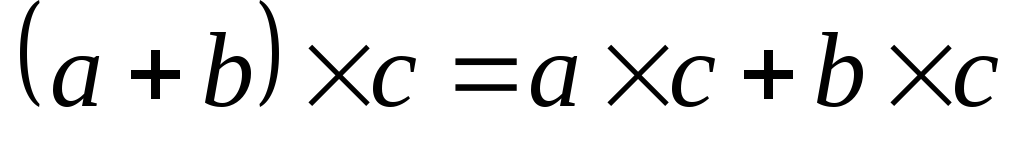Определение 6.3.Множество Μ вместе с заданными на нем отношениями {R₁ R₂, ..., R_n} называется моделью. Обозначение модели: , где М - несущее множество (универсум), – сигнатура модели V. Например, моделью V₁| является мно­жество М₁, чисел с отношениями: "быть больше" (>) и "быть равным" (=), т.е. V₁ = (M₁; >, =), или некоторое множество M_г людей с отношением R - "быть руководителем", т.е. V_г = (М₂; R), и т.д.

Определение 6.4.Множество Μ вместе с заданными на нем операциями {φ₁, φ₂, ..., _n} и отношениями {R_1, R₂, ···,R_n} называется алгебра­ической системой, или алгебраической структурой. Обозначение алгебраической структуры:

V= (Μ; φ₁, φ₂,..., φ_n; R₁, R₂,..., R_n).

Если полугруппа обладает коммутативным свойством (), то её называют Авелевой группой.

Примером алгебраической структуры является так назы­ваемая решетка - множество Μ с заданными на нем: одним бинарным отношением частичного порядка (обозначение ≤) и двумя бинарными операциями ( ∩ и U ): {М;≤; ∩, U }.

Таким образом, алгебры - это алгебраические структуры с пустым множеством отношений. Другим частным случаем алгебраических структур являются модели, т.е. множества, на которых заданы только отношения.