Представление кратчайших путей в алгоритме
Часто
требуется не просто подсчитать веса
кратчайших путей, но и найти сами эти
пути. Пусть G
= (V, E) - заданный
граф. Для каждой вершины
будем
помнить её предшественника
.
Предшественик вершины - это либо другая
вершина, либо NIL. По завершении работы
алгоритмов цепочка предшественников
, начинающаяся с произвольной вершины
v ,
будет представлять собой кратчайший
путь из s
в v
, так что, если
≠
NIL, процедура Print-Path(G,s,v)
напечатает кратчайший путь из s
в v.
До завершения работы алгоритмов цепочки, получаемые итерациями π, не обязательно будут кратчайшими путями, но всё равно можно рассмотреть ориентированный подграф предшествования Gπ = (Vπ , E π ), определенный так: вершины Gπ - это те вершины G, у которых предшественник отличен от NIL, плюс исходная вершина:
Vπ= {v
V
: π [v] ≠ NIL}
{s}
. Рёбра Gπ- это стрелки, указывающие из π [v] ≠ NIL вv:
Eπ= {(π [v], v)
E
:v
Vπ
\ {s}}
.
Дерево кратчайших путей с корнем в s есть ориентированный подграф G´ = (V´, E´),
где
V ´
V и E
´
E , для
которого:
V ´- множество вершин, достижимых из вершиныs,
G ´является деревом с корнемs,
для каждого v
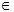V
´путь изsвvв графеG ´является кратчайшим путем изsвvв графеG .
Алгоритм Флойда
Алгоритм Флойда находит кратчайшие пути между всеми парами вершин (узлов) в (ор)графе. В этом алгоритме для хранения информации о путях используется матрица Н: array [1..p,1..p] of 1..p, где
Алгоритм Флойда
Вход: матрица С[1..p,1..p] длин дуг.
Выход: матрица Т[1..p,1..p] длин путей и матрица Н[1..p,1..p] самих путей
for i from 1 to p do
for j from 1 to p do
T[i,j]:=C[i,j] {инициализация}
if C[i,j]=∞ then
H[i,j]:=0 {нет дуги из i в j}
else
H[i,j]:=j {есть дуга из i в j}
end if
end for
end for
for i from 1 to p do
for j from 1 to p do
for k from 1 to p do
if i≠j & T[j,i]≠∞ & i≠k & T[i,k]≠∞ & (T[j,k]=∞VT[j,k]>T[j,i]+T[i,k])
then
H[j,k]:=H[j,i] {запомнить новый путь}
T[j,k]:=T[j,i]+T[i,k] {и его длину}
end if
end for
end for
for j from 1 to p do
if T[j,j]<0 then
stop {нет решения: вершина j входит в цикл отрицательной длины}
end if
end for
end for
Матрица H размера О(р2) хранит информацию обо всех (кратчайших) путях в графе. Заметим, что всего в фафе О(р2) путей, состоящих из О(р) вершин. Таким образом, непосредственное представление всех путей потребовало бы памяти объема О(р3). Экономия памяти достигается за счет интерпретации представления, то есть динамического вычисления некоторой части информации вместо её хранения в памяти. В данном случае любой конкретный путь <u,v> легко извлекается из матрицы с помощью следующего алгоритма.
w:=u; yield {первая вершина}
while w≠u do
w:=H[w,u]; yield w {следующая вершина}
end while
Если в G есть цикл с отрицательным весом, то решения поставленной задачи не существует, так как можно «накручивать» на этом цикле сколь угодно короткий путь.
Алгоритм Флойда имеет много общего с алгоритмом Уоршала. Покажем по индукции, что после выполнения i-го шага основного цикла по i элементы матриц T[j,k] и H[j,k] содержат, соответственно, длину кратчайшего пути и первую вершину на кратчайшем пути из вершины j в вершину k, проходящем через промежуточные вершины из диапазона 1..i. База: i=0, то есть до начала цикла элементы матриц T и H содержат информацию о кратчайших путях (если таковые есть), не проходящих ни через какие промежуточные вершины. Пусть теперь перед началом выполнения тела цикла на i-том шаге T[j,k] содержит длину кратчайшего пути от j к k, а H[j,k] содержит первую вершину на кратчайшем пути из вершины j в вершину k (если таковой есть). В таком случае, если в результате добавления вершины i к диапазону промежуточных вершин находится более короткий путь (в частности, если это вообще первый найденный путь), то он записывается. Таким образом после окончания цикла, когда i=p, матрицы содержат кратчайшие пути, проходящие через промежуточные вершины 1..p, то есть искомые кратчайшие пути. Алгоритм не всегда выдает решение, поскольку он не всегда существует. Дополнительный цикл по j служит для прекращения работы в случае обнаружения в графе цикла с отрицательным весом.