Связность.

Определение 10.5.Говорят, что две вершины связаны, если существует соединяющая их простая цепь.

Определение 10.6.Граф, в котором все вершины связаны – называют связным.

Отношение связанности вершин является эквивалентностью. Классы эквивалентности по отношению связанности называют компонентами связности графов. Число компонентов графа Gобозначаютk(G). ГрафGявляется связным тогда и только тогда, когдаk(G) = 1. Еслиk(G) > 1, тоG– несвязный граф. Граф, состоящий только из изолированных вершин, в которомk(G) =p(G) иr(G) = 0 называют вполне несвязным графом.

Виды графов: тривиальные и полные графы, двудольные графы, орграфы и сети.

Определение 10.7.Граф, состоящий из одной вершины называется тривиальным.

Определение 10.8. Граф у которого любая пара вершин смежные называется полным графом.

Полный граф с Р вершинами обозначается k_p. Его максимальное количество ребер находится по формуле.

Пример.

.

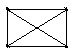Действительно, можно заметить, что данный граф имеет 6 ребер.

Определение 10.9. Полный подграф некоторого графа называется кликой этого графа.

Граф, состоящий из простого цикла с kвершинами обозначается с_k.

Определение 10.10.Двудольным графом (биграфом, чётным графом) называется такой графG(V,E), что, при чём всякое ребро из множестваЕ инцидентно вершине изV₁и вершине изV₂. Множество изV₁иV₂называется долями этого графа

Определение 10.11.Если двудольный граф содержит все ребра, соединяющие множестваV₁иV₂, то такой граф называют полным двудольным графом.

Теорема.Граф является двудольным тогда и только тогда, когда все его простые циклы имеют четную длину.

Определение 10.11.Если в графе ориентировать все ребра, то получится направленный орграф.

Определение 10.12.Если в графе полустепень захода некоторой вершины равна 0 (d⁺=0), то такая вершина называется источником.

Определение 10.13.Если в графе полустепень исхода некоторой вершины равна 0 (d^-=0), то такая вершина называется стоком.

Определение 10.13.Направленный граф с одним истоком и одним стоком называется сетью.

Тема 11. Матрица смежности, матрица инцидентности. Операции над графами. Представление графов в эвм. Матрица смежности. Матрица инцедентности.

Определение 11.1.Представление графа с помощью квадратной матрицы, отражающей смежность вершин М: array[1..p,l..p]of[0..1]называется матрицей смежности, где

М[i,j] =

Определение 11.2.Представление графа с помощью матрицыH: array[1..p, 1..q]of[0..1], отражающей инцидентность вершин и ребер, называетсяматрицей инциденций.

Для неориентированного графа:

H[i,j] =

Для ориентированного графа используют матрицу Н: array[1..p, 1..p]of[-1..1]

H[i,j] =

Операции над графами позволяют образовывать новые графы из нескольких более простых. В этом параграфе будут рассмотрены операции на графах без параллельных ребер (дуг).

Операции над графами: Объединение графов.

Пусть G₁(X₁,E₁)иG₂(X₂,E₂)– произвольные графы.

Определение 11.3.Объединением G₁G₂ графовG₁иG₂называется граф с множеством вершинX₁X₂, и с множеством ребер (дуг) E₁E_2.

Рассмотрим операцию на примере графов G₁(X₁,E₁)иG₂(X₂,E₂), приведенных на рис. 11.1. Множества вершин первого и второго графов соответственно равныX₁ = {x₁, x₂, x₃}иX₂ = {x₂, x₃, x₄}, а множество вершин результирующего графа определится какX = X₁X₂ = {x₁, x₂, x₃, x₄}. Аналогично определяем множества дуг графа:

E₁ = {(x₁, x₂), (x₁, x₃), (x₂, x₁), (x₃, x₃)}. E₂ = {(x₂, x₄), (x₃, x₂)_, (x₄, x₂)}.

E = {(x₁, x₂), (x₁, x₃), (x₂, x₁), (x₃, x₃), (x₂, x₄), (x₃, x₂)_, (x₄, x₂)}.

Результирующий граф G(X,E) = G₁(X₁,E₁)G₂(X₂,E₂) также приведен на рис. 11.1.

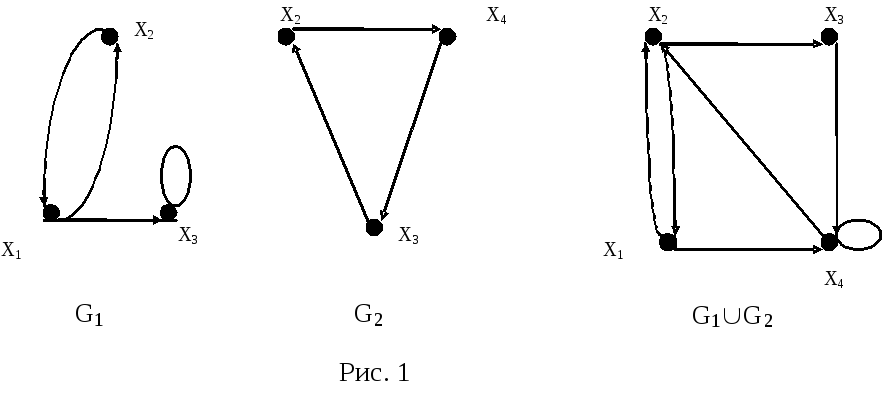
Рисунок 11.1

Операция объединения обладает следующими свойствами, которые следуют из определения операции и свойств операций на множествах:

0. G₁G₂ = G₂G₁– свойство коммутативности;

1. G₁(G₂G₃) = (G₁G₂)G₃– свойство ассоциативности.

Операция объединения графов может быть выполнена в матричной форме. Для графов с одним и тем же множеством вершин справедлива следующая теорема.

Теорема 11.2. ПустьG₁иG₂– два графа (ориентированные или не ориентированные одновременно) с одним и тем же множеством вершинX, и пустьA₁иA₂– матрицы смежности вершин этих графов. Тогда матрицей смежности вершин графаG₁G₂ является матрицаA = A₁A₂, образованная поэлементным логическим сложением матрицA₁иA₂.

Рассмотрим выполнение операции объединения графов, множества вершин которых не совпадают. Пусть G₁(X₁,E₁)иG₂(X₂,E₂)– графы без параллельных ребер и множестваX₁иX₂вершин этих графов не совпадают. ПустьA₁иA₂– матрицы смежности их вершин графов. Для таких графов операция объединения может быть выполнена следующим образом.

В соответствии с определением операции объединения графов найдем множество вершин результирующего графа как X₁X₂. Построим вспомогательные графыG’₁и G’₂, множества вершин которых есть множествоX₁X₂, а множество ребер (дуг) определяется множествамиE₁для графаG^’₁иE₂для графаG^’₂. Очевидно, что матрицыA’₁иA’₂смежности вершин этих графов могут быть получены из матрицA₁иA₂путем добавления в них дополнительных столбцов и строк с нулевыми элементами.

Применив к графам G’₁иG’₂теорему 4.1, найдем матрицу смежности вершин графаG’₁G’₂какA’₁A’₂. Очевидно, что полученной матрице смежности вершин соответствует граф, множество вершин которого равноX₁X₂, а множество ребер определяется, какE₁E₂, что соответствует операции объединения графов.

Пример.Выполнить в матричной форме операцию объединения графовG₁иG₂, представленных на рис. 1.

Составим матрицы смежности вершин графов.

			x1	x2	x3				x2	x3	x4
		x1	0	1	1			x2	0	0	1
A1	=	x2	1	0	0	A2	=	x3	1	0	0
		x3	0	0	1			x4	0	1	0

Множество вершин результирующего графа X₁X₂ = {x₁, x₂, x₃, x₄}. Составим матрицы смежности вершин вспомогательных графовG’₁и G’₂.

			x1	x2	x3	x4				x1	x2	x3	x4
		x1	0	1	1	0			x1	0	0	0	0
A’1	=	x2	1	0	0	0	A’2	=	x2	0	0	0	1
		x3	0	0	1	0			x3	0	1	0	0
		x4	0	0	0	0			x4	0	0	1	0

Матрица A = A’₁A’₂ имеет вид

			X1	x2	x3	x4
		x1	0	1	1	0
		x2	1	0	0	1
A = A’1A’2	=	x3	0	1	1	0
		x4	0	0	1	0

Полученная матрица смежности вершин A’₁  A’₂соответствует графуG₁G₂, изображенному на рис.11.1.