Теорема Форда - Фалкерсона. Алгоритм нахождения максимального потока.

Теорема: На любой сети максимальная величина потока из истокаSв стокtравна минимальной пропускной способности разреза, отделяющегоSотt. Т.е. существует такой поток по сети:M*G =max∑Mi=minC(A/B).

Алгоритм нахождения максимального потока:1)Построить некоторый начальный потокX0 = {X0ij}. В примере это потоки М1 и М2. 2)Организовать процедуру составления подмножества А вершин, достижимых из истокаSпо ненасыщенным ребрам. А={s, 3, 2,t}. Если в этом процессе стокtне попадает в подмножество А, то построенный поток максимальный и задача решена, если же стокtпопал в А, то перейти к пункту 3 алгоритма.3)Выделить путь из истокаsв стокt, состоящий из ненасыщенных ребер и увеличить поток Хijпо каждому ребру этого пути на величину ∆=min(Cij-Xij), гдеminберется поi-тымj-тым ребрам этого пути. Тем самым будет построен поток и затем следует вернуться к пункту 2 алгоритма. ( Мы построили М3 ). А={1}, В={2, 3, 4, 5}.R*(A/B)=6.

Тема 14. Кратчайшие пути. Алгоритм Флойда. Алгоритм Дейкстры.

Если задан орграф G(V,E), в котором дуги помечены числами и эти числа обычно называют весами или длинами, то орграф можно представить в виде матрицы весов.

_{||Cij|| =}

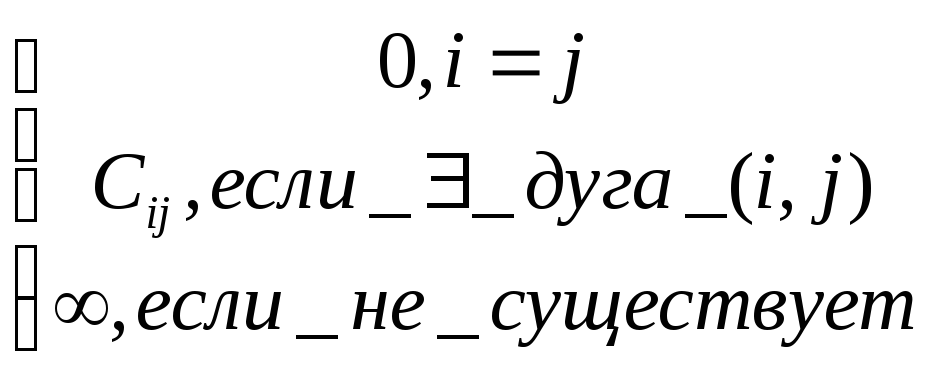
Длиной пути называется сумма длин дуг, входящих в этот путь. Наиболее часто на практике встречается задача отыскания кратчайшего пути. Алгоритм Флойда находит все кратчайшие пути между всеми парами вершин в орграфе. Алгоритм ДХ3 находит кратчайший путь между двумя данными вершинами орграфа, если длины дуг неотрицательны.

Кратчайшие пути

Ориентированный граф G = (V, E) состоит из множества вершин V и множества дуг E. Вершины также называют узлами, а дуги – ориентированными ребрами. Дуга представима в виде упорядоченной пары вершин (v, w), где вершина v называется началом, а w – концом дуги.

Неориентированный граф G = (V, E) состоит из конечного множества вершин V и множества ребер E. В отличие от ориентированного графа, здесь каждое ребро (v, w) соответствует неупорядоченной паре вершин: если (v, w) – неориентированное ребро, то (v, w) = (w, v).

Вершина Х называется инцидентной ребру G, если ребро соединяет эту вершину с какой-либо другой вершиной.

В задаче о кратчайшем пути нам дан ориентированный взвешанный граф G = (V, E) с вещественной весовой функцией w: E R

Вес пути p=(v₀,v₁,...,v_k) - это сумма весов рёбер, входящих в этот путь:

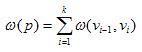
Вес кратчайшего пути из u в v равен, по определению,

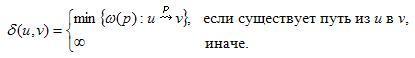
Кратчайший путь из u в v - это любой путь p из u в v, для которого

Граф называется вырожденным, если у него нет рёбер.

Вершины называются смежными, если существует ребро, их соединяющее.

Пустым называется граф без рёбер. Полным называется граф, в котором каждые две вершины смежные.

Цикл, в котором все вершины, кроме первой и последней, попарно различны, называется простым циклом.

Граф называется связным, если для любых двух вершин существует путь, соединяющий эти вершины.

Рёбра отрицательного веса

Иногда веса ребер могут быть отрицательными. При этом важно, есть ли циклы отрицательного веса. Если из вершины s можно добраться до цикла отрицательного веса, то потом можно обходить этот цикл сколь угодно долго, и вес будет всё уменьшаться, так что для вершин этого цикла кратчайших путей не существует:

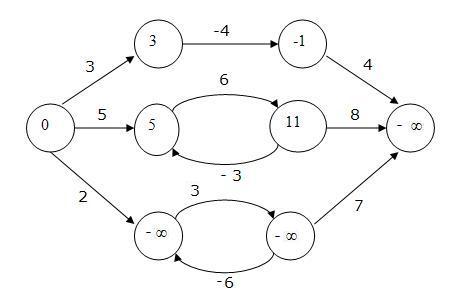
В таком случае можно считать, что вес кратчайшего пути есть −∞.

Если же циклов отрицательногов веса нет, то любой цикл можно выбросить не удлиняя пути. Путей без циклов конечное число, так что вес кратчайшего пути корректно определен.