Сложность алгоритма

Сложность алгоритма Дейкстры зависит от способа нахождения вершины v, а также способа хранения множества непосещенных вершин и способа обновления меток. Обозначим через n количество вершин, а через m — количество ребер в графе G.

• В простейшем случае, когда для поиска вершины с минимальным d[v] просматривается все множество вершин, а для хранения величинd— массив, время работы алгоритма естьO(n²+m). Основной цикл выполняется порядкаnраз, в каждом из них на нахождение минимума тратится порядкаnопераций, плюс количество релаксаций (смен меток), которое не превосходит количества ребер в исходном графе.

• Для разреженных графов (то есть таких, для которых m много меньше n²) непосещенные вершины можно хранить в двоичной куче, а в качестве ключа использовать значения d[i], тогда время извлечения вершины из станет logn, при том, что время модификацииd[i] возрастет до logn. Так как цикл выполняется порядка n раз, а количество релаксаций не больше m, скорость работы такой реализацииO(nlogn+mlogn)

• Если для хранения непосещенных вершин использовать фибоначчиеву кучу, для которой удаление происходит в среднем за O(logn), а уменьшение значения в среднем заO(1), то время работы алгоритма составитO(nlogn+m). Однако, согласно сайту intuit.ru,

скрытые константы в асимптотических оценках трудоемкости велики и использование фибоначчиевых куч редко оказывается целесообразным: обычные двоичные (d-ичные) кучи на практике эффективнее.

Альтернативами им служат толстые кучи, тонкие кучи и кучи Бродала, обладающие теми же асимптотическими оценками, но меньшими константами.

Тема 15. Свободные деревья. Основные свойства деревьев. Ориентированные, упорядоченные и бинарные деревья. Представление в ЭВМ свободных, ориентированных и упорядоченных деревьев.

Свободные деревья. Основные свойства деревьев.

Деревья заслуживают отдельного и подробного рассмотрения по двум причинам.

Деревья являются в некотором смысле простейшим классом графов. Для них вы-полняются многие свойства, которые не всегда выполняются для графов в общем случае. Применительно к деревьям многие доказательства и рассуждения оказываются намного проще. Выдвигая какие-то гипотезы при решении задач теории графов, целесообразно сначала их проверять на деревьях.

Деревья являются самым распространенным классом графов, применяемых в про-граммировании, причем в самых разных ситуациях. Более половины объема этой главы посвящено рассмотрению конкретных применений деревьев в программировании.

Свободные деревья.Изучение деревьев целесообразно начать с самых общих определений и установления основных свойств. Граф без циклов называетсяациклическим, или лесом. Связный ациклический граф называется (свободным)деревом. Таким образом, компонентами связности леса являются деревья.Замечание:Прилагательное "свободное" употребляется в том случае, когда нужно подчеркнуть отличие деревьев от других объектов, родственных деревьям: ориентированных деревьев, упорядоченных деревьев и т. д.

В связном графе Gвыполняется неравенствоq(G)p(G) – 1. ГрафG,в которомq(G) =p(G) – 1, называетсядревовидным. В ациклическом графеG z(G) = 0 Пустьи, v —несмежные вершины графаG, х= (u,v) E.Если графG + химеет только один простой цикл,z(G + х) =1, то графGназываетсясубциклическим.

Пример:

На рисунке показаны диаграммы всех различных (свободных) деревьев с 5 вер­шинами.

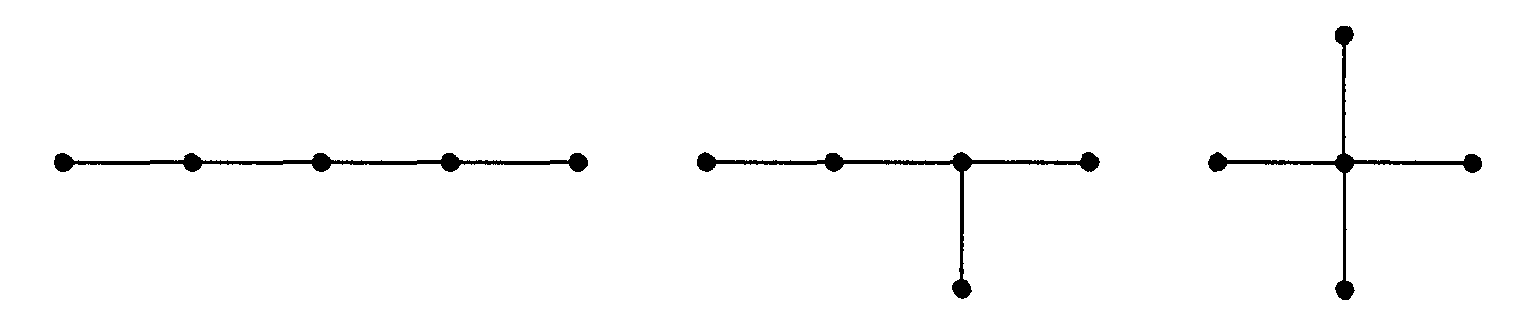
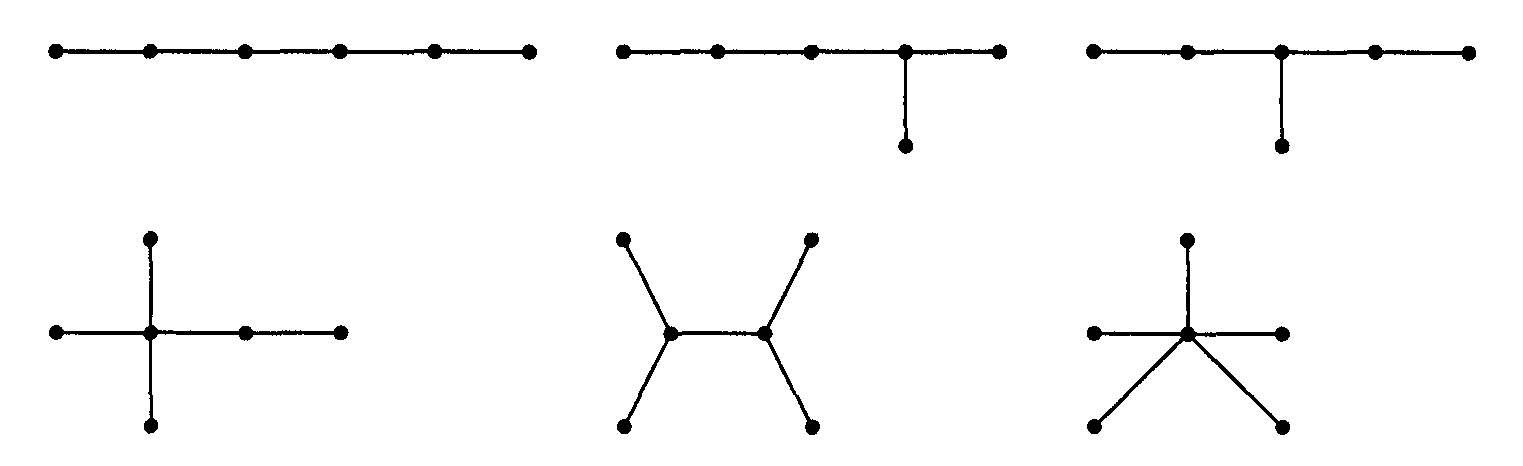
На рисунке - диаграммы всех различных (свободных) деревьев с 6 вершинами

Основные свойства деревьев.Следующая теорема устанавливает, что два из четырех свойств – связность, ацикличность, древовидность и субцикличность – характеризуют граф как дерево.

Теорема: ПустьG(V,Е) – граф с р вершинами,qребрами,kкомпонентами связности иzпростыми циклами. Пусть далеех– ребро, соединяющее любую пару несмежных вершин в графеG, тогда следующие утверждения эквивалентны:

1. Граф G- дерево, то есть связный граф без цикловk(G) = 1 &z(G) = 0 ;

2. Любые две вершины соединены в G единственной простой цепью: G: u,v  ! <u, v>;

3. Граф G - связный граф, и любое ребро есть связный мостG: k(G) = 1 & e  Ek(G – e) > 1;

4. Граф G- связный и древовидныйG: k(G) = 1 & q(G) =p(G) – 1;

5. Граф G- ациклический и древовидныйG: z(G) = 0 & q(G) =p(G) – 1;

6. Граф G- ациклический и субциклическийG:z(G) = 0 &z(G+x) = 1;

7. Граф G- связный, субциклический и неполный.

Следствие: В любом нетривиальном дереве имеются по крайней мере две висячие вершины.