Тема 9. Основное определение графов. Смежность. Изоморфизм графов. Элементы графов. Подграфы. Валентность. Теорема Эйлера. Основное определение.
Среди дисциплин и методов дискретной математики теория графов и особенно алгоритмы на графах находят наиболее широкое применение в программировании
Теория графов многократно переоткрывалась разными авторами при решении различных прикладных задач.
1. Задача о Кенигсбергских мостах. Обойти все четыре части суши, пройдя по каждому мосту один раз, и вернуться в исходную точку (рис. 9.1(а)). Эта задача была решена Эйлером (1707-1783) в 1736 году.
2. Задача о трех домах и трех колодцах. Имеется три дома и три колодца. Провести от каждого дома к каждому колодцу тропинку так, чтобы тропинки не пересекались (рис. 9.1(б)). Эта задача была решена Куратовским (1896-1979) в 1930 году.
3. Задача о четырех красках. Любую карту на плоскости раскрасить четырьмя красками так, чтобы никакие две соседние области не были закрашены одним цветом (рис. 9.1(в)).
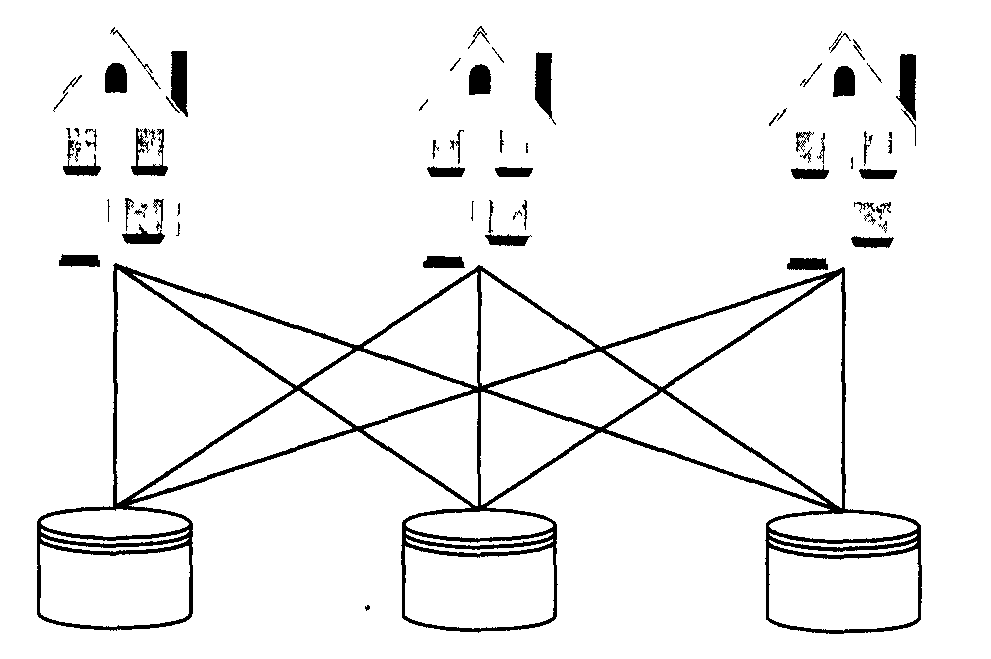
а) б) в)
Рисунок 9.1.
Определение 9.1.ГрафомG(V,E) называется совокупность двух множеств – непустого множестваV(множества вершин) и множестваEнеупорядоченных пар различных элементов множестваV(E– множество ребер).G(V,E)=<V,E>,V≠,EVV,E=E-1. Число вершин графаGобозначимр, а число ребер —q:p:=p(G):=|V|,q:=q(G):=|E|.
Определение 9.2. Пусть ν1, ν2 — вершины,e= (ν1, ν2) – соединяющее их ребро. Тогда вершина νiи реброe инцидентны, вершина ν2и реброeтакже инцидентны. Два ребра, инцидентные одной вершине, называются смежными, две вершины, инцидентные одному ребру, также называются смежными.
Смежность.
Определение 9.3. Множество вершин, смежных с вершиной ν, называется множеством смежности вершины ν и обозначается Г+(ν): Г+(ν):={uV| (u,v)E}, Г(ν):=Г.
Часто рассматриваются следующие родственные графам объекты: 1)Если элементами множестваЕявляютсяупорядоченныепары, то граф называетсяориентированным(илиорграфом).В этом случае элементы множестваVназываютсяузлами,а элементы множестваЕ-дугами. 2)Если элементом множестваЕможет быть параодинаковых(не различных) элементовV,то такой элемент множестваЕназываетсяпетлей,а граф называетсяграфом с петлями(илипсевдографом ).3)ЕслиЕявляется не множеством, анабором,содержащим несколько одинаковых элементов, то эти элементы называютсякратными ребрами,а граф называетсямультиграфом.4)Если элементами множестваЕявляются не обязательно двухэлементные, алюбыеподмножества множестваV,то такие элементы множестваЕназываютсягипердугами,а граф называетсягиперграфом.5)Если задана функцияР: V Ми/илиР: Е М,то множествоМназывается множествомпометок,а граф называетсяпомеченным(илинагруженным). В качестве множества пометок обычно используются буквы или целые числа.
Далее выражение "граф G{V,Е}" означает неориентированный непомеченный граф без петель и кратных ребер.
Изоморфизм графов.
Определение 9.4. Говорят, что два графаG1(V,Е) иG2(V,Е) - изоморфны(обозначаетсяG1~G2), если существует биекцияН:V1V2, сохраняющая смежностьe1=(u, v)E1. Из этого и наличия биекции следует, чтое2(h(u),h(v))E2. Изоморфизм графов есть отношение эквивалентности. Действительно, изоморфизм обладает всеми необходимыми свойствами:
1) рефлексивностьG1~G2,где требуемая биекция есть тождественная функция,
2) симметричностьеслиG1~G2с биекциейh,тоG2~G1 с биекциейh-1,
3) транзитивностьеслиG1~G2 с биекциейhиG2~G3 с биекциейg,тоG1~G3с
биекцией hg.
Графы рассматриваются с точностью до изоморфизма,то есть рассматриваются классы эквивалентности по отношению изоморфизма.
Пример:
Три внешне различные диаграммы являются диаграммами одного и того же графа:
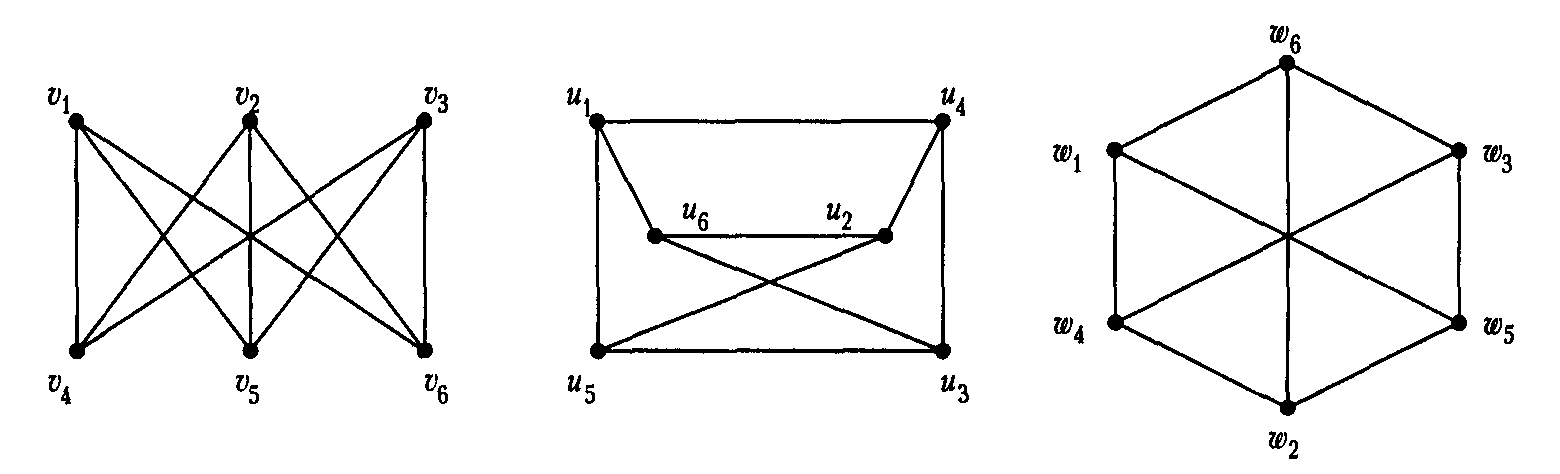
Определение 9.5. Числовая характеристика, одинаковая для всех изоморфных графов, называетсяинвариантомграфа. Так,р(G) иq(G) — инварианты графаG. Неизвестно никакого набора инвариантов, определяющих граф с точностью до изоморфизма
Пример:
Количество вершин, ребер и количество смежных вершин для каждой вершины не определяют граф. Ниже представлены диаграммы графов, у которых указанные инварианты совпадают, но графы при этом не изоморфны
