Тема 4. Замыкание отношений. Транзитивное замыкание, рефлексивное замыкание. Алгоритм Уоршалла вычисления транзитивного замыкания. Замыкание отношений.

Замыканием отношения R относительно свойства P называется такое множество R*, что:

1. RR*.

2. R^*обладает свойствомP.

3. R^*является подмножеством любого другогоотношения, содержащегоRи обладающего свойствомP.

Замыкание является весьма общим математическим понятием. Неформально говоря, замкнутость означает, что многократное выполнение допустимых шагов не выводит за определенные границы.

Пример

Пусть на множестве A={1,2,3,4} задано отношениеR={(1,2),(3,4),(4,2)}. Видно, что отношениеRнесимметрично, нерефлексивнои нетранзитивно. ЗамыканиемRотносительно свойства симметричности являетсяR^*={(1,2),(3,4),(4,2);(2,1),(4,3),(2,4)}. ЗамыканиемRотносительно рефлексивности являетсяR^*={(1,2),(3,4),(4,2);(1,1),(2,2),(3,3),(4,4)}. ЗамыканиемRотносительно транзитивности является множествоR^*={(1,2),(3,4),(4,2);(3,2)}.

Транзитивное замыкание отношений

Определение 4.1. Отношение называется транзитивным замыканием отношения, определенного на множествеM, тогда и только тогда, когда существуют такие, что.

Пример

На множестве Nопределено отношение. Тогда транзитивное замыкание этого отношения для значений 1<2<…<6 будет отношение 1<6. (Рисунок 4.1)

Рисунок 4.1

Транзитивным замыканием отношения «быть сыном» является отношение «быть прямым потомком».

Транзитивным замыканием отношения «иметь общую стену» для жильцов одного дома является отношение « жить на одном этаже».

Пример.ПустьRзадано наM,.R транзитивно, если для любых a,b,с из аRb и bRс следует аRс. В матрице такого отношения должно выполняться следующее условие: если в i-й строке стоит единица, например в j-й координате (столбце) строки, т.е. , товсем единицам в j-й строке (пусть этим единицам соответствуют k-е координаты такие, что ) должны соответствовать единицы в i-й строке в тех же k-х координатах, т.е. (и, может быть, еще и в других координатах). Это условие иллюстрируется на рисунке 4.2, где кружком выделена единица , для которой производится проверка условия, а стрелками показана последовательность проверки данного условия.

В матрице транзитивного отношения это условие должно выполняться для любых таких, что . И наоборот, если в матрице R имеется хотя бы одна единица , для которой данное условие не выполняется, то R не транзитивно.

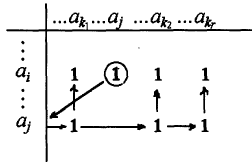
Рисунок 4.2

Рефлексивное замыкание отношений

Пусть тождественное отношение Е состоит из упорядоченных пар самого себя – . Тогда R*=RE (R* – рефлексивное замыкание, а R – транзитивное замыкание).

Если R транзитивно и рефлексивно, то R*=R.

Пример. Используя R – отношение на N такое, что получим.

Алгоритм Уоршалла.

Вход:отношение, заданное матрицей R.

Выход:транзитивное замыкание отношения, заданное матрицей Т.

S := R

for i from 1 to n do

for j from 1 to n do

for k from 1 to n do

T[j, k] := S[j, k] V S[j, i] & S[i, k]

end for

end for

S := T

end for

Заметим, что нас не интересует число путей любой конкретной длины из вершины v_iв вершину v_j. Эта информация, получаемая в процессе вычисления степеней A, далее игнорируется. Для того, чтобы сократить объем вычислений, можно отказаться от получения указанной информации и использовать в вычислениях просто реализуемые булевские матричные операции, которые мы определим согласно.

Обозначим булевскую сумму C двух матриц A и B размера n*n как С=АВ, а булевское произведение –D=AB.

Элементы матриц C и D задаются соотношениями

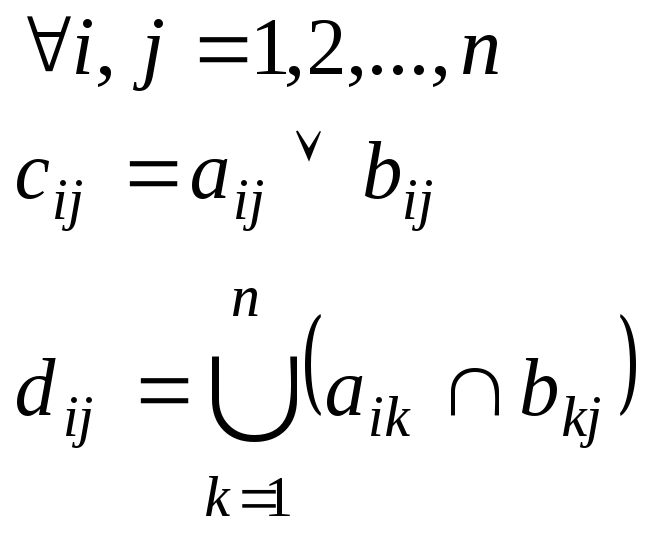
Заметим, что элемент d_ijлегко получается путем просмотра i-й строки матрицы A слева направо и одновременно j-го столбца матрицы B сверху вниз. Если k-й элемент в строке матрицы A и k-й элемент в столбце матрицы B равны 1 для какого-нибудь k, то d_ij=1. В противном случае d_ij=0.

Булевы матрицы более экономичны в вычислительном отношении, чем целочисленные. Действительно, запоминание булевой матрицы требует меньшего объема оперативной памяти ЭВМ по сравнению с целочисленной матрицей той же размерности. Кроме того, выполнение на компьютере логических операций над булевыми матрицами требует меньшего объема вычислений, чем над целочисленными матрицами тех же размерностей.

Матрица смежностей, так же как и путевая матрица, является булевской матрицей. Заметим, что .

Единственная разница между A²и A⁽²⁾заключается в том, что A⁽²⁾является булевской матрицей и элемент на пересечении i-й строки и j-го столбца A⁽²⁾равен 1 в том случае, когда существует по крайней мере один путь длины 2 из v_iв v_j. Аналогичное положение имеет место для A³и A⁽³⁾и в общем случае для A^rи A^(r)при любом целом положительном r. Из этих рассуждений ясно, что матрица достижимости P задается выражением

Например, если

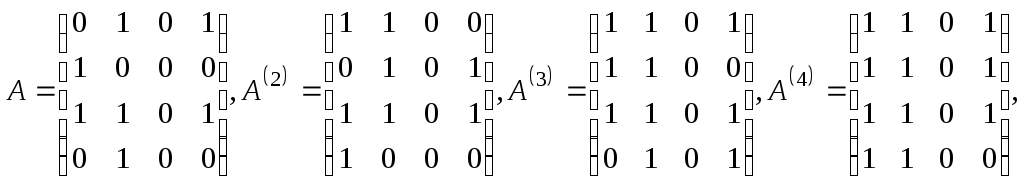то

Данный метод получения матрицы достижимости ориентированного графа называется алгоритмом Уоршалла (Warshall S.A. A Theorem on Boolean Matrices. - J.ACM, 1962, 9, pp.11-12).

Тема 5. Функции и отображения. Инъекция, сюръекция, биекция. Представление функций в ЭВМ. Операции. Свойства бинарных операций: ассоциативность, коммутативность, дистрибутивность слева и справа. Способы задания операций. Таблица Кэли.

Функции и отображения. Инъекция, сюръекция, биекция.

Понятие “функции” является одним из основополагающих в математике, в данном случае подразумевается прежде всего функции, отображающие одно конечное множество объектов в другое конечное множество, мы избегаем использование термина “отображение” и предпочитаем слово “функция” в расчете на постоянное сопоставление читателем математического понятия функции с понятием функции в языках программирования .

Определения 5.1.Говорят, что между множествамиАиВопределено соответствиеГ, если задано некоторое произвольное подмножество декартового произведения .

Определения 5.2.Отображением множества А на множество В называется такое соответствие, которое каждому элементу сопоставляется по крайней мере один элемент. Тогда элементb называется образом элемента а, a a – прообразом элемента b, или переменной, или аргументом.

Определения 5.3. Соответствие, при котором каждомуаАсопоставляется один и только один элементbB, ,называется функциональным соответствием, илифункцией изАвВ, и обозначается следующим образом или .

Если b=f(a) , тоаназываютаргументом, аb–значением функции.

Замечание.

Вообще всякому отношению RизAв В можно сопоставить (тотальную) функцию (эта функция называетсяхарактеристической функцией отношения), полагая

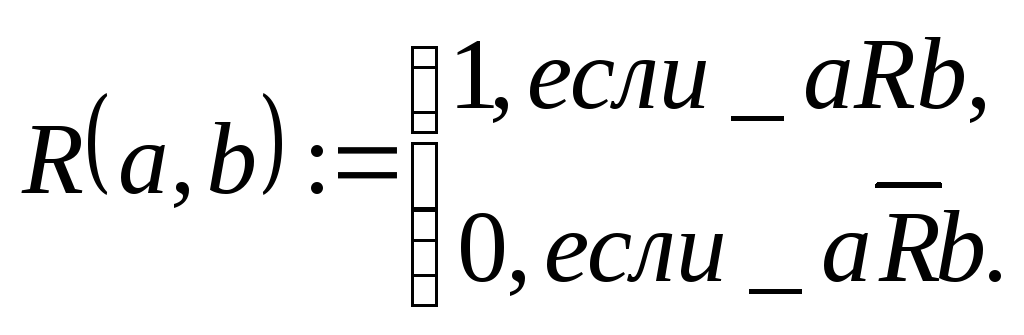
Пусть , тогда

Область определения функции:.

Область значения функции:.

Определения 5.4. Если,то функция называетсятотальной, а если, то –частичной.

Определения 5.5. Суждением функциина множественазывается функция, определяемая следующим образом:.

Для тотальной функции .

Определения 5.6. Функцияназывается функциейnаргументов, илиn-местнойфункцией.

Инъекция, сюръекция и биекция.

Пусть . Тогда функция является:

Инъективной, или инъекцией, если.

Сюръективной, или сюръекцией, если.

Биективной, или биекцией, если она инъективная и сюръективная.

Замечание.

Биективную функцию также называют взаимно однозначной.

Рис.5.1. иллюстрирует понятия отношения, функции, инъекции, сюръекции и биекции.

Рисунок 5.1.

Теорема.

Если – тотальная биекция (), то отношение(обратная функция) является биекцией.

Доказательство.

Поскольку – биекция, имеем

.

Покажем, что – функция.

Поскольку .

Тогда .

Покажем, что – инъекция. Пусть.

Тогда . Покажем от противного, что– сюръекция.

Пусть . Тогда. Обозначим этот элемент. Имеем:.

Индуцированная функция.

Пусть и пусть. Тогда множество

называется образом множества, а множество–прообразоммножества. Заметим, чтоFявляется отношением из множествав множество.

Теорема.

Если –функция, то и– тоже функции

Замечание.

называется индуцированной функцией, а -переходам к прообразам.