Минимальный каркас. Схема алгоритма построения минимальных каркасов.

Задача отыскания минимального каркаса (кратчайшего остова) – классическая задача теории графов. Методы решения этой задачи послужили основой многих других важных результатов (исследование алгоритма Краскала привели к созданию теории "жадных" алгоритмов).

Пусть G(V,E) – граф. Остов (каркас) –остовнойподграф, являющийся деревом. Несвязный граф не имеет остова, связный граф может иметь много остовов. Если задать длины ребер, то можно поставить задачу нахождения кратчайшего остова, или минимального каркаса.

Пример:Пример практической интерпретации задачи нахождения кратчайшего остова. Пусть задано множество аэродромов, и нужно определить минимальный по сумме расстояний набор авиарейсов, который позволил бы перелетать с любого аэродрома на любой другой аэродром. Решение задачи – кратчайший остов полного графа расстояний между аэродромами.

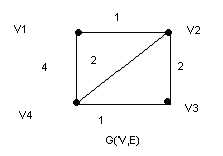
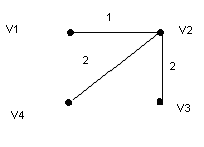
Граф расстояний между аэродромами и дерево кратчайших путей из вершины v1.

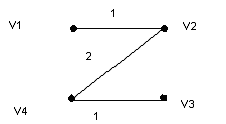
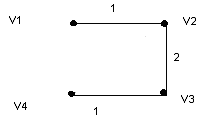
Кратчайшие остовы для графа G(V,E)

Рассмотрим схему алгоритма построения кратчайшего остова. Пусть Т – множество непересекающихся деревьев, являющихся подграфами графа G. Вначале Т состоит из отдельных вершин графаG, в конце Т содержит единственный элемент – кратчайший остов графаG.Схема алгоритма.

Вход:графG(V,E), заданный матрицей длин ребер С.

Выход:кратчайший остов Т.

Т:=V

whileв Т больше одного элементаdo

взять любое поддерево из Т

найти к нему ближайшее

соединить эти деревья в Т

end while

Тема 17. Циклы и коциклы. Эйлеровы циклы. Гамильтоновы циклы. Теорема Дирака. Раскраска графов. Хроматическое число. Планарные графы. Укладка графов. Алгоритм раскрашивания.

21. Циклы и коциклы. Эйлеровы циклы. Гамильтоновы циклы. Теорема Дирака.

Цикл может входить только в одну компоненту связности графов.

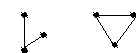
k(G)=2

Следовательно, далее будем рассматривать связанные графы. Цикл (простой) рассматривается как множество рёбер. Разрез связного графа – это множество ребер, удаление которых делает граф не связным.

е₁

е₃

С₃:

С₃ –{e₁, e₂}→k(G’)=2

Простой разрез – это минимальный разрез, т.е. такой, никакое собственное подмножество которого разрезом не является. Между циклами и разрезами существует определенная двойственность. Следовательно, разрезы называют коциклами. Чем больше в графе циклов, тем труднее его разрезать. В дереве, напротив, каждое ребро является разрезом. Максимальное независимое множество циклов – это фундаментальная система циклов. Циклы фундаментальной системы называются фундаментальными, а количество циклов в данной фундаментальной системы – циклическим рангом, или циклическим числом. Обозначение: m(G). Максимальное независимое множество коциклов (разрезов) – фундаментальная система разрезов. Коциклы фундаментальной системы – фундаментальные, а количество коциклов в данной фундаментальной системе называетсяк-циклическим рангом, или коциклическим числом графаG. Обозначение:m^*(G).

Пусть T(V,ET) – остов графаG(V,T). КодеревоT^*(V,ET^*) остоваT(V,GT) – такой подграф (остовный), чтоET^* =E/ET. Кодерево не является деревом. Ребра кодерева – хорды остова.

Теорема 1. Если граф G – связный граф, то цикломатическое число определяется как:m(G) =q-p+ 1, а коцикломатическое – как:m^*(G) =p- 1.

Если граф имеет цикл (не обязательно простой), содержащий все ребра графа по одному разу, то это Эйлеров цикл, а граф – Эйлеров граф. Если граф имеет цепь (не обязательно простую), содержащую все вершины по одному разу, то цепь – Эйлерова цепь, а граф – полуэйлеров граф. Эйлеров цикл содержит не только все ребра (по одному разу), но и все вершины графа (возможно по несколько раз). Эйлеровым может быть только связный граф.

Теорема 2. Если граф G связен и не тривиален, то справедливы следующие утверждения:1)Граф G – Эйлеров граф;2)Каждая вершина графа G имеет четную степень.3)Множество ребер графа G можно разбить на простые циклы.

Чтобы убедится в наличии Эйлерова цикла, в графе необходимо и достаточно проверить, что степени всех вершин четные.

эйлеров граф

Если граф имеет простой цикл, содержащий все вершины графа по одному разу, то такой цикл – Гамильтонов, а граф – Гамильтонов граф. Гамильтонов цикл не обязательно содержит все ребра графа. Гамильтоновым может быть только связный граф.

Теорема 3(теорема Дирака). Если в графеG(V,E) для любой вершиныuиз множестваVd(u)іp/ 2, то графG– Гамильтонов.

гамильтонов граф