Раскраска графов. Хроматическое число. Планарность. Укладка графов. Алгоритмы раскрашивания.

Раскраска графов – приписывание цветов (например, чисел) его вершинам так, что никакие две смежные вершины не получают одинаковый цвет. Наименьшее возможное число цветов раскраски – хроматическое число. Обозначение:x(G). Очевидно, что существуетm-раскраска графаGдля любогоmв диапазонеx(G)mp. Множество вершин одного цвета - одноцветный класс. Одноцветные классы образуют независимые множества вершин, т. е. никакие две вершины в одноцветном классе не смежны.

Теорема 1.Хроматическое число графаGне превышает максимальной степени вершин графа, увеличенной на 1.x(G)1 +G.

Граф укладывается на некоторой поверхности, если его можно нарисовать на этой поверхности так, чтобы ребра графа при этом не пересекались. Граф – планарный, если его можно уложить на плоскость. Плоский граф – граф, уложенный на плоскости. Область, ограниченная ребрами в плоскости графа и не содержащая внутри себя вершин и ребер, – грань. Число граней плоского графа Gобозначаетсяr(G).

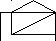
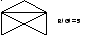
Планарный граф и его укладка на плоскости.

Внешняя часть плоскости также образует грань. Для графов, уложенных на некоторой поверхности, справедливо определенное соотношение между числом вершин, ребер и граней, это соотношение – Эйлерова характеристика поверхности.

Теорема 1(формула Эйлера). В связном планарном графе справедливо следующее:p-q+r= 2.

Теорема 2(о 5 красках). Всякий планарный граф можно раскрасить пятью красками.

Алгоритм раскрашивания: для раскрашивания графа применяют следующую схему рекурсивной процедуры p:

1)Выбрать в графеGнекоторое максимальное множество вершинS;

2)Покрасить вершины множестваSв очередной цвет;

3)Применить процедуруpк графуG –S.

Тема 18. Переключательные функции. Основные понятия и определения. Способы задания переключательных функций. Таблица истинности. Переключательные функции одного и двух аргументов. Специальные разложения ПФ.

Переключательные функции. Существенные и несущественные переменные. Булевы функции одной переменной. Булевы функции двух переменных.

Функции вида f :E₂ⁿE₂, гдеE₂= {0;1} – функции алгебры логики или булевы функции. Множество булевых функций отnпеременных обозначимp_nиp_n:= {f |f:E₂ⁿE₂}. Булеву функцию отnпеременных можно задать таблицей истинности.

x1	…	xn–1	xn	f(x1,…,xn)
0	…	0	0
0	…	0	1
0	…	1	0
…	…	…	…
1	…	1	1

Если число переменных n, то в таблице истинности имеется 2ⁿстрок, соответствующих всем различным комбинациям значений переменных, которым можно сопоставить 2^{2^n}различных столбцов, соответствующих различным функциям. Т.о. число булевых функций отnпеременных |p_n| = 2^{2^n}. Булева функцияf p_nсущественно зависит от переменнойx_i, если существует такой набор значенийa₁,a₂,…,a_i–1,a_i+1,…,a_n–1,a_n, что выполняется условиеf(a₁,a₂,…,a_i–1,a_i+1,…,a_n–1,a_n)f(a₁,a₂,…,a_i–1, 1,a_i+1,…,a_n–1,a_n). В этом случаеx_i– существенная переменная, в обратном случаеx_i– несуществующая (фиктивная) переменная.

Пример.Пусть булевы функцииf₁(x₁,x₂);f₂(x₁,x₂) заданы следующей таблицей истинности:

x1	x2	f1	f2
0	0	0	1
0	1	0	1
1	0	1	0
1	1	1	0

Для этих функций переменная x₁ – существенная, аx₂ – несущественная. По определению булевы функции равны, если одна из другой получается введением (или удалением) несущественных переменных.

Функции называются эквивалентными, если их таблицы совпадают с точностью до переменных.

Для исключения фиктивной переменной удаляется столбец с этой переменной, дублирующие строки удаляются.

Булевы функции одной переменной представим в виде таблицы.

Переменная x	f1(x)	f2(x)	f3(x)	f4(x)
0	0	0	1	1
1	0	1	0	1