Операция произведения графов.
Пусть G1(X,E1)иG2(Y,E2)- два графа.
Определение 11.7.ПроизведениемG1G2графовG1иG2называется граф с множеством вершинXY, а дуга из вершины(xi,yj)в вершину(xk,yl)существует тогда и только тогда, когда существуют дуги(xi,xk) E1и(yj,yl) E2.
Выполнение операции произведения рассмотрим на примере графов, изображенных на рис. 5. Множество вершин Zрезультирующего графа определяется как декартово произведение множествXY. МножествоZсодержит следующие элементы:z1=(x1y1), z2=(x1y2), z3=(x1y3), z4=(x2y1), z5=(x2y2), z6=(x2y3).
Определим множество дуг результирующего графа. Для удобства рассмотрения составим таблицу, в первом столбце которой указываются дуги графа G1,во втором – дуги графаG2, а в третьем и четвертом – дуги результирующего графа.
|
G1 |
G2 |
(x1,y1)(x2,y1) |
(z, z) |
|
(x1,x2) |
(y1,y1) (y1,y2) (y2,y3) (y3,y2) |
(x1,y1)(x2,y1) (x1,y1)(x2,y2) (x1,y2)(x2,y3) (x1,y3)(x2,y2) |
(z1,z4) (z1,z5) (z2,z6) (z3,z5) |
|
(x2,x1) |
(y1,y1) (y1,y2) (y2,y3) (y3,y2) |
(x2,y1)(x1,y1) (x2,y1)(x1,y2) (x2,y2)(x1,y3) (x2,y3)(x1,y2) |
(z4,z1) (z4,z2) (z5,z3) (z6,z2) |
Результирующий граф G1G2изображен на рис.11.5.
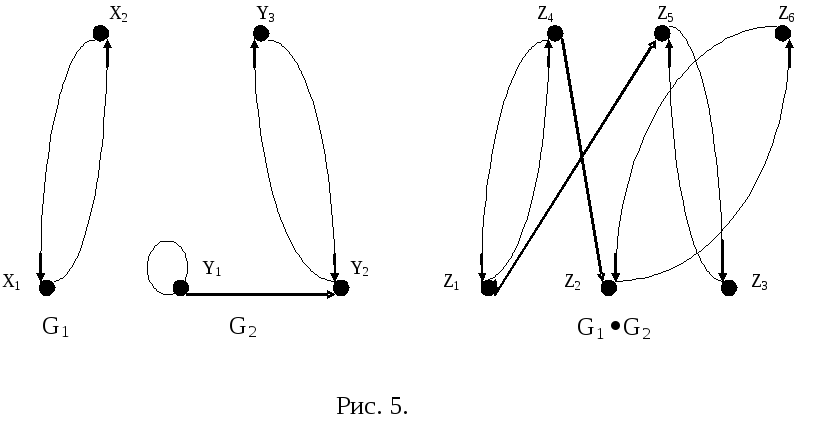
Рисунок 11.5.
Операция произведения обладает следующими свойствами.
1. G1G2 = G2G1.
2. G1(G2G3) = (G1G2)G3.
Рассмотрим выполнение операции произведения графов в матричной форме.
Пусть G1(X,E1)иG2(Y,E2)– два графа, имеющиеnx иny вершин соответственно. Результирующий графG1G2 имеетnxny вершин, а его матрица смежности вершин - квадратная матрица размером(nxny) (nx ny). Обозначим черезa =a(ij)(kl)элемент матрицы смежности вершин, указывающий на наличие дуги (ребра), соединяющей вершинуz=(xiyj)cz=(xkyl). Этот элемент может быть вычислен при помощи матриц смежности вершин исходных графов следующим образом:
a =a(ij)(kl) = a1,ik a2,jl, (3)
де a1,ik, a1,ik– элементы матрицы смежности вершин графовG1иG2 соответственно.
Пример.Выполнить операцию произведения на графах, приведенных на рис. 5.
Составим матрицы смежности вершин исходных графов.
|
|
|
|
x1 |
x2 |
|
|
|
y1 |
y2 |
y3 | |
|
|
|
x1 |
0 |
1 |
|
|
y1 |
1 |
1 |
0 | |
|
A1 |
= |
x2 |
1 |
0 |
A2 |
= |
y2 |
0 |
0 |
1 | |
|
|
|
|
|
|
|
|
y3 |
0 |
1 |
0 | |
Построим матрицу Aсмежности вершин результирующего графа, каждый элемент которой вычисляется согласно соотношению (4.3).
|
|
|
|
x1y1 |
x1y2 |
x1y3 |
x2y1 |
x2y2 |
x2y3 |
|
|
|
x1y1 |
a1,11 a2,11 |
a1,11a2,12 |
a1,11 a2,13 |
a1,12a2,11 |
a1,12 a2,12 |
a1,12 a2,13 |
|
|
|
x1y2 |
a1,11 a2,21 |
a1,11 a2,22 |
a1,11 a2,23 |
a1,12 a2,21 |
a1,12 a2,22 |
a1,12 a2,23 |
|
A |
= |
x1y3 |
a1,11 a2,21 |
a1,11 a2,22 |
a1,11 a2,23 |
a1,12 a2,31 |
a1,12 a2,32 |
a1,12 a2,33 |
|
|
|
x2y1 |
a1,21 a2,11 |
a1,21 a2,12 |
a1,21 a2,13 |
a1,22 a2,11 |
a1,22 a2,12 |
a1,22 a2,13 |
|
|
|
x2y2 |
a1,21 a2,21 |
a1,21 a2,22 |
a1,21 a2,23 |
a1,12 a2,21 |
a1,12 a2,22 |
A1,12 a2,23 |
|
|
|
x2y3 |
a1,21 a2,31 |
a1,21 a2,32 |
a1,21 a2,33 |
a1,22 a2,31 |
a1,12 a2,32 |
A1,12 a2,33 |
Для удобства рассмотрения разделим матрицу Aна четыре квадратные подматрицы. Заметим, что каждая подматрица может быть получена путем логического элементов матрицы умноженияA2на один из элементовa1,ij матрицыA1. С учетом этого матрицуA можно представить так:
|
|
|
|
x1y1 |
x1y2 |
x1y3 |
x2y1 |
x2y2 |
x2y3 |
|
|
|
x1y1 |
a1,11A2 |
a1,12A2 | ||||
|
|
|
x1y2 | ||||||
|
A |
= |
x1y3 | ||||||
|
|
|
x2y1 |
a1,21A2 |
a1,22A2 | ||||
|
|
|
x2y2 | ||||||
|
|
|
x2y3 | ||||||
Таким образом, матрица смежности вершин графа G1G2имеет вид:
|
|
|
|
x1y1 |
x1y2 |
x1y3 |
x2y1 |
x2y2 |
x2y3 |
|
|
|
x1y1 |
0 |
0 |
0 |
1 |
1 |
0 |
|
|
|
x1y2 |
0 |
0 |
0 |
0 |
0 |
1 |
|
A |
= |
x1y3 |
0 |
0 |
0 |
0 |
1 |
0 |
|
|
|
x2y1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
|
|
x2y2 |
0 |
0 |
1 |
0 |
0 |
0 |
|
|
|
x2y3 |
0 |
1 |
0 |
0 |
0 |
0 |
Нетрудно убедиться, что полученной матрице смежности вершин соответствует граф G1G2, представленный на рис. 11.5.