Основные характеристики нечетких множеств

Пусть M=[0,1] и A- нечеткое множество с элементами из универсального множестваEи множеством принадлежностейM.

Определение 7.3.Величинаназываетсявысотой нечеткого множества A.

Определение 7.4.Нечеткое множествоAнормально, если его высота равна 1, т.е. верхняя граница его функции принадлежности равна 1 ().

Определение 7.5.Принечеткое множество называетсясубнормальным.

Определение 7.6.Нечеткое множествопусто, если.

Непустое субнормальное множество 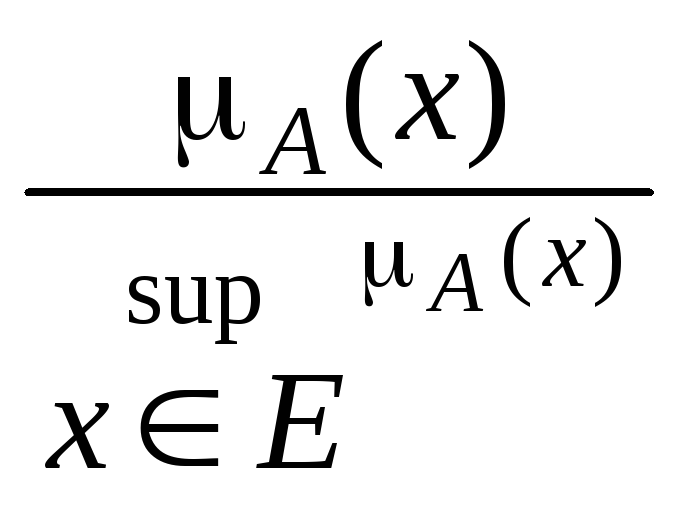можно нормализовать.

Определение 7.7.Нечеткое множество унимодально, µ_A(x)=1 только на одном x из E.

Носителем нечеткого множества A является обычное подмножество со свойством µ_A(x)>0, т.е. носитель A={x/µ_A(x)>0} ∀ x∈E.

Определение 7.8.Элементы xE, для которых µ_A(x)=0,5 называются точками перехода множества A.

Примеры нечетких множеств

Пример. Пусть E = {0,1,2,..,10}, M =[0,1]. Нечеткое множество "несколько" можно определить следующим образом: , его характеристики: высота = 1, носитель={3,4,5,6,7,8}, точки перехода - {3,8}.

Пример. Пусть E = {0,1,2,3,...,n,...}. Нечеткое множество "малый" можно определить:

“малый”=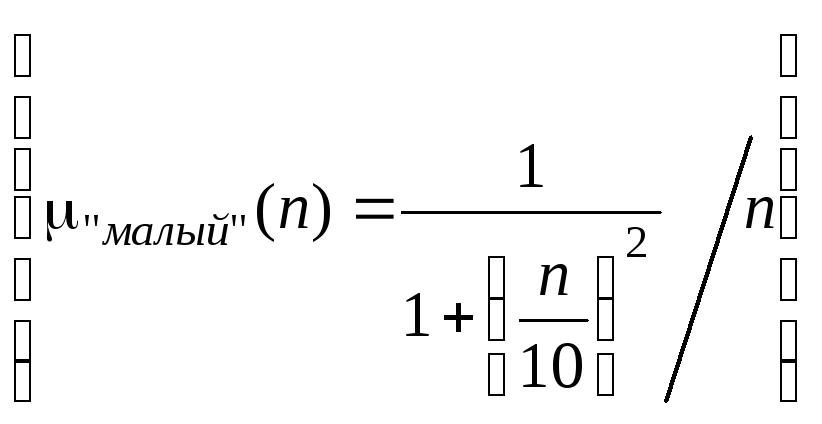

Пример. Пусть E = {1,2,3,...,100} и соответствует понятию "возраст", тогда нечеткое множество "молодой", может быть определено с помощью

µ_{"молодой"}(x)=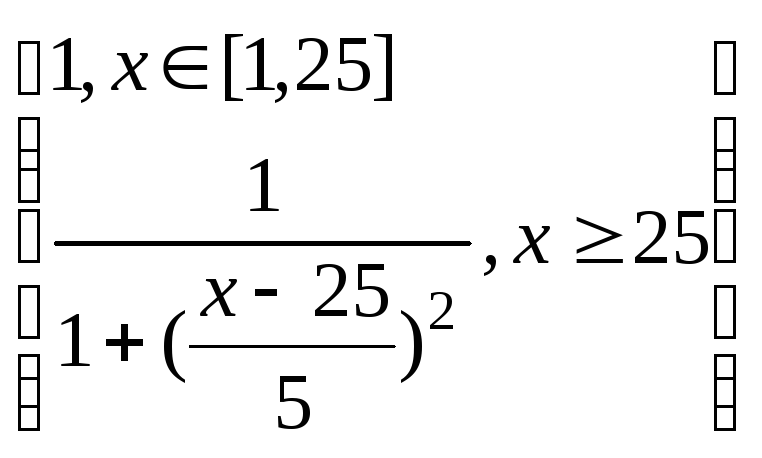

Нечеткое множество "молодой" на универсальном множестве E’={Иванов, Петров, Сидоров,...} задается с помощью функции принадлежности µ_{"молодой"}(x) на E={1,2,3,..100} (возраст), называемой по отношению к E’ функцией совместимости, при этом: , гдех – возраст Сидорова.

Операции над нечеткими множествами

Включение.

Пусть A и B - нечеткие множества на универсальном множестве E.

Говорят, что A содержится в B, если ∀x ∈E µ_A(x) µ_B(x).

Обозначение: A⊂B.

Иногда используют термин "доминирование", т.е. в случае когда A⊂B, говорят, что B доминирует A.

Равенство.

A и B равны, если ∀x∈E µ_A(x)=µ_B (x).

Обозначение: .

Дополнение.

Пусть Μ=[0,1], A и B - нечеткие множества, заданные на E. A и B дополняют друг друга, если ∀x∈E µ_A(x) = 1 - µ _B(x).

Обозначение: или.

Очевидно, что . (Дополнение определено дляM=[0,1], но очевидно, что его можно определить для любого упорядоченного M).

Пересечение.

AB - наибольшее нечеткое подмножество, содержащееся одновременно в A, и в B. .

Объединение.

АВ - наименьшее нечеткое подмножество, включающее как А, так и В, с функцией принадлежности: .

Разность.

с функцией принадлежности: .

Дизъюнктивная сумма.

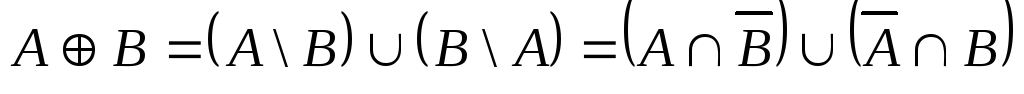с функцией принадлежности:

Примеры.

Пусть:

A = 0,4/ x₁ + 0,2/ x₂+0/ x₃+1/ x₄;

B = 0,7/ x₁+0,9/ x₂+0,1/ x₃+1/ x₄;

C = 0,1/ x₁+1/ x₂+0,2/ x₃+0,9/ x₄.

Здесь:

A⊂B, т.е. A содержится в B или B доминирует A, С несравнимо ни с A, ни с B, т.е. пары {A, С} и {A, С} - пары недоминируемых нечетких множеств.

A ≠ B ≠ C.

= 0,6/ x₁ + 0,8/x₂ + 1/x₃ + 0/x₄;

= 0,3/x₁ + 0,1/x₂ + 0,9/x₃ + 0/x₄.

A∩B = 0,4/x₁ + 0,2/x₂ + 0/x₃ + 1/x₄.

А∪В = 0,7/x₁ + 0,9/x₂ + 0,1/x₃ + 1/x₄. А - В = А∩ = 0,3/x1 + 0,1/x2 + 0/x3 + 0/x4;

В\А = ∩ В = 0,6/x1 + 0,8/x2 + 0,1/x3 + 0/x4.

А ⊕ В = 0,6/x1 + 0,8/x2 + 0,1/x3 + 0/x4.

Графическое представление операций

Для нечетких множеств можно строить визуальное представление. Рассмотрим прямоугольную систему координат, на оси ординат которой откладываются значения µ_A(x), на оси абсцисс в произвольном порядке расположены элементы E. Если E по своей природе упорядочено, то этот порядок желательно сохранить в расположении элементов на оси абсцисс. Такое представление делает наглядными простые операции над нечеткими множествами.

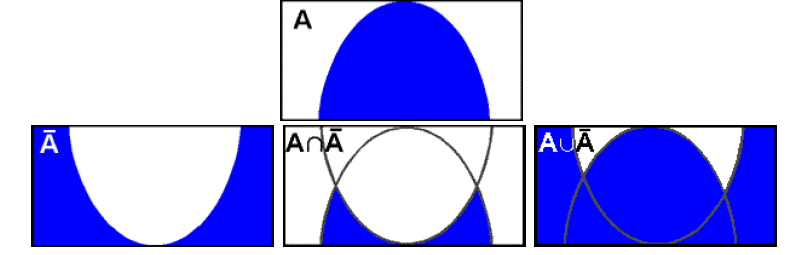На верхней части рисунка заштрихованная часть соответствует нечеткому множеству A и, если говорить точно, изображает область значений А и всех нечетких множеств, содержащихся в A. На нижней - даны , , .