Побудова дерева рішень за локальними показниками
|
|
Питома вага |
2005 |
2006 |
2007 |
2008 |
2009 |
|
Ф1 |
0,25 |
1,48 |
0,85 |
0,36 |
3,04 |
1,37 |
|
Ф2 |
0,2 |
0,89 |
1,37 |
0,53 |
0,4 |
0,11 |
|
Ф3 |
0,15 |
0,82 |
0,64 |
0,54 |
0,66 |
0,69 |
|
Ф4 |
0,15 |
0,25 |
0,16 |
0,05 |
0,13 |
0,16 |
|
Ф5 |
0,25 |
2,87 |
2,36 |
3,4 |
1,79 |
2,26 |
|
Кфін |
1 |
1,43 |
1,20 |
1,13 |
1,41 |
1,06 |
|
|
Питома вага |
2005 |
2006 |
2007 |
2008 |
2009 |
|
К1 |
0,25 |
1,17 |
0,88 |
0,95 |
1,28 |
1,19 |
|
К2 |
0,15 |
0,25 |
0,22 |
0,21 |
0,27 |
0,32 |
|
К3 |
0,15 |
0,07 |
0,05 |
0,01 |
0,04 |
0,05 |
|
К4 |
0,25 |
15,64 |
11,25 |
17,53 |
14,19 |
15,71 |
|
К5 |
0,2 |
0,09 |
0,49 |
0,09 |
0,29 |
0,08 |
|
Кклієнт |
1 |
4,27 |
3,17 |
4,67 |
3,97 |
4,30 |
|
|
Питома вага |
2005 |
2006 |
2007 |
2008 |
2009 |
|
П1 |
0,25 |
5,48 |
3,4 |
6,05 |
2,42 |
2,86 |
|
П2 |
0,3 |
2,48 |
1,94 |
3,06 |
1,85 |
2,15 |
|
П3 |
0,15 |
0,69 |
0,69 |
0,6 |
0,56 |
0,58 |
|
П4 |
0,2 |
1,13 |
0,95 |
0,98 |
1,08 |
1,36 |
|
П5 |
0,1 |
1,56 |
0,83 |
1,58 |
0,74 |
1,27 |
|
Кпер |
1 |
2,60 |
1,81 |
2,87 |
1,53 |
1,85 |
|
|
Питома вага |
2005 |
2006 |
2007 |
2008 |
2009 |
|
Б1 |
0,3 |
153,26 |
144,62 |
169,92 |
173,82 |
196,14 |
|
Б2 |
0,1 |
0,06 |
0,03 |
0,02 |
0,16 |
0,03 |
|
Б3 |
0,1 |
0,07 |
0,08 |
0,12 |
0,11 |
0,14 |
|
Б4 |
0,25 |
1,03 |
1 |
0,91 |
1 |
1,02 |
|
Б5 |
0,25 |
0,08 |
0,05 |
0,1 |
0,16 |
0,49 |
|
Кбізн |
1 |
46,27 |
43,66 |
51,24 |
52,46 |
59,24 |
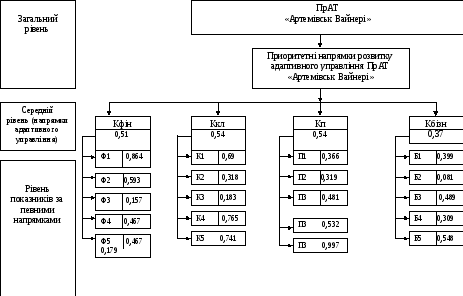
Рис.3.4 «Дерево рішень» для розробки стратегії розвитку
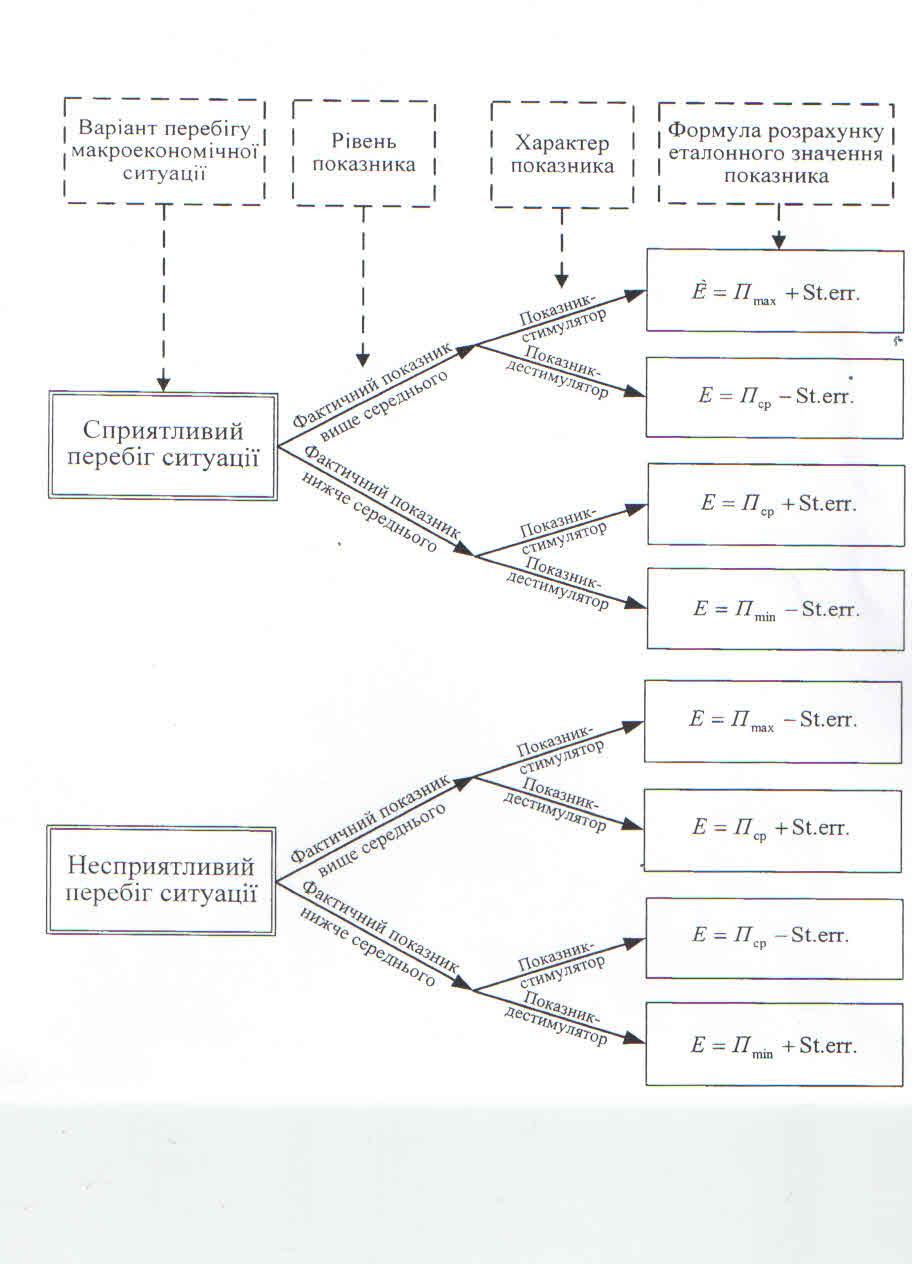
Рис. 3.5 Алгоритм вибору еталоних значень
Для подальшої побудови дерева рішень, обираємо в табл. 3.6 в значеннях локальних показників еталоні значення.
Таблиця 3.7
Розрахунок еталонів за оптимістичною та пісимістичню подією
|
|
Ф1 |
Ф2 |
Ф3 |
Ф4 |
Ф5 |
К1 |
К2 |
К3 |
К4 |
К5 |
П1 |
П2 |
П3 |
П4 |
П5 |
Б1 |
Б2 |
Б3 |
Б4 |
Б5 |
|
2005 |
1,48 |
0,89 |
0,82 |
0,25 |
2,87 |
1,17 |
0,25 |
0,07 |
15,6 |
0,09 |
5,48 |
2,48 |
0,69 |
1,13 |
1,56 |
153,26 |
0,06 |
0,07 |
1,03 |
0,08 |
|
2006 |
0,85 |
1,37 |
0,64 |
0,16 |
2,36 |
0,88 |
0,22 |
0,05 |
11,3 |
0,49 |
3,4 |
1,94 |
0,69 |
0,95 |
0,83 |
144,62 |
0,03 |
0,08 |
1 |
0,05 |
|
2007 |
0,36 |
0,53 |
0,54 |
0,05 |
3,4 |
0,95 |
0,21 |
0,01 |
17,5 |
0,09 |
6,05 |
3,06 |
0,6 |
0,98 |
1,58 |
169,92 |
0,02 |
0,12 |
0,91 |
0,1 |
|
2008 |
3,04 |
0,4 |
0,66 |
0,13 |
1,79 |
1,28 |
0,27 |
0,04 |
14,2 |
0,29 |
2,42 |
1,85 |
0,56 |
1,08 |
0,74 |
173,82 |
0,16 |
0,11 |
1 |
0,16 |
|
2009 |
1,37 |
0,11 |
0,69 |
0,16 |
2,26 |
1,19 |
0,32 |
0,05 |
15,7 |
0,08 |
2,86 |
2,15 |
0,58 |
1,36 |
1,27 |
196,14 |
0,03 |
0,14 |
1,02 |
0,49 |
|
|
Ф1 |
Ф2 |
Ф3 |
Ф4 |
Ф5 |
К1 |
К2 |
К3 |
К4 |
К5 |
П1 |
П2 |
П3 |
П4 |
П5 |
Б1 |
Б2 |
Б3 |
Б4 |
Б5 |
|
mean |
1,42 |
0,66 |
0,67 |
0,15 |
2,536 |
1,094 |
0,254 |
0,044 |
14,864 |
0,208 |
4,042 |
2,296 |
0,624 |
1,1 |
1,196 |
167,552 |
0,06 |
0,104 |
0,992 |
0,176 |
|
Minimum |
0,36 |
0,11 |
0,54 |
0,05 |
1,79 |
0,88 |
0,21 |
0,01 |
11,25 |
0,08 |
2,42 |
1,85 |
0,56 |
0,95 |
0,74 |
144,62 |
0,02 |
0,07 |
0,91 |
0,05 |
|
maximum |
3,04 |
1,37 |
0,82 |
0,25 |
3,4 |
1,28 |
0,32 |
0,07 |
17,53 |
0,49 |
6,05 |
3,06 |
0,69 |
1,36 |
1,58 |
196,14 |
0,16 |
0,14 |
1,03 |
0,49 |
|
Standart Error |
0,452 |
0,217 |
0,045 |
0,032 |
0,276 |
0,076 |
0,020 |
0,010 |
1,047 |
0,081 |
0,726 |
0,220 |
0,028 |
0,073 |
0,177 |
8,923 |
0,026 |
0,013 |
0,021 |
0,081 |
|
оптимістичне |
Ф1 |
Ф2 |
Ф3 |
Ф4 |
Ф5 |
К1 |
К2 |
К3 |
К4 |
К5 |
П1 |
П2 |
П3 |
П4 |
П5 |
Б1 |
Б2 |
Б3 |
Б4 |
Б5 |
|
среднее |
1,42 |
0,66 |
0,67 |
0,15 |
2,536 |
1,094 |
0,254 |
0,044 |
14,864 |
0,208 |
4,042 |
2,296 |
0,624 |
1,1 |
1,196 |
167,552 |
0,06 |
0,104 |
0,992 |
0,176 |
|
еталон |
1,872 |
-0,107 |
0,865 |
0,282 |
2,260 |
1,018 |
0,234 |
0,034 |
18,577 |
0,127 |
4,768 |
2,516 |
0,652 |
1,433 |
1,757 |
205,063 |
0,034 |
0,153 |
1,051 |
0,571 |
|
пісиместичне |
Ф1 |
Ф2 |
Ф3 |
Ф4 |
Ф5 |
К1 |
К2 |
К3 |
К4 |
К5 |
П1 |
П2 |
П3 |
П4 |
П5 |
Б1 |
Б2 |
Б3 |
Б4 |
Б5 |
|
среднее |
1,42 |
0,66 |
0,67 |
0,15 |
2,536 |
1,094 |
0,254 |
0,044 |
14,864 |
0,208 |
4,042 |
2,296 |
0,624 |
1,1 |
1,196 |
167,552 |
0,06 |
0,104 |
0,992 |
0,176 |
|
еталон |
0,968 |
0,443 |
0,775 |
0,218 |
2,260 |
1,170 |
0,274 |
0,054 |
16,483 |
0,289 |
3,316 |
2,076 |
0,596 |
1,287 |
1,403 |
187,217 |
0,034 |
0,127 |
1,009 |
0,409 |
Якщо показник дестимулятор: середнє = Mean - Standard Error; якщо фактичне значення величини показника останнього року вище середнього за досліджуваний період, змодельоване еталонне розраховується: Mean - Standard Error; якщо фактичне значення нижче середнього за досліджуваний період, змодельована величина = Minimum - Standard Error;
При песимістичному сценарії розвитку якщо показник стимулятор: середнє = Mean - Standard Error; змодельоване еталонне: якщо фактичне значення величини показника за останній рік досліджуваного періоду вище середнього за весь період = Maximum - Standard Error; якщо фактичне значення нижче середнього = Mean - Standard Error.
Якщо показник дестимулятор: середнє = Mean + Standard Error; змодельоване еталонне: якщо фактичне значення показника за останній рік досліджуваного періоду вище середнього = Mean + Standard Error; якщо фактичне значення показника за останній рік досліджуваного періоду нижче середнього, змодельоване еталонне = Minimum + Standard Error.
Аналіз паралельних рядів імітаційного розподілу за допомогою формули Фехнера дозволив виявити існування найбільш типових комбінацій розподілу напрямків соціального розвитку, що можуть бути використані в разі проведення аналогічних досліджень в майбутньому
У даному функціональному блоці алгоритму відбору напрямку соціального розвитку відповідно до методу Монте-Карло за допомогою пакета аналізу даних Microsoft Ехсеl проводилося моделювання величини показника соціального розвитку в залежності від зміни окремих факторів, що його формують з метою визначення його максимальних значень як при оптимістичному, так і при песимістичному сценарії й вибору пріоритетних напрямків інвестування (таблиці 3.8, 3.9).
|
|
Ф1 |
Ф2 |
Ф3 |
Ф4 |
Ф5 |
Кфін |
К1 |
К2 |
К3 |
К4 |
К5 |
Ккл |
П1 |
П2 |
П3 |
П4 |
П5 |
Кп |
Б1 |
Б2 |
Б3 |
Б4 |
Б5 |
Кбізн |
|
питома вага |
0,25 |
0,20 |
0,15 |
0,15 |
0,25 |
1 |
0,25 |
0,15 |
0,15 |
0,25 |
0,20 |
1 |
0,25 |
0,30 |
0,15 |
0,20 |
0,10 |
1 |
0,30 |
0,10 |
0,10 |
0,25 |
0,25 |
1 |
|
2005 |
1,48 |
0,89 |
0,82 |
0,25 |
2,87 |
1,43 |
1,17 |
0,25 |
0,07 |
15,64 |
0,09 |
4,27 |
5,48 |
2,48 |
0,69 |
1,13 |
1,56 |
2,60 |
153,26 |
0,06 |
0,07 |
1,03 |
0,08 |
46,27 |
|
2006 |
0,85 |
1,37 |
0,64 |
0,16 |
2,36 |
1,20 |
0,88 |
0,22 |
0,05 |
11,25 |
0,49 |
3,17 |
3,40 |
1,94 |
0,69 |
0,95 |
0,83 |
1,81 |
144,62 |
0,03 |
0,08 |
1,00 |
0,05 |
43,66 |
|
2007 |
0,36 |
0,53 |
0,54 |
0,05 |
3,40 |
1,13 |
0,95 |
0,21 |
0,01 |
17,53 |
0,09 |
4,67 |
6,05 |
3,06 |
0,60 |
0,98 |
1,58 |
2,87 |
169,92 |
0,02 |
0,12 |
0,91 |
0,10 |
51,24 |
|
2008 |
3,04 |
0,40 |
0,66 |
0,13 |
1,79 |
1,41 |
1,28 |
0,27 |
0,04 |
14,19 |
0,29 |
3,97 |
2,42 |
1,85 |
0,56 |
1,08 |
0,74 |
1,53 |
173,82 |
0,16 |
0,11 |
1,00 |
0,16 |
52,46 |
|
2009 |
1,37 |
0,11 |
0,69 |
0,16 |
2,26 |
1,06 |
1,19 |
0,32 |
0,05 |
15,71 |
0,08 |
4,30 |
2,86 |
2,15 |
0,58 |
1,36 |
1,27 |
1,85 |
196,14 |
0,03 |
0,14 |
1,02 |
0,49 |
59,24 |
|
1 |
1,87 |
0,11 |
0,69 |
0,16 |
2,26 |
1,18 |
1,19 |
0,32 |
0,05 |
15,71 |
0,08 |
4,30 |
2,86 |
2,15 |
0,58 |
1,36 |
1,27 |
1,85 |
196,14 |
0,03 |
0,14 |
1,02 |
0,49 |
59,24 |
|
2 |
1,37 |
-0,11 |
0,69 |
0,16 |
2,26 |
1,01 |
1,19 |
0,32 |
0,05 |
15,71 |
0,08 |
4,30 |
2,86 |
2,15 |
0,58 |
1,36 |
1,27 |
1,85 |
196,14 |
0,03 |
0,14 |
1,02 |
0,49 |
59,24 |
|
3 |
1,37 |
0,11 |
0,87 |
0,16 |
2,26 |
1,08 |
1,19 |
0,32 |
0,05 |
15,71 |
0,08 |
4,30 |
2,86 |
2,15 |
0,58 |
1,36 |
1,27 |
1,85 |
196,14 |
0,03 |
0,14 |
1,02 |
0,49 |
59,24 |
|
4 |
1,37 |
0,11 |
0,69 |
0,28 |
2,26 |
1,08 |
1,19 |
0,32 |
0,05 |
15,71 |
0,08 |
4,30 |
2,86 |
2,15 |
0,58 |
1,36 |
1,27 |
1,85 |
196,14 |
0,03 |
0,14 |
1,02 |
0,49 |
59,24 |
|
5 |
1,37 |
0,11 |
0,69 |
0,16 |
2,26 |
1,06 |
1,19 |
0,32 |
0,05 |
15,71 |
0,08 |
4,30 |
2,86 |
2,15 |
0,58 |
1,36 |
1,27 |
1,85 |
196,14 |
0,03 |
0,14 |
1,02 |
0,49 |
59,24 |
|
6 |
1,37 |
0,11 |
0,69 |
0,16 |
2,26 |
1,06 |
1,02 |
0,32 |
0,05 |
15,71 |
0,08 |
4,25 |
2,86 |
2,15 |
0,58 |
1,36 |
1,27 |
1,85 |
196,14 |
0,03 |
0,14 |
1,02 |
0,49 |
59,24 |
|
7 |
1,37 |
0,11 |
0,69 |
0,16 |
2,26 |
1,06 |
1,19 |
0,23 |
0,05 |
15,71 |
0,08 |
4,28 |
2,86 |
2,15 |
0,58 |
1,36 |
1,27 |
1,85 |
196,14 |
0,03 |
0,14 |
1,02 |
0,49 |
59,24 |
|
8 |
1,37 |
0,11 |
0,69 |
0,16 |
2,26 |
1,06 |
1,19 |
0,32 |
0,03 |
15,71 |
0,08 |
4,29 |
2,86 |
2,15 |
0,58 |
1,36 |
1,27 |
1,85 |
196,14 |
0,03 |
0,14 |
1,02 |
0,49 |
59,24 |
|
9 |
1,37 |
0,11 |
0,69 |
0,16 |
2,26 |
1,06 |
1,19 |
0,32 |
0,05 |
18,58 |
0,08 |
5,01 |
2,86 |
2,15 |
0,58 |
1,36 |
1,27 |
1,85 |
196,14 |
0,03 |
0,14 |
1,02 |
0,49 |
59,24 |
|
10 |
1,37 |
0,11 |
0,69 |
0,16 |
2,26 |
1,06 |
1,19 |
0,32 |
0,05 |
15,71 |
0,13 |
4,31 |
2,86 |
2,15 |
0,58 |
1,36 |
1,27 |
1,85 |
196,14 |
0,03 |
0,14 |
1,02 |
0,49 |
59,24 |
|
11 |
1,37 |
0,11 |
0,69 |
0,16 |
2,26 |
1,06 |
1,19 |
0,32 |
0,05 |
15,71 |
0,08 |
4,30 |
4,77 |
2,15 |
0,58 |
1,36 |
1,27 |
2,32 |
196,14 |
0,03 |
0,14 |
1,02 |
0,49 |
59,24 |
|
12 |
1,37 |
0,11 |
0,69 |
0,16 |
2,26 |
1,06 |
1,19 |
0,32 |
0,05 |
15,71 |
0,08 |
4,30 |
2,86 |
2,52 |
0,58 |
1,36 |
1,27 |
1,96 |
196,14 |
0,03 |
0,14 |
1,02 |
0,49 |
59,24 |
|
13 |
1,37 |
0,11 |
0,69 |
0,16 |
2,26 |
1,06 |
1,19 |
0,32 |
0,05 |
15,71 |
0,08 |
4,30 |
2,86 |
2,15 |
0,65 |
1,36 |
1,27 |
1,86 |
196,14 |
0,03 |
0,14 |
1,02 |
0,49 |
59,24 |
|
14 |
1,37 |
0,11 |
0,69 |
0,16 |
2,26 |
1,06 |
1,19 |
0,32 |
0,05 |
15,71 |
0,08 |
4,30 |
2,86 |
2,15 |
0,58 |
1,43 |
1,27 |
1,86 |
196,14 |
0,03 |
0,14 |
1,02 |
0,49 |
59,24 |
|
15 |
1,37 |
0,11 |
0,69 |
0,16 |
2,26 |
1,06 |
1,19 |
0,32 |
0,05 |
15,71 |
0,08 |
4,30 |
2,86 |
2,15 |
0,58 |
1,36 |
1,76 |
1,89 |
196,14 |
0,03 |
0,14 |
1,02 |
0,49 |
59,24 |
|
16 |
1,37 |
0,11 |
0,69 |
0,16 |
2,26 |
1,06 |
1,19 |
0,32 |
0,05 |
15,71 |
0,08 |
4,30 |
2,86 |
2,15 |
0,58 |
1,36 |
1,27 |
1,85 |
205,06 |
0,03 |
0,14 |
1,02 |
0,49 |
61,91 |
|
17 |
1,37 |
0,11 |
0,69 |
0,16 |
2,26 |
1,06 |
1,19 |
0,32 |
0,05 |
15,71 |
0,08 |
4,30 |
2,86 |
2,15 |
0,58 |
1,36 |
1,27 |
1,85 |
196,14 |
0,03 |
0,14 |
1,02 |
0,49 |
59,24 |
|
18 |
1,37 |
0,11 |
0,69 |
0,16 |
2,26 |
1,06 |
1,19 |
0,32 |
0,05 |
15,71 |
0,08 |
4,30 |
2,86 |
2,15 |
0,58 |
1,36 |
1,27 |
1,85 |
196,14 |
0,03 |
0,15 |
1,02 |
0,49 |
59,24 |
|
19 |
1,37 |
0,11 |
0,69 |
0,16 |
2,26 |
1,06 |
1,19 |
0,32 |
0,05 |
15,71 |
0,08 |
4,30 |
2,86 |
2,15 |
0,58 |
1,36 |
1,27 |
1,85 |
196,14 |
0,03 |
0,14 |
1,05 |
0,49 |
59,24 |
|
20 |
1,37 |
0,11 |
0,69 |
0,16 |
2,26 |
1,06 |
1,19 |
0,32 |
0,05 |
15,71 |
0,08 |
4,30 |
2,86 |
2,15 |
0,58 |
1,36 |
1,27 |
1,85 |
196,14 |
0,03 |
0,14 |
1,02 |
0,57 |
59,26 |
Таблиця 3.8