Частина 2. Побудова стохастичних моделей систем

Стохастичні моделі – це моделі систем, в яких суттєву роль відіграє випадок. Зв’язок між вхідними й вихідними величинами стохастичних систем має випадковий характер.

Явища в природі бувають детерміновані й випадкові. Вивчаючи електромеханічні системи, ми маємо справу в основному з детермінованими процесами, тобто процесами і явищами, які можна розрахувати на основі відомих співвідношень. Вся інженерна освіта направлена в першу чергу на вивчення детермінованих явищ, їх закономірностей. Проте поряд з такими явищами існують інші явища, які мають випадковий характер і розрахувати їх протікання, конкретні значення величин неможливо. Можна тільки передбачити імовірність певного стану. Процеси виробництва та експлуатації електромеханічних систем пов’язані з впливом великого ряду зовнішніх дій, результати яких проявляються як випадкові величини. Причини випадковості довгий час пояснювали виходячи з недостатньої інформації і вважали, що коли буде достатньо інформації, то все можна передбачити, розрахувати і жодного випадкового явища не буде. Але це не так. Хоча все в природі має свої причини, діє причинно-наслідкова залежність, проте є цілий ряд явищ, які мають чисто випадковий характер. Природі притаманна випадковість, вона лежить в основі явищ навколишнього світу. Випадковість не означає повного безладу, неможливості передбачити, як поведе себе система в тих чи інших умовах. Випадкові події підлягають певним закономірностям, завдяки яким можна підрахувати ймовірність тій чи іншої події, оцінити, які результати можливі при тій чи іншій дії та оцінити ймовірність кожного результату.

Існують дві наукові дисципліни (два розділи математики), які вивчають властивості випадкових величин [11-15]. Вони є основою побудови стохастичних моделей і розгляду випадкових явищ в стохастичних моделях. Це теорія ймовірності та математична статистика.

Теорія ймовірностей – це наукова дисципліна, яка вивчає випадкові події та процеси, розробляє методи обчислення ймовірностей одних випадкових подій за ймовірностями інших.

Математична статистика – це наукова дисципліна, яка вивчає математичні методи систематизації та використання статистичних даних, вирішення наукових і практичних завдань на базі обмежених статистичних даних. Вона вивчає закономірності масових явищ та їх взаємозв’язки. Математична статистика ґрунтується на теорії ймовірностей, яка дозволяє обрахувати точність та надійність статистичних висновків.

Стохастичні моделі – це моделі, побудовані з урахуванням ймовірностей різних подій, засновані на використанні законів ймовірностей та математичної статистики. У діяльності інженера-електромеханіка ці моделі мають навіть більше практичне значенні ніж детерміновані моделі, оскільки в процесі виробництво, обслуговування та експлуатація електромеханічних систем, засобів електротранспорту, завжди доводиться мати справу з випадковими величинами, з впливом факторів, які мають масовий характер. Для вивчення особливостей стохастичних моделей рекомендується використати літературу [12-15].

Задача 3. Відшукання залежності між температурою перегріву трансформатора і струмом холостого ходу. Кореляція та лінійна регресія

Відповідно до варіанта роботи створити масив даних для вирішення задачі аналізу. Побудувати гістограми розподілу випадкових величини: струму холостого ходу трансформатора та температури перегріву трансформатора. Перевірити лінійну кореляційну залежність між цими величинами. В разі наявності кореляційної залежності побудувати рівняння лінійної регресії. Оцінити ступінь залежності між величиною струму та температурою перегріву і зробити рекомендації щодо використанню цієї залежності для оцінки якості трансформаторів у процесі їх виготовлення.

У даному завданні РГР потрібно:

1. Ввести назву другої частини розрахунково-графічної роботи та пояснювальний текст до розрахунково-графічної роботи.

2. Сформувати, відповідно до варіанта завдання, масиви вихідних даних для виконання роботи

3. Виконати аналіз вихідних даних. Побудувати гістограму розподілу випадкових величин струму холостого ходу та температури перегріву трансформатора.

4. Побудувати еліпс розсіяння струму холостого ходу Іхх і температури нагріву t трансформатора.

5. Виконати кореляційний аналіз.

6. Виконати регресійний аналіз, вивівши графік нормальної імовірності та графік остатків.

7. Виконати аналіз результатів розрахунку.

8. Записати рівняння лінійної регресії і оцінити ступінь достовірності їх значень, вивести рівняння регресії на графіку еліпса розсіяння.

9. Виконати аналіз щодо доцільності використання одержаних залежностей для оцінки якості трансформаторів на виробництві.

10. Зробити висновки й оформити звіт.

Зміст роботи:

Важливими характеристиками трансформаторів різного типу є величина струму холостого ходу й температура перегріву обмотки в робочому та аномальних режимах роботи. Ці характеристики визначають якість трансформатора, його придатність до експлуатації. Однозначної залежності між ними не існує. Струм холостого ходу визначається матеріалом магнітопроводу, величиною немагнітних зазорів, потоків розсіяння та ін. Перегрів обмотки залежить від втрат в обмотці та магнітопроводі й характеристик відводу тепла від трансформатора. Проте для деяких типів трансформаторів, наприклад виготовлених на витому магнітопроводі, існує ряд причин, що приводять до одночасного збільшення струму холостого ходу і температури перегріву. Однією з таких причин є зменшення електричного опору між пластинами сталі в місці розрізу магнітопроводу. Встановлення статистичної залежності між струмом холостого ходу і температурою перегріву має практичне значення і може бути використане процесі виробництва трансформаторів. Наприклад, сортувати трансформатори за величиною допустимого перегріву, при наявності статистичної взаємозалежності, можна виміривши струм холостого ходу, що значно простіше.

Кореляційною залежністю величин називають функціональну залежність умовного (чи групового) середнього або зворотну їй функцію. При цьому одержане рівняння називають рівнянням регресії [12].

Якщо побудувати так зване кореляційне поле, відкладаючи по осях значення величин Х та Y, то видно його деяку розмитість. Якщо число величин велике, то кореляційне поле має вигляд більш-менш правильного еліпса, в якого точки трохи згущені в центрі і відносно мало розміщені на периферії. Таке кореляційне поле називають еліпсом розсіяння. Якщо кореляційне поле витягується уздовж діагоналі, то це є свідченням наявності кореляції між величинами. Йому у відповідність можна поставити певну функцію, яка зв’язує ознаки Х та У. Якщо еліпс розсіяння витягується паралельно до однієї з осей діаграми, то це свідчить тільки про зміну масштабу даних, а не про їх взаємозв’язок [13,14].

Важливо відзначити, що встановлення кореляції між ознаками і одержане рівняння регресії не дає підстав вважати, що зв’язок між величинами чи ознаками є зв’язком причинно-наслідковим. Можливо, що ці ознаки залежать від якихось інших ознак.

Відхилення осі еліпса розсіяння від напрямку координатних осей свідчить, що середнє значення однієї ознаки залежить від значення іншої. Такий випадок називають лінійною регресією. Зрозуміло, що точки ніколи не розміщуються по одній прямій і завданням аналізу є знайти рівняння такої лінії, яка б проходила найбільш близько до всіх точок. Таку лінію відшукують методом найменших квадратів. При двох ознаках можна побудувати два рівняння (дві лінії) регресії, а саме від Х тавідY. Вони завжди різні, за винятком є однозначної лінійна залежності між величинами Х та Y. Для практичних цілей можуть розглядуватись обидва рівняння регресії. При розмитості кореляції коефіцієнти рівнянь регресії різні. У більшості випадків розглядають тільки одне з рівнянь, залежно від того, яка з величин вибрана більш важливою і вважається залежною. Важливим завданням теорії кореляції є знаходження числового параметра, який дає кількісну оцінку ступеня залежності між випадковими величинами. Таким параметром є коефіцієнт кореляції R. Він може приймати значення від 1 до 0. Кореляція вважається тим сильнішою, чим тісніше точки кореляційного поля групуються коло лінії регресії. Якщо кореляція повна (немає неврахованих впливів), то точки розміщуються на одній прямій, обидва рівняння регресії співпадають, вони відповідають лінійній залежності між величинами і коефіцієнт кореляції дорівнює r=1, тобто існує повна функціональна лінійна залежність величин.

Якщо дві величини є випадкові й незалежні, то кореляція між ними відсутня і коефіцієнт кореляції дорівнює нулю r=0.

Для характеристики наявності кореляційного зв’язку вводять поняття суттєвості зв’язку. Кореляційний зв’язок можна вважати суттєвим, якщо коефіцієнт кореляції значимо відрізняється від нуля. З метою перевірити значимість коефіцієнта кореляції використовують таблиці розподілу складені для величини критерію z [12-14]. Тут використовують методи перевірки статистичних гіпотез, а саме гіпотези H₀:, що коефіцієнт кореляції має нульове значення, H₀: r =0. Для перевірки нульової гіпотези розраховують статистику z:

(46)

Якщо розрахована величина більша від критичного значення, для заданого рівня значимості альфа, при числі ступенів свободи f=N-2, де N – число точок, то коефіцієнт кореляції вважають суттєво відмінним від нуля.

Іншою ознакою відмінності коефіцієнта кореляції від 0 може служити F – критерій Фішера, який розраховують методами дисперсійного аналізу, відповідні теоретичні відомості можна знайти в [12].

Для випадку, коли коефіцієнт кореляції суттєво відмінний від нуля, величина R² може розглядатись, як оцінка ступеня впливу незалежної величини на величину, яка прийнята залежною. Кількісною оцінкою впливу можна вважати величину R² виражену в процентах.

Лінійну регресію, як правило, показують у вигляді графіка.

Порядок виконання роботи:

1. Ввести назву другої частини розрахунково-графічної роботи та пояснювальний текст до розрахунково-графічної роботи, як вказано в лабораторній роботі №9 [1].

2. Сформувати масив вихідних даних для виконання роботи відповідно до варіанта завдання.

Робота виконується для масиву даних, які студент генерує самостійно. Для виконання роботи потрібно самостійно згенерувати 50 значень струму холостого ходу трансформатора Іхх в (мА), та відповідних їм значень температури перегріву обмотки трансформатора (t, C). Порядок генерування вихідних даних описано в п. 4.4 – 4.16 лабораторної роботи № 9 [1]. Слід звернути увагу на те, що дані струму холостого ходу трансформатора Іхх генеруються, як величини розподілені за рівномірним законом, а дані температури перегріву обмотки t – розподілені відповідно до нормального законом розподілу випадкових величин. Причому генерація значень температури здійснюється у декілька етапів в двох колонках електронної таблиці, а після цього дані переносяться в одну колонку t і всі допоміжні розрахунки вилучають.

3. Виконання аналізу вихідних даних та побудову гістограм розподілу здійснюютьяк вказано у п. 4.17 – 4.28 лабораторної роботи № 9 [1]. Слід зауважити, що після побудови гістограм їх розміри потрібно збільшити і перемістити на екрані так, щоб гістограми було зручно аналізувати й роздрукувати.

4. Побудову еліпсу розсіяння струму холостого ходу Іхх і температури нагріву t трансформатора виконують в порядку, вказаному в п. 4.29 – 4.31 лабораторної роботи № 9 [1] як точкова діаграма.

5. Кореляційний аналіз залежності струму холостого ходу Іхх і температури нагріву t трансформатора слід виконати в такому порядку:

Викликати програму кореляційного аналізу, яка входить в пакет „АНАЛИЗ ДАННЫХ” (рис.2) за допомогою команди: „СЕРВИС > АНАЛИЗ ДАННЫХ > КОРРЕЛЯЦИЯ”.

Рис. 2 – Вікно меню пакету „АНАЛИЗ ДАННЫХ”

У вікні кореляційного аналізу (див.рис.3) вказати вхідний інтервал даних, виділивши всі дані, в якості вихідного інтервалу вказують вільне місце на цій же сторінці.

Рис. 3 – Діалогове вікно кореляційного аналізу пакету „АНАЛИЗ ДАННЫХ”

Подати команду на виконання аналізу й після її виконання проаналізувати результати аналізу, враховуючи значення коефіцієнта кореляції. Коефіцієнт кореляції – це недіагональний елемент кореляційної таблиці, як показано на рис. 4:

	Іхх	Δt
Іхх	1
Δt	-0,11	1

Рис. 4 – Кореляційна таблиця

6. Виконання регресійного аналізу та вивід графіка нормального розподілу і графіка остатків.

Порядок виконання регресійного аналізу наведено в п. 4.32 – 4.39 лабораторної роботи № 9 [1]. У вікні регресія (див.рис.5) слід вказати:

• вхідний інтервал у для залежної змінної, виділивши значення разом з позначенням t;

• вхідний інтервал х для залежної змінної Іхх;

• поставити позначку «Метки», якщо в діапазон значень ввійшли клітини з позначенням величин;

• ввести значення рівня надійності 99%;

• поставити позначку у вікнах: «График остатков», «График подбора» та «График нормальной вероятности»;

• як вихідний інтервал вказати клітинку, починаючи з якої бажано вивести графік на цій же робочій сторінці.

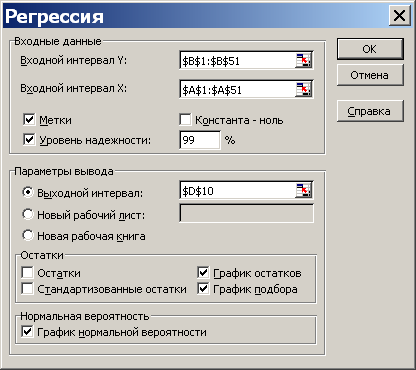
Рис. 5 – Вікно регресійного аналізу пакету „АНАЛИЗ ДАННЫХ”

Результати аналізу виводя у вигляді таблиць та графіків.

Першою є таблиця регресійної статистики (рис.6). У ній наведені значення коефіцієнта регресії R, значення R² і величина стандартної похибки (середньоквадратичне відхилення результатів вимірювання температури перегріву)

Регрессионная статистика
Множественный R	0,941
R-квадрат	0,886
Нормированный R-квадрат	0,884
Стандартная ошибка	1,535
Наблюдения	50

Рис. 6 – Приклад таблиці регресійної статистики

Другою – таблиця дисперсійного аналізу (рис.7). Вона дозволяє зробити висновок про суттєвість впливу величини прийнятої незалежною х, (струму холостого ходу) на залежну величину у (температуру перегріву). Висновок робиться на основі порівняння величини критерію Фішера «F», розрахованого за вихідними даними, з критичним значенням величини, яке знаходиться згідно з математичними таблицями. У таблиці дисперсійного аналізу в колонці «Значимость F» подано величину значущості коефіцієнта регресії. Якщо розрахована за статистичними даними величина значимості не перевищує 0,05 (0,01 у випадку коли вибраний рівень надійності 99% (див.рис.4)), то слід зробити висновок про суттєвість впливу і відмінність коефіцієнта регресії від нуля. Оцінкою ступеня впливу є значення R², подане в таблиці регресійної статистики.

	df	SS	MS	F	Значимость F
Регрессия	1	883,99	883,99	374,78	2,55E-24
Остаток	48	113,21	2,3586
Итого	49	997,20

Рис. 7 – Приклад таблиці дисперсійного аналізу

Третя – таблиця регресійного аналізу (див.рис.8). У ній виведені розраховані значення коефіцієнтів регресії, стандартна похибка, значення статистики Стьюдента (t-статистика), імовірності (P) та значення довірчого інтервалу при 95% довірчій імовірності й вибраній нами 99% довірчій імовірності.

	Коэффи- циенты	Стан-дартная ошибка	t- статис- тика	P-Значе- ние	Ниж- ние 95%	Верх- ние 95%	Ниж- ние 99,0%	Верх- ние 99,0%
Y-пересе- чение	28,83	0,845	3,409	0,001	1,18	4,58	0,61	5,15
Іхх	0,292	0,015	19,359	10-24	0,26	0,32	0,25	0,33

Рис. 8 – Приклад таблиці регресійного аналізу

За даними розрахунків побудовані й виводяться графіки для кожної пари змінних. У нашому випадку виведено три графіки, а саме: графік нормального розподілу, графік залишків та графік підбору.

На основі графіка нормального розподілу робиться висновок, в якій мірі розподіл температури перегріву трансформаторів підлягає нормальному закону розподілу ймовірностей. Якщо графік можна описати прямою лінією, то розподіл близький до нормального закону. Справа в тому, що статистичні виводи для вирішення багатьох практичних завдань засновані на допущенні, що випадкові величини підлягають нормальному закону розподілу ймовірностей. Тому під час вирішення практичних завдань виникає необхідність оцінки, чи розподіл величин може вважатись нормальним.

Графік залишків показує еліпс розсіяння залишків після вилучення функціональної залежності, яка описується рівнянням регресії. За значеннями еліпса розсіяння залишків можна судити, в якій мірі вилучення функціональної залежності зменшує величину відхилення досліджуваних величин, викликану випадковими факторами. Еліпс розсіяння остатків повинен мати вісь, розміщену вздовж однієї з координатних осей, а при зміні масштабу перетворюватись в коло.

Графік підбору показує розміщення лінії регресії на графіку кореляційного поля.

7. Виконання аналізу результатів розрахунку здійснюють відповідно до завдань роботи з урахуванням рекомендацій, які наведені вище.

8. Рівняння лінійної регресії записують у вигляді t = 0,292*Іхх + 28,83, де коефіцієнтами є результати розрахунків коефіцієнтів регресії, подані в таблиці регресійного аналізу. Ступінь достовірності значень коефіцієнтів регресії оцінюється за величиною критерію Стьюдента згідно з t-статистиці, та значення імовірності (P). Рівняння регресії вивести на графік можна, скориставшись правою клавішею маніпулятора «мишка», вибравши з контекстного меню «ЛИНИЯ ТРЕНДА» і вказавши як параметр: «ПОКАЗЫВАТЬ УРАВНЕНИЕ».

9. Аналіз щодо доцільності використання одержаних залежностей для оцінки якості трансформаторів на виробництві виконують відповідно до значення величини коефіцієнта R². У прикладі, розглянутому на рис. 5, значення R² = 0,88. Це свідчить, що майже 88% зміни температури нагріву обумовлено величиною струму холостого ходу.

10. Звіт з виконаного завдання оформляють відповідно до правил оформлення звітів і роздруковують на окремих аркушах паперу.

Завдання 4. Аналіз пробігу шин коліс тролейбуса. Двофакторний дисперсійний аналіз

У тролейбусне депо потрібно закупити певну кількість покришок для коліс тролейбусів. Покришки випускають три заводи: №1, №2 і №3. Вартість покришок цих заводів однакова. З досвіду роботи відомо, що якість покришок різних заводів різна. Крім цього практика експлуатації показала, що покришки по різному ведуть себе на різних маршрутах, які відрізняються типом дороги і дорожнього покриття. У депо є досвід використання покришок цих заводів протягом певного часу і зібрані статистичні дані. Використовуючи ці дані, інженеру потрібно зробити заявку на закупівлю покришок. У заявці вказати скільки покришок якого заводу треба закупити з урахуванням того, щоб їх експлуатація була якомога ефективнішою. У пояснювальній записці на ім’я директора депо треба обґрунтувати подану заявку, навівши результати виконаного аналізу.

У даному завданні РГР потрібно:

1. Створити масив даних відповідно до варіанта роботи.

2. Виконати за допомогою пакету „АНАЛИЗ ДАННЫХ” двофакторний дисперсійний аналіз.

3. Виконати математичний аналіз результатів і записати математичну модель.

4. Виконати інтерпретацію результатів з поясненнями.

5. Оформити заявку на закупку шин для депо, відповідно до потреб вказаних у табл. 4.

6. Оформити пояснювальну записку з обґрунтуванням заявки на закупку.