3.4 Взаимное пересечение плоскостей общего положения

Рассмотрим пример, в котором плоскости заданы треугольником и параллелограммом (Рис. 3.5). Требуется построить линию пересечения этих фигур. Для построения искомой линии достаточно найти две точки, в которых стороны одной фигуры пересекают плоскость другой фигуры. Поэтому возьмем одну из сторон параллелограмма, например, EF, и найдем точку пересечения ее с плоскостью треугольника. Для построения точки I, в которой прямая EF пересекает плоскость треугольника, проведем через EF горизонтально-проецирующую плоскость Р (след Р_н), находим проекции 1_н, 2_н и 1_v, 2_v линии пересечения проведенной вспомогательной плоскости Р с треугольником. В пересечении прямых 1_v 2_v и E_vF_v находим I_v и затем I_н, т.е. искомую точку. Таким же образом, посредством вспомогательной плоскости R, найдена точка II, в которой сторона параллелограмма DK пересекается с плоскостью треугольника. Остается соединить одноименные проекции найденных точек I и II.

Рис. 3.5. Взаимное пересечение плоскостей

Видимость плоских фигур определяется с помощью конкурирующих точек.

При помощи плоскостей – посредников можно найти общие точки, принадлежащие двум пересекающимся плоскостям, не имеющих общих точек на чертеже (Рис.3.6).

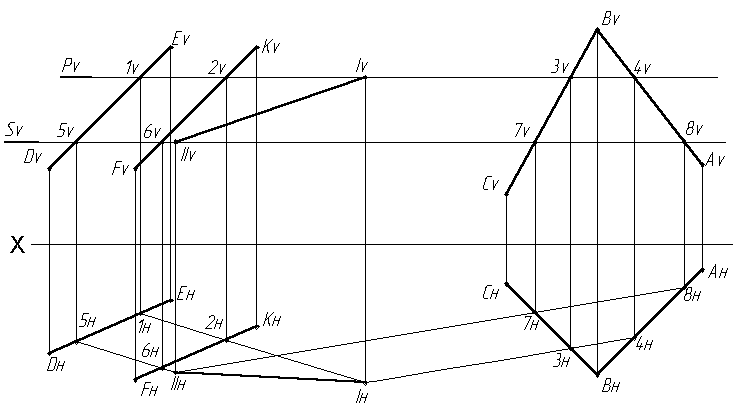
Рис 3.6. Построение линии пересечения двух плоскостей, не имеющих общих точек

Вводим горизонтальную плоскость – посредник Р (след P_v). Эта плоскость пересекает заданные плоскости по линиям уровня (горизонталям 1-2 и 3-4), в пересечении которых и лежит общая для всех трех плоскостей искомая точка I (проекции I_v и I_н). Для определения второй общей точки (II) проводится вспомогательная плоскость S.

3.5. Прямая, параллельная плоскости

Прямая параллельна плоскости, если она параллельна прямой, лежащей в плоскости.

Задача: Через точку А провести одну из возможных прямых, параллельных заданной плоскости (Рис.3.7).

Решение.

Чтобы построить прямую, параллельную заданной плоскости, следует взять в плоскости какую-либо прямую (например, D1) и параллельно ей через точку А провести искомую прямую. Можно также провести прямую, параллельную одной из сторон треугольника.

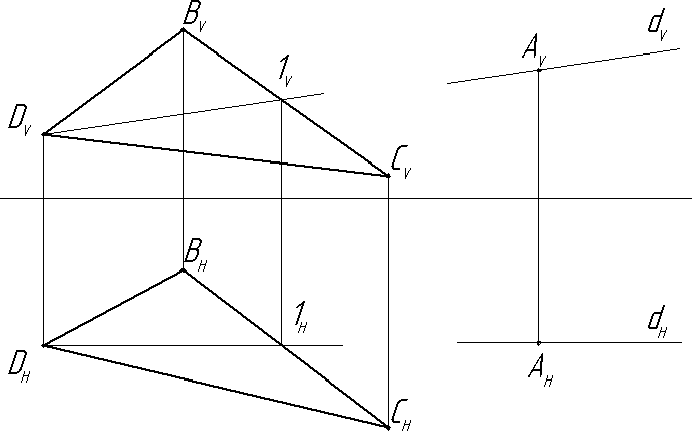
Рис. 3.7. Прямая параллельная плоскости

3.6. Параллельные плоскости

Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны.

У параллельных плоскостей соответственно параллельны линии уровня, линии ската и следы.

Задача: Через точку К провести плоскость, параллельную данной, задать ее линией ската и горизонталью (Рис.3.8).

Решение.

Провести в плоскости горизонталь и перпендикулярную ей линию ската. Через точку К провести плоскость, заданную двумя пересекающимися прямыми, одна из которых параллельна горизонтали, а вторая – линии ската.

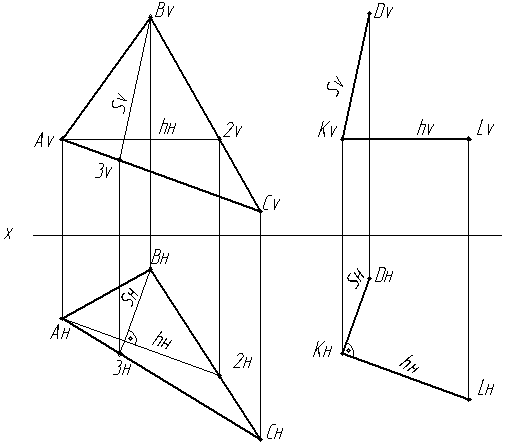
Рис. 3.8. Параллельные плоскости

3.7. Прямая, перпендикулярная плоскости

Прямая перпендикулярна к плоскости, если она перпендикулярна к двум пересекающимся прямым, принадлежащим плоскости.

Для того, чтобы на чертеже прямая была перпендикулярна к плоскости, согласно п.п. 2.4.1, необходимо, чтобы горизонтальная проекция прямой была перпендикулярна горизонтальной проекции горизонтали, а фронтальная проекция – к фронтальной проекции фронтали плоскости (Рис.3.9).

Рис.3.9. Перпендикулярность прямой и плоскости

Задача: Через точку К провести прямую, перпендикулярную плоскости треугольника АВС (Рис.3.10).

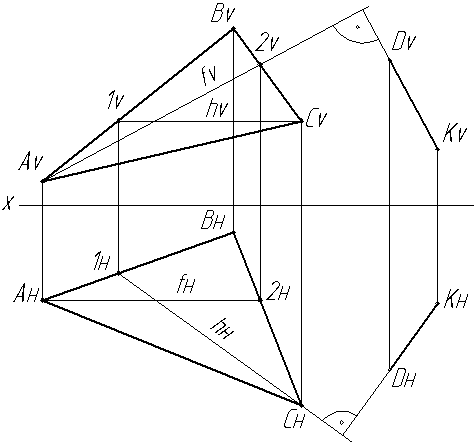
Рис. 3.10. Перпендикулярность прямой к плоскости

Решение.

В плоскости треугольника провести фронталь и горизонталь. Построить фронтальную проекцию прямой KD (К_vD_v) перпендикулярно к фронтальной проекции фронтали плоскости (А_v2_v), а горизонтальную проекцию прямой (K_нD_н) перпендикулярно проекции горизонтали (С_н1_н).

Задача: Определить расстояние от точки А до заданной плоскости (Рис.3.11).

Решение.

Чтобы найти расстояние от точки до плоскости, нужно из точки опустить перпендикуляр на плоскость, найти точку пересечения этого перпендикуляра с плоскостью и определить его натуральную величину.

Рис. 3.11. Определение расстояния от точки до плоскости