2.5. Ортогональные проекции плоскости

Плоскость представляет собой множество точек, которые при проецировании в общем случае покроют всю плоскость проекций, не давая на ней изображения. Поэтому плоскость в пространстве на проекциях определяют расположенные в ней элементы.

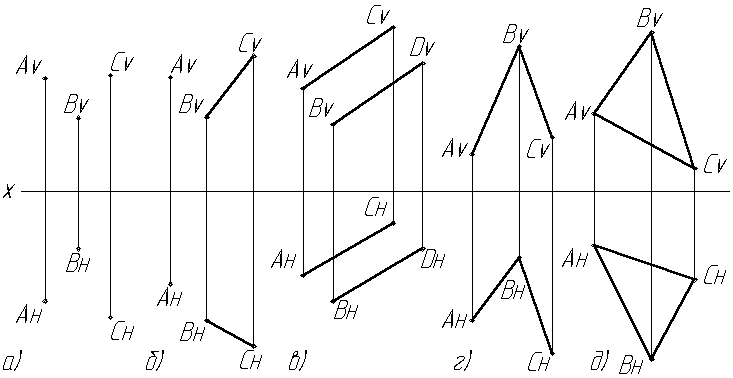
Рис. 2.14. Задание плоскости на эпюре

Такими элементами, определяющими плоскость, могут быть: три точки не лежащие на одной прямой (Рис.2.14а), прямой и не принадлежащей ей точки (Рис.2.14б), две параллельные прямые (Рис.2.14в), две пересекающиеся прямые (Рис.2.14г), плоская фигура (Рис.2.14д).

Кроме этого плоскость может быть задана следами (Рис.2.15а, б).

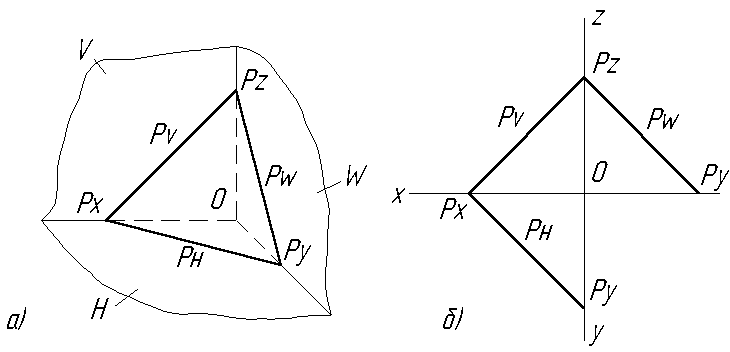
Рис. 2.15. Задание плоскости следами:

А) в диметрии; б) на эпюре

Прямые, по которым данная плоскость пересекается с плоскостями проекций называются следами плоскости. Р_н – горизонтальный след, Р_v – фронтальный след и Р_w – профильный след.

Точки Р_X, Р_Y, Р_Z называются точками схода следов.

2.5.1. Прямая и точка в плоскости

Задание плоскости на чертеже любым из перечисленных способов единственным образом определяет проекции всех точек и прямых, принадлежащих плоскости.

Прямая CD, проходящая через две точкиC и D, лежащие в плоскости, заданной прямымиАВиCD, принадлежит этой плоскости (рис.2.16).

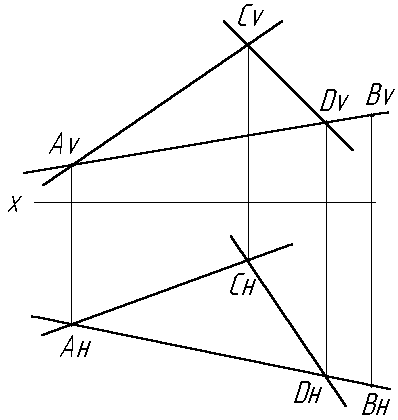
Рис. 2.16. Принадлежность прямой плоскости

Точка принадлежит плоскости, если через нее можно провести в этой плоскости прямую. Если точка М принадлежит плоскости АВС (Рис.2.17а, б), то по одной заданной проекции М_н можно определить другую проекцию М_v и притом единственную.

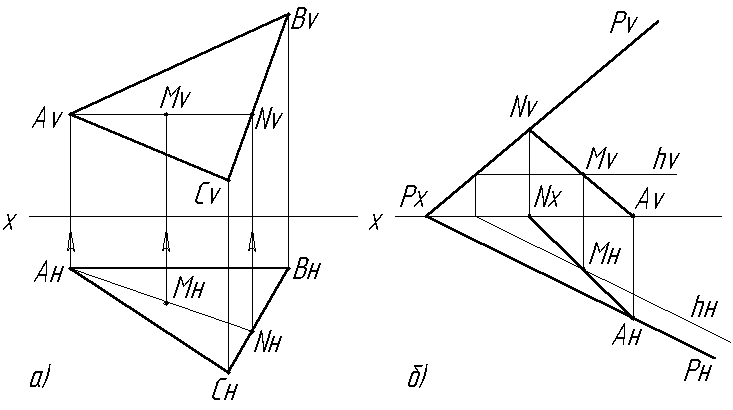
Рис. 2.17. Принадлежность точки плоскости:

А) заданной прямоугольником; б) заданной следом

Для этого через точку М (М_н) проведем какую-либо прямую АN (A_нN_н), принадлежащую данной плоскости; по линиям связи найдем вторую проекцию прямой (А_vN_v) и на ней соответствующую точку М_v.

В качестве такой вспомогательной прямой часто берут линии уровня, лежащие в данной плоскости.

2.5.2. Особые линии плоскости

К особым линиям плоскости относятся горизонталь плоскости, фронталь плоскости и линии наибольшего наклона к плоскости Н (линия ската).

Горизонталь плоскости – это прямая, лежащая в плоскости и параллельная плоскости Н (Рис.2.18а, б).

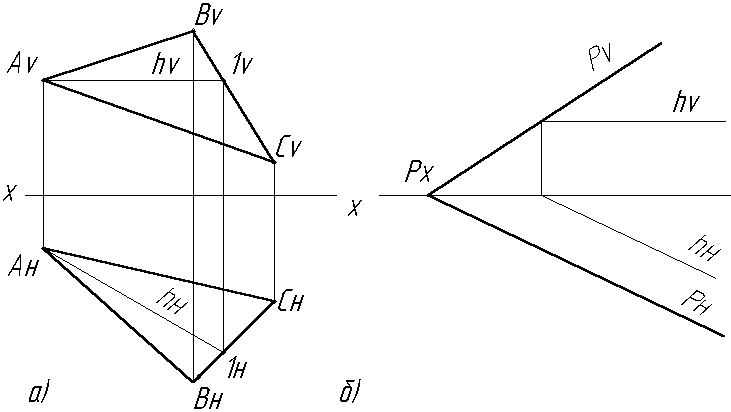
Рис 2.18 Горизонталь плоскости

Фронталь плоскости – прямая, лежащая в плоскости и параллельная плоскости V (Рис.2.19а, б).

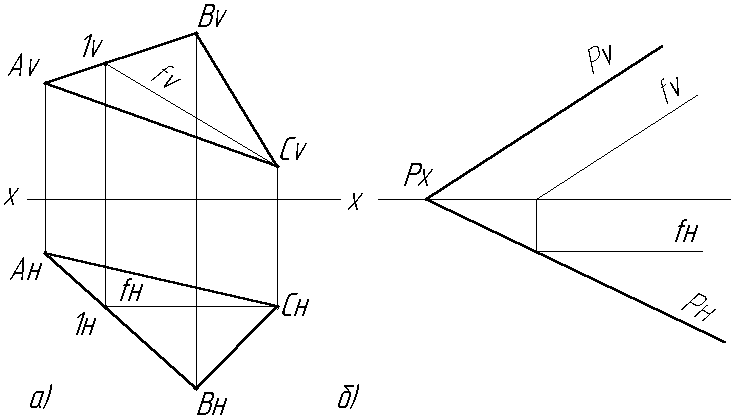
Рис 2.19 Фронталь плоскости

Линия ската S плоскости – это прямая, лежащая в плоскости и перпендикулярная к горизонтали плоскости (Рис.2.20а, б). Линия ската определяет угол наклона  плоскости к плоскости проекции Н.

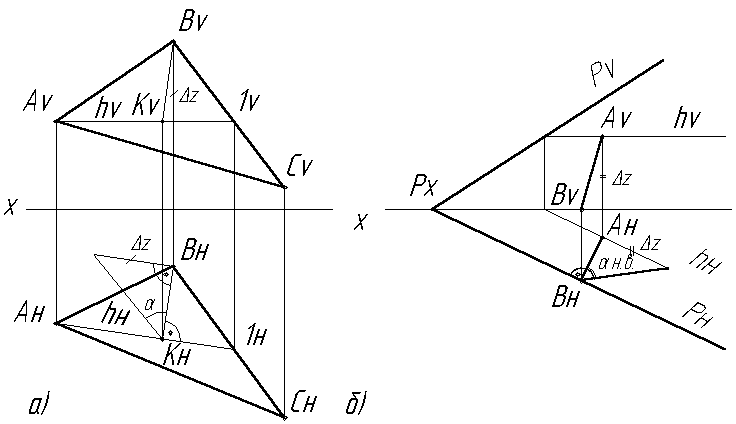
Рис. 2.20 Линии ската плоскости:

а)S =ВК в плоскости АВС;

б) S=АВ в плоскости заданной следами Р_Vи Р_H

Плоскость на чертеже может быть задана линией ската и горизонталью (как двумя пересекающимися прямыми). Этот способ является рациональным, т.к. достаточно задать положение линии ската, а горизонталь строится перпендикулярно к ней.

2.5.3. Плоскости общего положения

Плоскости не параллельные и не перпендикулярные ни одной из плоскостей проекций называются плоскостями общего положения. Такие плоскости изображены на рис. 2.14а, б, в, г, д.

2.5.4. Плоскости частного положения

К плоскостям частного положения относятся плоскости, перпендикулярные плоскостям проекций – проецирующие плоскости.

Такая плоскость проецируется в прямую линию на ту плоскость проекций, к которой она перпендикулярна. На этой прямой лежат проекции всех точек, линий и фигур, принадлежащих данной проецирующей плоскости (Рис.2.21а, б).

Проецирующая плоскость вполне определяется той своей проекцией, на которой она проецируется в линию (Рис.2.22а, б, в).

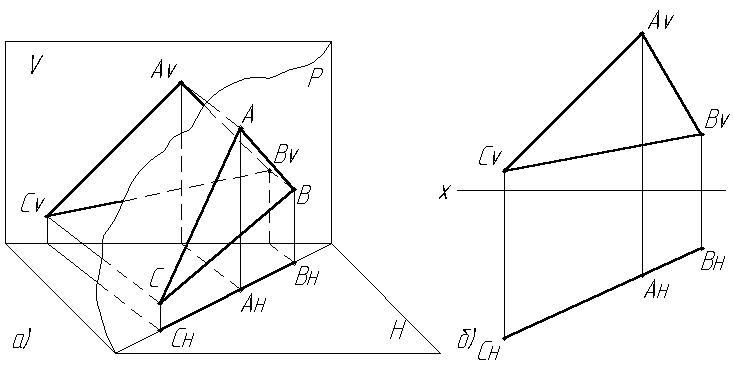
Рис. 2.21. Проецирующая плоскость: