Методические указания к выполнению контрольной работы № 3 Электростатика, постоянный ток Основные законы и формулы

1. Закон Кулона

,

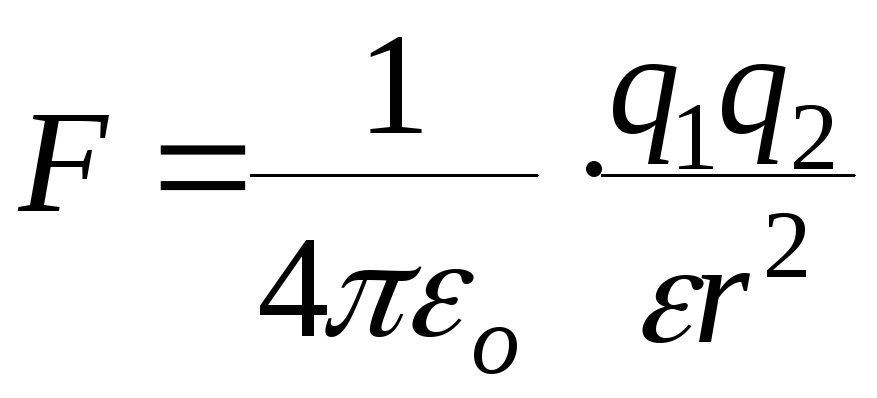где F- сила взаимодействия точечных зарядов q₁ и q₂, r- расстояние между зарядами, ε - относительная диэлектрическая проницаемость среды, ε_о- электрическая постоянная (ε_о= 8,85 ^. 10^-12 Ф/м).

2. Напряжённость и потенциал, электрического поля

где - сила, действующая на точечный положительный зарядq, поме­щённый в данную точку поля,

W- потенциальная энергия этого заряда ( при условии, что потенциальная энергия заряда удалённого в бесконечность, равна нулю).

3. Напряжённость и потенциал поля создаваемого системой точечных зарядов (принцип суперпозиции электрических полей)

, ,

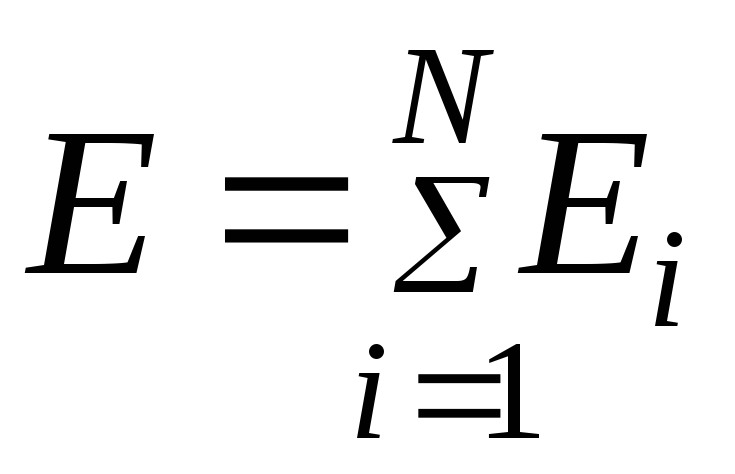где и- напряжённость и потенциал, соответственно, в данной точке поля создаваемогоi-м зарядом.

4. Напряжённость и потенциал поля, создаваемого точечным зарядом,

, ,

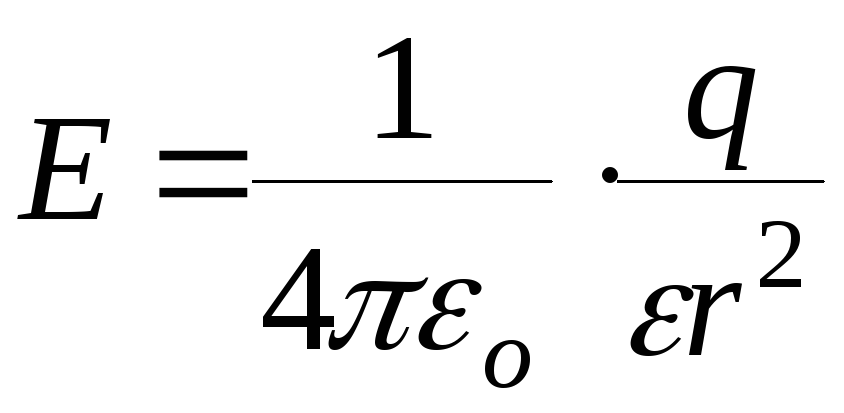где r расстояние от заряда q до точки, в которой определяются напря­жённость и потенциал.

5. Напряжённость поля, создаваемого бесконечной равномерно заряжен­ной плоскостью

,

где - поверхностная плотность заряда.

6. Напряжённость поля, создаваемого бесконечной равномерно заряжен­ной нитью, или бесконечно длинным цилиндром,

,

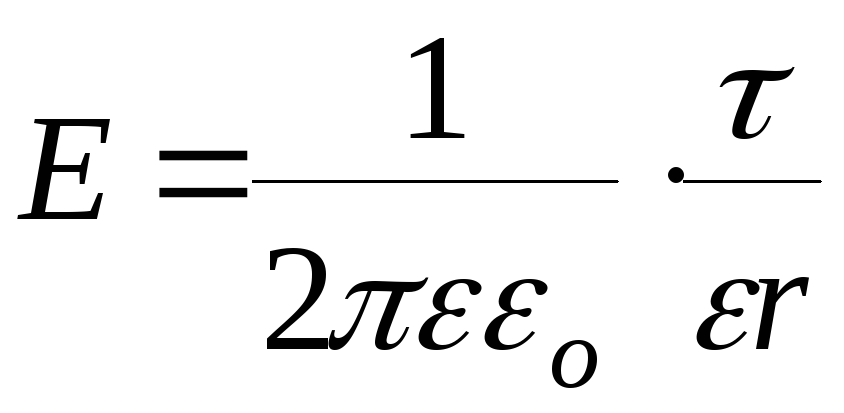где - линейна плотность заряда,

r- расстояние от нити или от оси цилиндра до точки, в которой вычисля­ется напряжённость.

7.Напряжённость и потенциал поля, создаваемого металлической заря­женной сферой радиусом R на расстоянии r от центра сферы:

а) внутри сферы ()

,

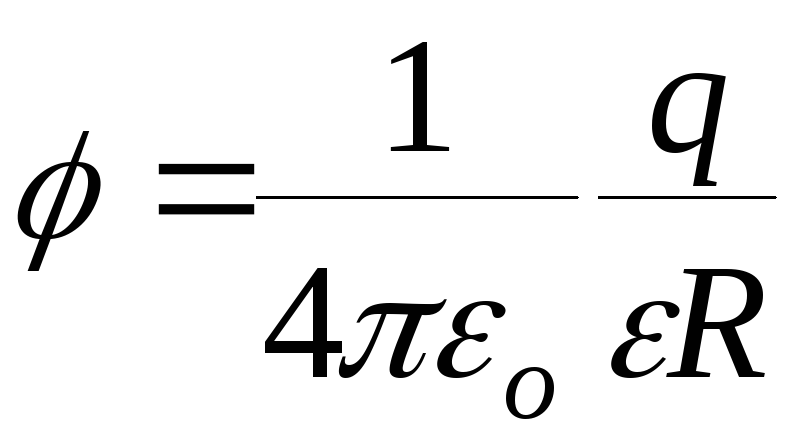б) вне сферы ()

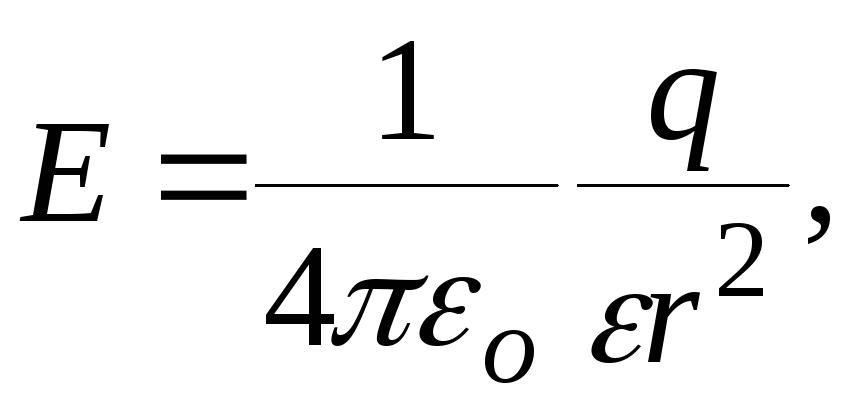
где q заряд сферы.

8.Напряжённость и потенциал поля, создаваемого распределёнными зарядами. Если заряд равномерно распределён вдоль линии с линей­ной плотностью , то на линии выделяется малый участок длинойdt с зарядом Такой заряд можно рассматривать как точеч­ный и применять формулы:

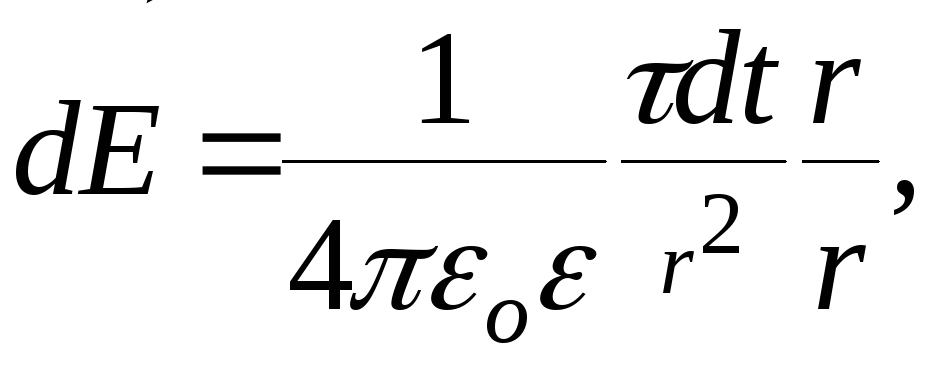
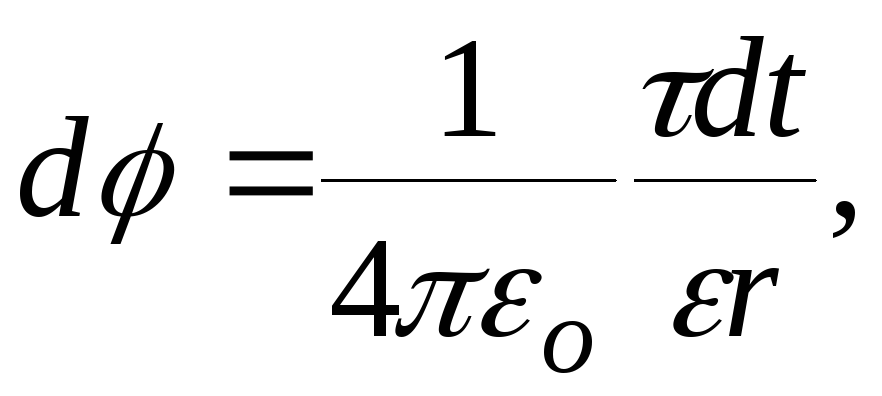
где - радиус –вектор, направленный от выделенного элемента к точке, в которой вычисляется напряжённость.

Используя принцип суперпозиции электрических полей, напряжённость и потенциалполя, создаваемого распределённым зарядом, нахо­дим интегрированием.

9. Связь потенциала с напряжённостью:

а ) в общем случае

;

б) в случае однородного поля

,

где d расстояние между точками с потенциалами и.

10. Работа сил поля по перемещению точечного заряда q из точки поля с потенциалом в точку поля с потенциалом

11. Поток векторов напряжённости и электрического смещения (индукции):

а) Через произвольную поверхность S, помещённую в неоднородное поле

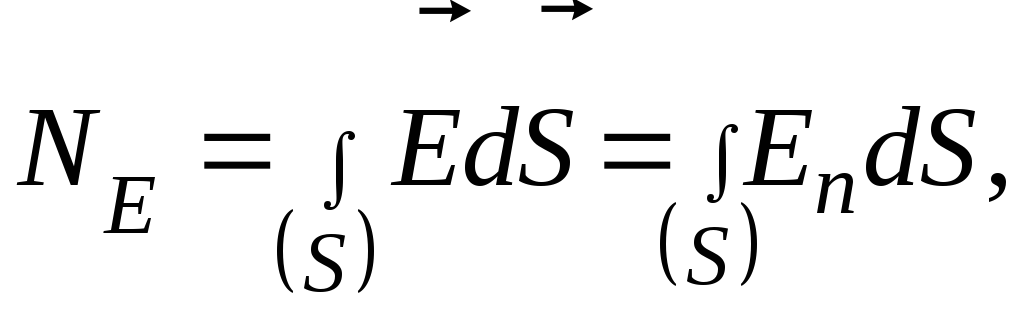
где ,- единичный вектор нормали к элементу поверхно­стиdS,

и - проекции векторовина направлении нормали,

- угол между вектором ии нормалью.

б) через плоскую поверхность, помещённую в однородное поле

.

12. Поток вектора ичерез любую замкнутую поверхность ( теорема Гаусса для поля в вакууме)

,

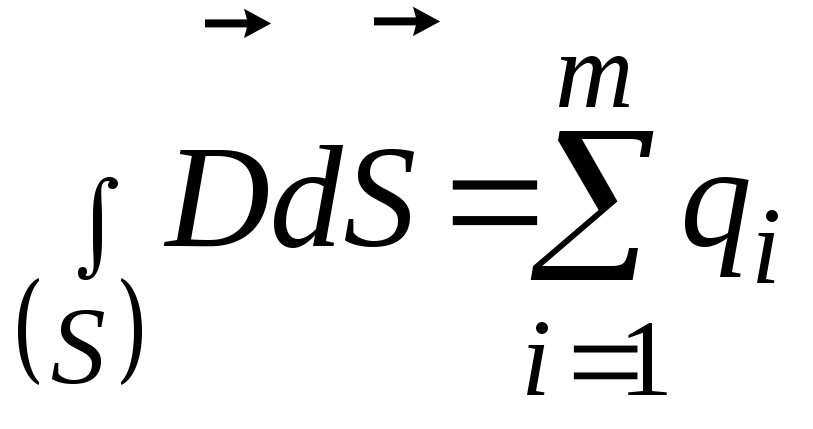где - алгебраическая сумма зарядов, заключенных внутри замкнутой поверхностиS, m- число зарядов.

13. Вектор электрической индукции ( смещения)

где - поляризованность (вектор поляризации).

14. Связь электрического смещения (индукции) с напряжённо­стьюв случае изотропных диэлектриков

.

15. Поверхностная плотность связанных поляризованных заря­дов на границах диэлектрика

,

где - проекция вектора поляризации на нормаль к поверхности диэлектрика,- угол между вектороми нор­малью.

16. Электроёмкость

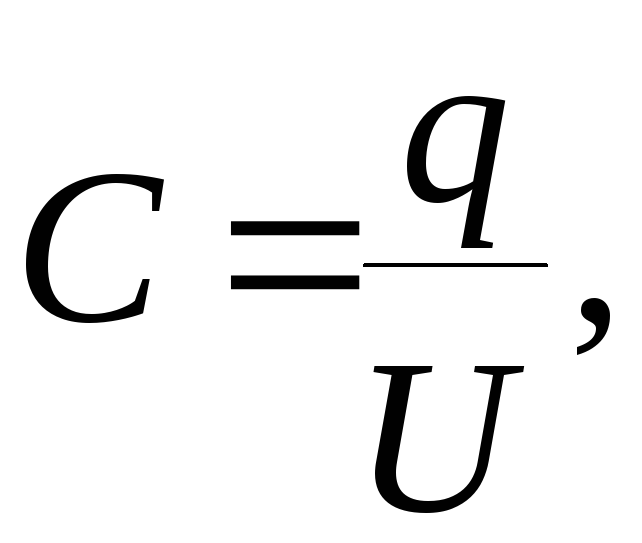
где потенциал уединённого проводника (при условии, что в бес­конечности потенциал проводника равен нулю),разность потенциалов между пластинами конденсатора.

17. Электроёмкость плоского конденсатора

где S – площадь пластины (одной) конденсатора, d – расстояние между пластинами, диэлектрическая проницаемость среды, заполняющей про­странство между пластинами.

18. Электроёмкость батареи конденсаторов

а) при параллельном соединении

,

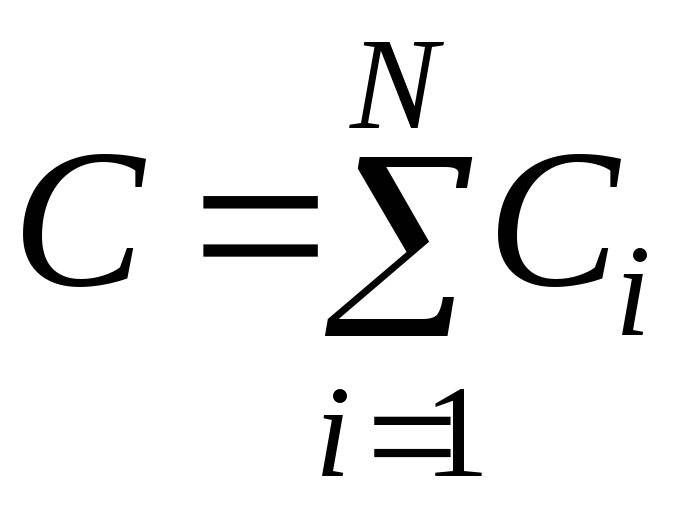б) при последовательном соединении

,

где N – число конденсаторов в батарее.

19. Энергия заряженного конденсатора

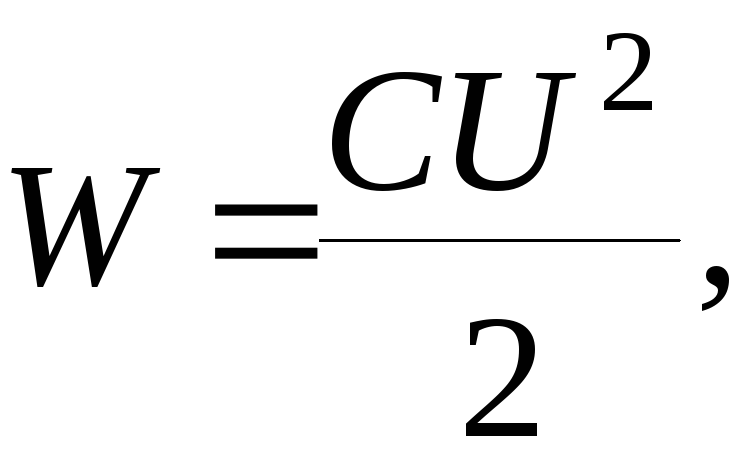
20. Объёмная плотность энергии электрического поля

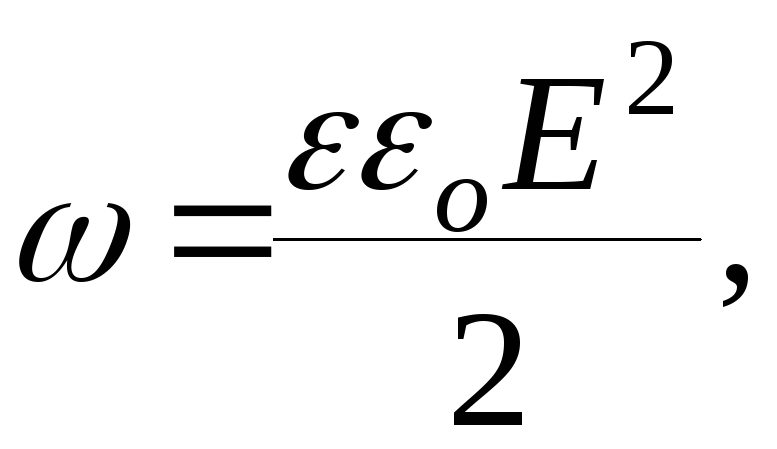
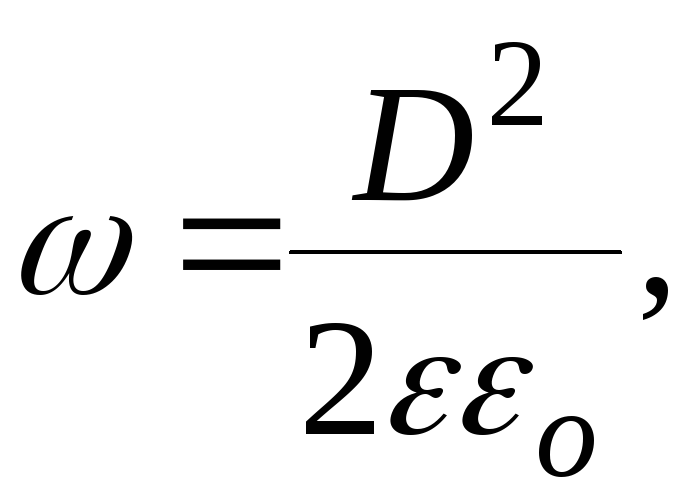
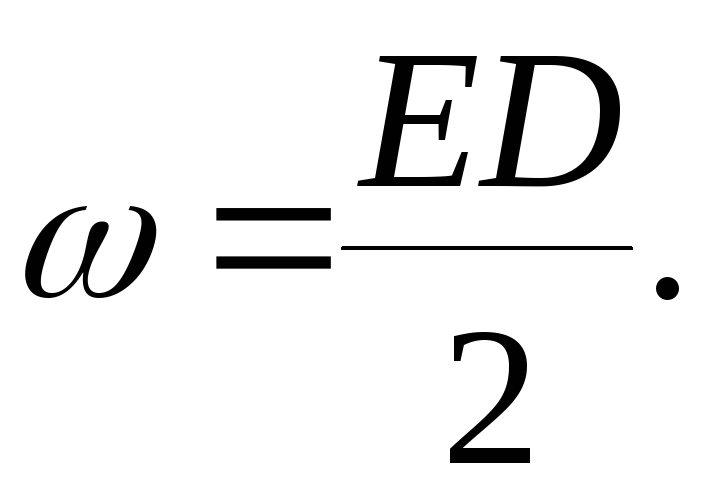
21. Закон Ома

а) для участка цепи, не содержащего ЕДС

,

где I – сила тока, - разность потен­циалов на концах участка цепи,R- сопротивление участка цепи,

б) для замкнутой цепи

,

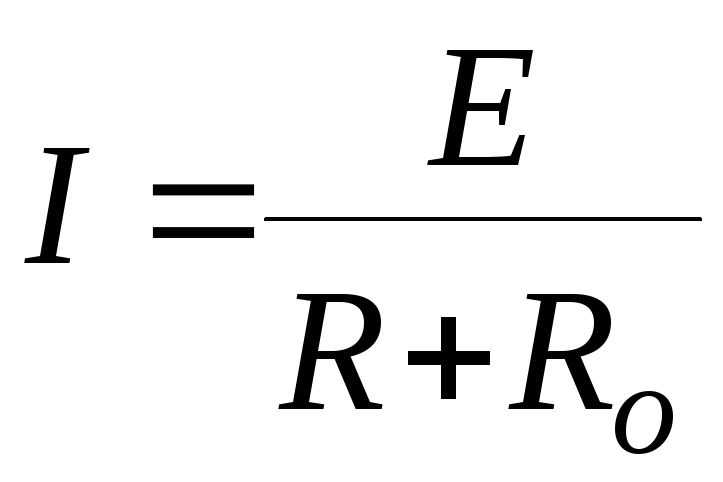где Е – ЭДС источника тока, R- сопротивление цепи, R₀ – внутреннее сопротивление источника тока.

22. Сопротивление R и проводимость G однородного проводника

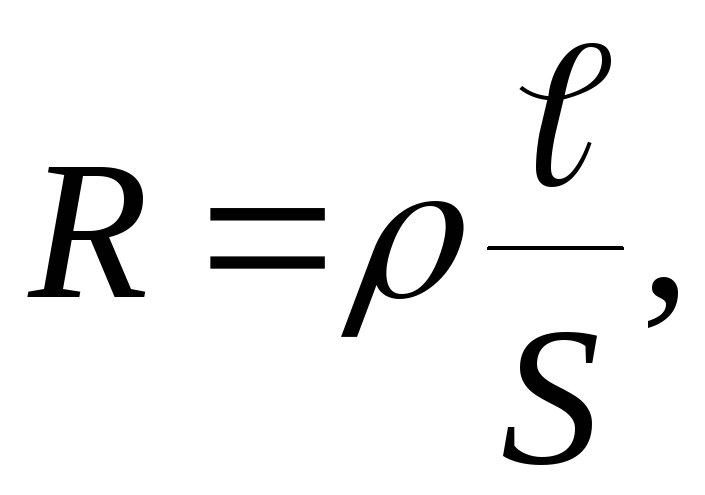
где - удельное сопротивление,удельная проводимость,длина проводника,S – площадь поперечного сечения проводника.

23. ЭДС и внутреннее сопротивлениебатареиn одинако­вых элементов:

а) при последовательном соединении

б) при параллельном соединении

,

где - ЭДС и- внутреннее сопротивление отдельного элемента.

24.Законы Кирхгофа:

а) 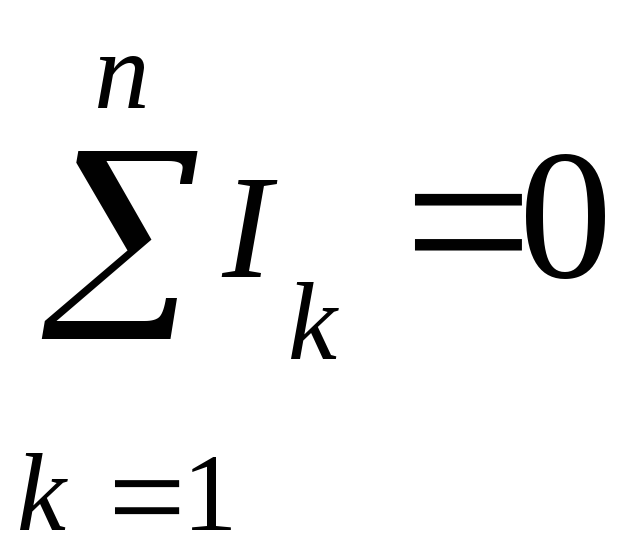(первый закон),

б) 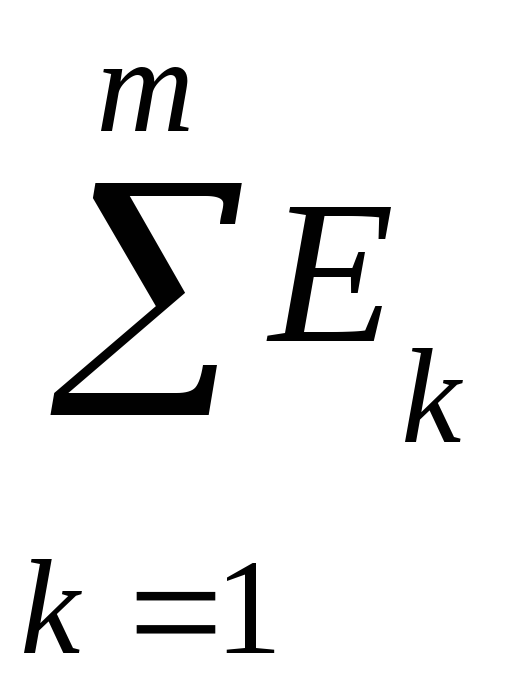(второй закон),

где 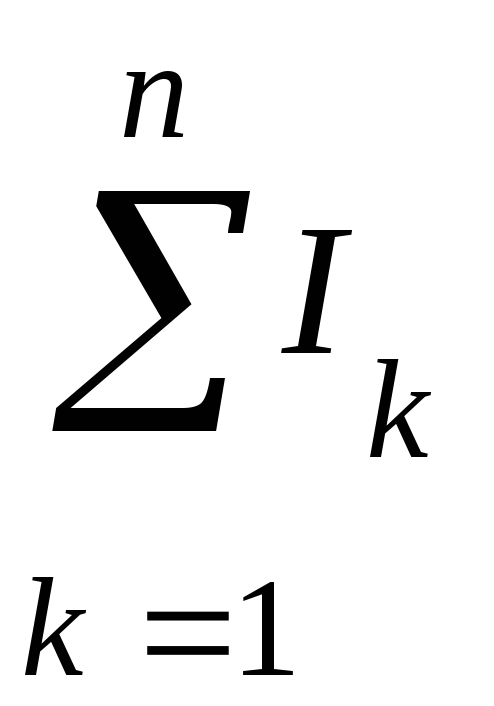алгебраическая сумма сил токов, сходящихся в узле,

алгебраическая сумма произведений сил токов на сопротив­ления участков цепи,

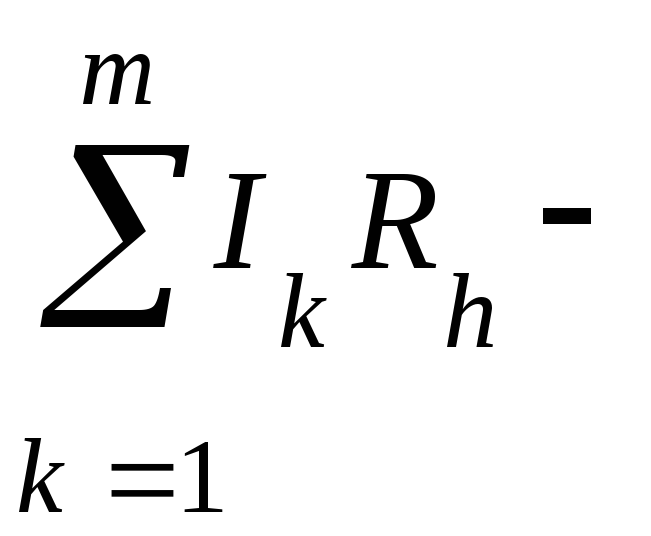алгебраическая сумма ЭДС, встречающихся в замкнутом контуре.

25. Работа и мощность тока

.

26.Закон Джоуля - Ленца

где Q – количество теплоты, выделяющейся на участке цепи сопротивле­нием R за время t.

27. Закон Ома в дифференциальной форме

,

где плотность тока,- напряжённость электрического поля,- удельная проводимость.

28.Закон Джоуля - Ленца в дифференциальной форме

,

где - объёмная плотность тепловой мощности тока.