Контрольная работа № 3

301. Два шарика с массами m=0,1г каждый подвешены в одной точке на нитях длиной каждая. Получив одинаковый заряд, ша­рики разошлись так, что нити образовали между собой угол. Найти заряд каждого шарика.

302. Два точечных заряда инаходятся в воздухе на расстоянииd=5 см друг от друга. Определить силу, действующую на заряд , удалённый от первого заряда на расстояниеи от второго заряда на расстояние

303. На продолжении оси тонкого прямого стержня, равномерно заря­женного с линейной плотностью заряда на расстоянииот конца стержня находится точечный за­рядВторой конец стержня уходит в бесконечность. Оп­ределить силу взаимодействия стержня и точечного заряда.

304. Когда два одинаковых шара массой подвешенные на закреплённых в одной точке нитях равной длины, зарядили одноимёнными зарядами, эти шарики разошлись на расстояниедруг от друга, причём нити образовали прямой угол. Найти заряд каждого шарика.

305. Четыре одинаковых точечных заряда закреплены в вершинах квадрата со сторонойНайти силу, действующую на один из зарядов со стороны трёх остальных.

306. Три одинаковых точечных заряда находятся в вершинах равностороннего треугольника со сторонойНайти силу, действующую на один из зарядов со стороны двух остальных.

307.Тонкий прямой стержень длиной равномерно заряжен. На продолжении оси стержня на расстоянии а=10см от его ближайшего конца находится точечный зарядОпределить линейную плотность заряда на стержне, если сила взаимодействия стержня и точечного заряда

308. В вершинах правильного шестиугольника со стороной а=3см помещены друг за другом точечные заряды Найти силу, действующую на точечный заряд, который находится в центре шестиугольника, если величина заряда

309. К бесконечной равномерно заряженной вертикальной плоскости подвешен на нити одноимённо заряженный шарик массой m =30 мг и зарядом Сила натяжения нити на которой висит шарик,F = 0,6мН. Найти поверхностную плотность заряда на плоскости.

310. По поверхности катода электронной лампы, выполненной в виде тонкой металлической нити, длиной , равномерно распределён зарядИз средней части нити катода вырывается электрон. Определить силу, действующую на электрон в точке , отстоящей от оси нити катода на расстоянииr=1см.

311. Поверхностная плотность заряда бесконечно протяжённой вертикальной плоскости . К плоскости на нити подвешен заряженный шарик массойm=10г. определить заряд шарика, если нить образует с плоскостью угол .

312. Две длинные прямые параллельные нити находятся на расстоянии d=10 см друг от друга. На нитях равномерно распределены заряды с линейными плотностями и. Определить напряжённость электрического поля в точке, удалённой от первой нити на расстояниеr₁=6см и от второй на расстояние r₂=8см.

313. Определить напряжённость поля, создаваемого зарядом, равномерно распределённым по тонкому прямому стержню с линейной плотностью в точке, лежащей на продолжении оси стержня на расстоянии а=30 см от его конца. Второй конец стержня уходит в бесконечность. Найти также силу, действующую в этой точке на точечный заряд

314. В одной плоскости с очень длинной нитью, равномерно заряженной с линейной плотностью заряда перпендикулярно нити расположен тонкий стержень, длиной, по которому равномерно распределён зарядРасстояние от нити до ближайшего конца стержня а=24см. Найти силу, действующую на стержень.

315. В вершинах квадрата со стороной, а=20см расположены три положительных и один отрицательный заряд. Определить напряжённость и потенциал электрического поля в центре квадрата, если величина каждого заряда

316. По тонкому проволочному кольцу равномерно распределён заряд с линейной плотностью Найти напряжённость и потенциал электрического поля в центре кольца.

317. В вершинах правильного шестиугольника со стороной а=10см находятся точечные заряды одинаковой величины Найти напряжённость и потенциал электрического поля при условии, что

а) знаки всех зарядов одинаковы;

б) знаки соседних зарядов противоположны.

318. На тонком прямом стержне длиной равномерно распределён зарядНайти напряжённость и потенциал электрического поля в точке, лежащей на продолжении оси стержня на расстоянии а=10см от его конца.

319.Тонкий стержень согнут в кольцо радиусом R=10 см. Стержень равномерно заряжен с линейной плотностью заряда Определить потенциал в точках, расположенных, на оси кольца на расстояниииот центра кольца.

320. В вершинах квадрата со стороной а=4см расположены друг за другом два положительных и два отрицательных заряда, величина каждого из них Определить напряжённость и потенциал электрического поля в центре квадрата.

321. По тонкому полукольцу равномерно распределён заряд с линейной плотностью. Определить напряжённость и потенциал электрического поля в точке, совпадающей с центром кольца.

322.Четверть тонкого кольца радиусом R=10 см равномерно заряжена с линейной плотностью заряда Определить напряжённость и потенциал электрического поля в точке, совпадающей с центром кольца.

323. Две бесконечные параллельные плоскости равномерно заряжены с поверхностной плотностью заряда и. Используя теорему Гаусса и принцип суперпозиции электрических полей, найти выражение для напряжённостиЕ поля между пластинами и вне пластин и построить график зависимости Е(х), где х – расстояние, отсчитываемое вдоль оси, перпендикулярной плоскостям. Найти разность потенциалов между плоскостями, если расстояние между ними d=3 см.

324. Решить предыдущую задачу при условии, что заряд второй пластины отрицательный.

325. Две концентрические металлические сферы радиусом R₁=6 см и R₂=10 см несут заряды иИспользуя теорему Гаусса, найти зависимость Е(r) напряжённости электрического поля от расстояния для тёх областей внутри первой сферы, между сферами и вне сферы. Найти напряжённость поля в точках, отстоящих от центра сфер на расстояние r₁=5 см, r₂= 9 см, r₃₌15см и построить график Е(r).

326. В однородном электрическом поле с напряжённостью Е₁=1кВ/м, переместили заряд в направлении силовой линии на расстояниеd=2см. Найти работу сил поля, изменение потенциальной энергии заряда и разность потенциалов между начальной и конечной точками.

327. Линейная плотность заряда равномерно заряженной проволоки Определить диэлектрическую проницаемость среды, если разность потенциалов двух точек поля, отстоящих от проволоки на расстояниеr₁₌1см и r₂₌2,72 см, равна .

328.Электрическое поле создано заряженным проводящим шаром, потенциал которого . Определить работу сил поля по перемещению зарядаиз точки находящейся на расстоянииr₁₌2R от центра шара в точку, находящуюся на расстоянии r₂₌3R (R- радиус шара).

329. Вблизи бесконечной равномерно заряженной плоскости находится точечный заряд Под действием сил электрического поля заряд переместился вдоль силовой линии на расстояние; при этом совершается работаНайти поверхностную плотность заряда плоскости.

330. На расстоянии r = 2см от бесконечно длинной заряженной нити находится точечный заряд Под действием сил поля заряд переместился до расстоянияr₂₌4 см, при этом совершается работа Найти линейную плотность заряда нити.

331. Тонкий стержень согнут в полукольцо. Стержень, равномерно заряжен с линейной плотностью заряда Какую работу надо совершить, чтобы перенести точечный зарядq = 6,7нКл из центра кривизны полукольца в бесконечность?

332. Какая работа совершается при перемещении точечного заряда из бесконечности в точку, находящуюся на расстоянии а=2см от поверхности сферы радиусомR=1 см равномерно заряженной с поверхностной плотностью заряда

333. Электроды двухэлектродной лампы (диода) имеют форму нити радиусом R₁=0,1 мм (катод) и коаксиального с ней цилиндра радиусом R₂=2,72 мм (анод). На электроды подано напряжение . Найти силу, действующую на электрон, находящийся от оси катода на расстоянииr ₌ 1мм.

334. Плоская квадратная пластина со стороной, а = 10см находится на некотором расстоянии от бесконечной равномерно заряженной () плоскости. Плоскость пластины составляет уголс линиями поля. Найти потокN электрического смещения через эту пластину.

335. В центре сферы радиусом R=20 см находится точечный заряд Определить потоквектора напряжённости через часть сферической поверхности площадью.

336. Бесконечная плоскость несёт заряд, равномерно распределённый с поверхностной плотностью . На некотором расстоянии от плоскости, параллельно ей, расположен круг радиусомR=10 см. Вычислить поток 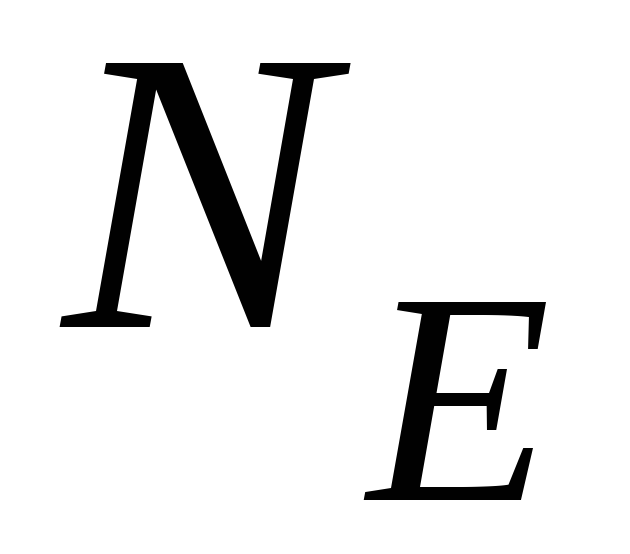вектора напряжённости и потоквектора индукции через этот круг.

337. Имеются две концентрические сферы радиусом R₁=10 см и R₂=20 см. Внутренняя сфера равномерно заряжена с поверхностной плотностью заряда . Определить потоквектора напряжённости через часть внешней сферической поверхности площадью.

338. Прямоугольная плоская площадка со сторонами а =3см и b=2 см находится на расстоянии r₌1см от точечного заряда Площадка ориентирована так, что линии напряжённости составляют уголс её поверхностью. Найти потоквектора напряжённости через площадку.

339. Электрическое поле создано двумя бесконечными параллельными плоскостями, равномерно заряженными с поверхностными плоскостями и. Между плоскостями находится плоская квадратная пластинка со стороной а = 10 см. Найти потоквектора индукции через пластинку, если её плоскость составляет угол= 30^о с линиями поля.

340. Бесконечная плоскость, равномерно заряженная с поверхностной плотностью заряда , пересекает сферу по диаметру (d =4cм). Найти поток электрического смещения через сферическую поверхность.

341. Две бесконечные параллельные плоскости, равномерно заряженные с поверхностными плотностями заряда и, пересекают цилиндрическую поверхность параллельно основаниям цилиндра. Найти потоквектора напряжённости через цилиндрическую поверхность, если радиус цилиндраR =2см.

342. Протон, обладающий кинетической энергией влетел в однородное электрическое поле в направлении силовых линий. Какой скоростью будет обладать протон, пройдя в этом поле разность потенциалов

343. Электрон вылетает из точки с потенциалом имея скорость, направленную вдоль силовой линии электрического поля. Определить потенциал точки поля, дойдя до которой электрон остановится.

344. Протон влетел в однородное электрическое поле с напряжённостью в направлении силовых линий со скоростьюКакой путь должен пройти протон, чтобы его скорость удвоилась?

345. Электрон, обладающий кинетической энергией , влетел в однородное электрическое поле в направлении силовых линий поля. Какой скоростью будет обладать электрон, пройдя в этом поле разность потенциалов?

346. Электрон с энергией (в бесконечности) движется вдоль силовой линии по направлению к поверхности металлической заряженной сферы радиусомR= 5cм. Определить минимальное расстояние, на которое приблизится электрон к поверхности сферы, если её заряд

347. При радиоактивном распаде из ядра атома полония вылетает - частица со скоростьюНайти её кинетическую энергию и разность потенциалов электрического поля, в котором можно разогнать покоящуюся- частицу до такой же скорости.

348. Электрическое поле образовано равномерно заряженной бесконечно длинной нитью. Двигаясь под действием сил поля из точки, находящейся на расстоянии r₁₌1 см от нити, в точку на расстоянии r₂₌4 см от неё, - частица изменила свою скорость отдо. Найти линейную плотность заряда нити.

349. На два последовательно соединённых конденсатора ёмкостью иподано постоянное напряжениеОпределить заряд на пластинах каждого конденсатора.

350. Конденсатор ёмкостью был заряжен до напряженияПосле того как его соединили параллельно со вторым конденсатором, заряженным до напряжения, напряжение на нём изменилось доВычислить ёмкость второго конденсатора.

351. Коаксиальный электрический кабель состоит из центральной жилы и цилиндрической оболочки, между которыми находится изоляция с диэлектрической проницаемостью . Вывести формулу для ёмкости такого кабеля и найти ёмкость единицы длины кабеля (в микрофарадах на метр).

352. Определить, с какой поверхностной плотностью распределён заряд на пластинах плоского конденсатора ёмкостью , если расстояние между пластинамиd=2мм и пластины притягиваются друг к другу с силой .

353. Газоразрядный счётчик элементарных частиц состоит из трубки радиусом и натянутой по оси трубки нити радиусом. Длина счётчикаПоложив, оценить межэлектродную ёмкость.

354. Плоский воздушный конденсатор заряжен до разности потенциалов Площадь пластин, напряжённость поля в зазоре между ними

Определить поверхностную плотность заряда на пластинах, ёмкость и энергию конденсатора.

355. Два длинных провода радиусом расположены в воздухе параллельно друг другу. Расстояние между их осями Найти взаимную ёмкость проводов, приходящуюся на единицу их длины.

356. Плоский конденсатор заряжен до разности потенциалов Заряд каждой пластины, расстояние между пластинами Определить силу взаимного притяжения пластин и энергию конденсатора.

357. Энергия плоского слюдяного конденсатора разность потенциалов между обкладками, площадь пластин. Определить расстояние между обкладками, напряжённость поля и объёмную плотность энергии конденсатора.

358. Плоский конденсатор содержит слой слюды толщиной и слой парафинированной бумаги толщиной Определить напряжённость поля и падение потенциала в каждом из слоёв, если разность потенциалов между обкладками конденсатора

359. Площадь пластин плоского конденсатора , расстояние между пластинами Какова будет ёмкость конденсатора, если на нижнюю пластину положить лист эбонита толщиной

360. В электрическое поле () между пластинами плоского конденсатора после отключения его от источника напряжения помещена перпендикулярно линиям поля плоскопараллельная пластина из эбонита. Определить напряжённость и индукцию электрического поля внутри пластины, поляризованность диэлектрика и поверхностную плотность связанных зарядов на эбоните.

361. Плоский конденсатор заряжен до разности потенциалов Расстояние между пластинами , диэлектрик - стекло. Определить поверхностную плотность связанных поляризованных зарядов на стеклянной пластинке.

362. Пространство между пластинами плоского конденсатора заполнено трансформаторным маслом. Расстояние между пластинами Какое напряжение надо подать на пластины этого конденсатора, чтобы поверхностная плотность связанных поляризованных зарядов на масле была .

363. Плоский конденсатор, площадь каждой пластины которого заполнен двумя слоями диэлектрика: слоем парафинированной бумаги толщиной и слоем стекла толщиной Конденсатор заряжен до разности потенциалов Найти энергию конденсатора.

364. Два одинаковых источника тока соединены в одном случае последовательно, а в другом параллельно и замкнуты на внешнее сопротивление Ом. При каком внутреннем сопротивлении источника сила тока во внешней цепи будет в обоих случаях одинаковой?

365. В сеть напряжением подключили катушку сопротивлениеми вольтметр, соединённые последовательно. Показание вольтметраКогда катушку заменили другой, вольтметр показалОпределить сопротивление другой катушки.

366. Какое напряжение нужно подать на катушку, имеющую витков медного провода со средним диаметром витков , если допустимая плотность тока .

367. Дуговая лампа мощностью рассчитана на напряжениеЕе надо включить в сеть с напряжениемс помощью дополнительного сопротивления из никелиновой проволоки диаметром Найти длину проволоки.

368. Две группы из трёх последовательно соединённых элементов соединены параллельно. ЭДС каждого элемента , внутреннее сопротивлениеПолученная батарея замкнута на резистор сопротивлениемНайти силу тока во внешней цепи и напряжение на резисторе.

369. ЭДС аккумулятора автомобиля . При силе токаего КПДОпределить внутреннее сопротивление аккумулятора.

370. ЭДС батареи . Наибольшая сила тока, которую может дать батарея. Определить максимальную мощность, которая может выделиться во внешней цепи.

371. Двигатель мощностью рассчитанный на напряжениенеобходимо подключить к источнику тока, составленному из элементов с ЭДСи внутренним сопротивлениемСколько элементов следует включить в цепь последовательно?

372. В алюминиевом проводнике объёмом при прохождении по нему постоянного тока за времяt=5 мин выделилось количество теплоты Вычислить напряжённость электрического поля в проводнике.

373. В медном проводнике длиной и площадью поперечного сечениятечёт ток. При этом ежеминутно () выделяется количество теплотыКакова плотность тока в проводнике?

374. Сила тока в проводнике сопротивлением Ом за времяt =30с равномерно нарастает от до. Определить количество теплотывыделившейся за это время в проводнике.

375. В проводнике за время при равномерном возрастании силы тока отдовыделилось количество теплотыНайти сопротивление проводника.

376. Сила тока в проводнике равномерно увеличивается от нуля до некоторого максимального значения в течение времени t = 20с. За это время в проводнике выделилось количество теплоты Определить скорость нарастания токав проводнике, если его сопротивлениеОм.

377. Сила тока в цепи изменяется со временем по закону Определить количество теплоты, которое выделится в проводнике с сопротивлениемОм за время, равное четверти периода (отдо, если период Т=4с.

378. Сила тока в проводнике сопротивлением Ом равномерно возрастает отдо некоторого максимального значенияв течение времениt=15с. За это время в проводнике выделилось количество теплоты Найти среднюю силу токав проводнике за этот промежуток времени.

379. По проводнику сопротивлением Ом течёт равномерно возрастающий ток. За время отв проводнике выделилось количество теплотыОпределить заряд, прошедший за это время, если начальный ток в проводнике был равен нулю.

380. Сила тока в проводнике изменяется со временем по закону , где. Определить количество теплоты, выделившейся в проводнике сопротивлениемОм за время

ЛИТЕРАТУРА

№	Основная
1	Трофимова Т.И. Курс физики: Учебное пособие для вузов/Т.И.Трофимова-13-е изд., стер. - М. :Академия., 2007.-560с. – ISBN5-7695-3662-4.
2	Трофимова Т.И. Курс физики: Учебное пособие для студ. вузов /Т.И.Трофимова-15-е изд., стер. - М. :Академия, 2007.-560с. – ISBN978-5-7695-45.
3	Хорошавина С.Г. справочник по физике /C.Г. Хорошавина. – Ростов-на-Дону: Феникс, 2002.-370 с.-(Учебники, учебные пособия).
4	Трофимова Т.И. Курс физики: Учебное пособие для вузов/Т.И.Трофимова-7-е изд., стер. - М. :Высшая школа., 2003.-542с.:ил.
5	Трофимова Т.И Сборник задач по курсу физики для втузов: Учебное пособие для студентов вузов/ Т.И.Трофимова.- 3-е изд. М.: ОНИКС 21 век, 2005.-384с.-ISBN5-329-01369-0.
6	Трофимова Т.И Физика. 500 основных законов и формул: Справочник /Т.И.Трофимова.-4-е. изд.-М.: Высш. шк. 2003.-62с
	Дополнительная
1	Фейнман Р., Лейтон Р., Сэндс М., Фейнмановские лекции по физике. М., Мир, 1965-1967, вып. 1-9.
2	Савельев И.В. Курс общей физики. М., Наука, 1982-1984, т. 1-3.
3	Матвеев А.Н. Курс общей физики. М, Высшая школа, 1976-1989, т. 1-У.
4	Астахов А.В., Широков Ю.М. Курс физики. М., Наука, 1977-1981, т. 1-3.
5	Орир Д. Физика. М., Мир, 1981, т. 1-2.
6	Кристи Р., Питти А. Строение вещества: введение в современную физику. М., Наука, 1969.
7	Мешков И.Н., Чириков Б.В. Электромагнитное поле. Новосибирск, Наука,1985, т.1-2.
8	Тарасов Л.В. Основы квантовой механики. М., Высшая школа, 1978.
9	Тарасов Л.В. Введение в квантовую оптику. М., Высшая школа, 1987.
10	Суханов А.Д. Лекции по квантовой физики. М., Высшая школа, 1991.
11	Киттель Ч. Введение в физику твердого тела. М., Наука, 1978.
12	Готтфрид К., Вайскопф В. Концепция физики элементарных частиц. М., Мир, 1988.
13	Иродов И.Е. Задачи по общей физике. М., Наука, 1987.
14	Савельев И.В. Сборник вопросов и задач по общей физике. М., Наука,1982.
15	Козел С.М., Рашба Э.И., Славатинский С.А. Сборник задач по физике. М., Наука,1987.

ПРИЛОЖЕНИЯ