Geodeziya_1_chastina_26-09-2011

Цю невизначену задачу (одне рівняння з трьома невідомими) можна зробити цілком визначеною, якщо її розв’язання підпорядкувати додатковій умові.

При обчисленні тріангуляції додаткова умова повинна бути такою, щоби одночасно з усуненням нев’язок ω отримати ймовірніше значення виміряних величин (максимально близьких до істинних). Найкраще така вимога виконується при застосуванні принципу найменших квадратів, згідно з яким сума квадратів шуканих поправок до безпосередньо і точно виміряних величин виявляється найменшою, тобто

Отже, сутність вирівнювальних обчислень тріангуляції полягає в усуненні незгод (нев’язок), які виникають у мережі, шляхом введення в результати безпосередніх вимірювань поправок, що визначаються способом найменших квадратів.

Вирівнювання тріангуляції із застосуванням принципу найменших квадратів здійснюється двома основними способами: способом умов і способом посередніх вимірювань.

При вирівнюванні способом умов складають так звані умовні рівняння, які відповідають геометричним умовам, що виникають у мережі. Доповнивши умовні рівняння вимогами (6.1), обчислюють поправки до результатів безпосередньо виміряних елементів тріангуляції, наприклад до напрямків або кутів.

При вирівнюванні способом посередніх вимірювань спочатку вибирають такі незалежні один від одного невідомі, через які можна виразити всі виміряні величини (їх називають необхідними невідомими). У цьому випадку видається можливим усі поправки виміряних величин замінити функціями незалежних невідомих, тобто отримати рівняння поправок, в яких невідомими служать вибрані не-

392

обхідні невідомі й поправки до результатів вимірювань. Розв’язуючи далі рівняння поправок під умовою

v2 min, знаходять як необхідні невідомі, так і поправки

до результатів вимірювань.

При обчисленні тріангуляції як необхідні величини звичайно використовують координати пунктів, тобто, як часто кажуть посередньо виміряні величини (функції безпосередньо виміряних величин). Так і отримав назву спосіб посередніх вимірювань.

Обидва ці способи, різні за формою, але тотожні між собою по суті, оскільки визначення невідомих поправок до виміряних величин в обох випадках виконується за принципом найменших квадратів.

12.2. Геометричні умови й умовні рівняння, які виникають у вільних мережах тріангуляції

Нехай на рис. 161 зображена вільна мережа тріангуляції, тобто така, в якій є тільки необхідні вихідні дані, наприклад координати пунктів А і В. Для більшої зручності і простоти викладення порядку складання геометричних умов і відповідних їм умовних рівнянь уведемо такі позначення:

Рис. 161. Вільна мережа тріангуляції

1, 2, 3,…,9 –

безпосередньо виміряні і приведені до площини значення кутів;

І, ІІ, ІІІ, …, ІХ – вирівняні значення відповідних кутів;

(1), (2), (3), …., (9) –

значення поправок

виміряних кутів;

393

S1, S2, S3 – вирівняні значення довжин сторін АО, ВО,

СО.

Користуючись прийнятими позначеннями, можна написати такі рівняння:

І = 1 + (1); ІІ = 2 + (2); (6.2)

………….

ІХ = 9 + (9).

Розглянемо геометричні умови, які виникають у даній мережі, і відповідні їм умові рівняння.

12.2.1. Умови фігур. Умовні рівняння фігур

Умови фігур виражають вимогу, щоби суми вирівняних значень кутів у трикутниках дорівнювали їх теоретичним значенням, тобто

де ω – нев’язка, створена помилками вимірювань кутів 1, 2 і 3. Щоби усунути нев’язку ω, необхідно виміряним кутам надати деякі поправки (1), (2) і (3), тобто врахувати (6.2), і

У способі найменших квадратів вираз (6.6) називається рівнянням поправок, сутність якого полягає в тому, що алгебраїчна сума поправок (1), (2) і (3) разом з нев’язкою повинна дорівнювати нулю. Аналогічно можуть бути написані умовні рівняння решти трикутників:

(4)+ (5) + (6) + ω2 = 0;

(7)+ (8) + (9) + ω3 = 0,

де ω2 = 4 + 5 + 6 – 1800; ω3 = 7 + 8 + 9 - 1800.

394

Вільні члени умовних рівнянь фігур трикутників, як і інших видів умовних рівнянь, є нев’язками (помилками), що обчислюються за правилом: «є − мінус − повинно бути».

12.2.2. Умова горизонту. Умовні рівняння горизонту

Умова горизонту містить вимогу, щоби сума вирівняних значень кутів, які не перекриваються і розташованих навколо однієї загальної вершини, дорівнювала 3600.

Отже, для кутів при точці О має бути дотримана геометрична умова

де ω0 – вільний член умовного рівняння горизонту, обчислений за формулою (6.8).

Якщо в тріангуляції кути вимірювалися способом кругових прийомів, то значення вільних членів умовних рівнянь горизонтів завжди дорівнює нулю. Але поправки у вирівнювальні кути цього рівняння можуть бути порушені, якщо умови горизонтів не будуть враховані. Тому умовні рівняння горизонтів і з вільними членами, що дорівнюють нулю, при вирівнюванні кутів повинні бути включені в систему умовних рівнянь обчислюваної тріангуляції.

395

12.2.3. Умова полюсів. Умовні рівняння полюсів

Умова полюса виникає у фігурі, яка має замкнутий ланцюг трикутників, наприклад у центральній системі, тобто в такій фігурі, де є ряд суміжних трикутників з загальною вершиною, основи яких створюють замкнуту фігуру. Загальна вершина таких суміжних трикутників називається полюсом, а замкнута фігура − основою полюса.

Геометрична умова полюса містить вимогу, щоби в замкнутій мережі трикутників довжина будь-якої сторони, обчислена від довільно обраної, але однієї і тієї ж сторони по вирівняних кутах різними шляхами, мала однакове числове значення.

Для мережі тріангуляції, зображеної на рис. 161, ця умова містить вимогу, щоби будь-яка сторона (S1, S2, S3, …) мала однакове значення при двох різних визначеннях. Так,

S3 AB sinsinIII sinsinVIIIX

при обчисленні її за вихідною стороною АВ через трикут-

ники АОВ і АОС,

S3 AB sinsinIIII sinsinVIIV .

При обчислені її за тією ж стороною АВ через трикутники АОВ і ОВС, які зв’язують загальну шукану сторону, повинні мати однакові числові значення.

Зазначені вище вимоги можна подати у вигляді рівнос-

ті

яка після перетворення буде мати вигляд

Цю ж умову полюса можна записати в логарифмічному вигляді

396

Оскільки як значення поправок (1), (2), (3), …, (9) звичайно бувають достатньо малими, до членів виразу (8.13)

…………………………..

lgsin 9 (9) lgsin 9 9 (9) ,

де β1, β2, …, β9 – зміни логарифмів синусів кутів, відповідно до змін самих кутів на 1".

Тоді рівняння (6.13) матиме вигляд

lgsin 2 2 (2) lgsin 7 7 (7) lgsin 4 4 (4)

lgsin 3 3 (3) lgsin 6 6 (6) lgsin 9 9 (9) 0

або

2 (2) 4 (4) 7 (7) 3 (3) 6 (6) 9 (9)

(lgsin 2 lgsin 4 lgsin 7) (lgsin 3 lgsin 6 lgsin 9) 0.

(6.15)

Унаслідок неминучих помилок вимірювань рівняння (6.12) не справдиться, якщо у нього підставити виміряні значення кутів. Практично отримаємо

(lg sin 2 lgsin 4 lgsin 7) (lgsin 3 lgsin 6 lgsin 9) 0 .

(6.16)

Враховуючи вирази (6.15) та (6.16), отримаємо умовне рівняння полюса, яке відповідає умові (8.12):

2 (2) 4 (4) 7 (7) 3 (3) 6 (6) 9 (9) 0 0, (6.17)

де 0 − вільний член умовного рівняння полюса, обчислений за формулою (6.16).

397

Значення коефіцієнтів β в умовних рівняннях полюсів або обираються з таблиць логарифмів, або обчислюються в одиницях того ж знака, що й обчислені вільні члени ω умовних рівнянь. Наприклад, якщо при врівноваженні тріангуляції 3-го і 4-го класів вільні члени обчислюються в одиницях шостого знака, тому і β повинні обиратися з таблиць в одиницях шостого знака логарифмів.

Знаки зміни логарифмів синусів кутів беруться додатними, якщо кути менші 90°, і від’ємними – при кутах, більших 90°, оскільки зі збільшенням кута в перший чверті його синус, а отже, й логарифм збільшуються, а в другій − зменшуються. Умовні рівняння полюсів можна доволі просто і зручно написати, користуючись схемою мережі. Робиться це так. Нумеруються по порядку всі зв’язкові кути, розташовані по контуру основи полюса. Потім, користуючись цією нумерацією, пишуть умови полюса за правилом: різниця сум логарифмів синусів непарних і парних зв’язкових кутів, розташованих при основі контуру, повинна дорівнювати нулю.

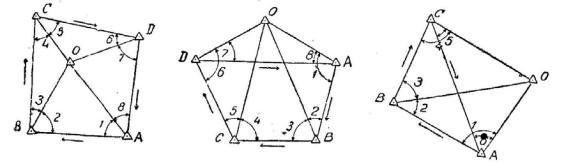
Рис. 162, 163, 164. Фігури тріангуляцій

Наприклад, для фігур тріангуляцій, зображених на рис. 162, 163 і 164, в яких полюси позначені літерою О, геометричні умови відповідно пишуться так:

(lgsin 2 lgsin 4 lgsin 6).

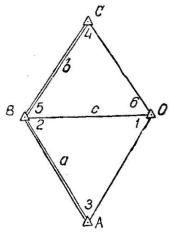
13.Геометричні умови і умовні рівняння, які виникають у невільних мережах тріангуляції

Рис. 165. Невільна мережа тріангуляції

Невільними мережами тріангуляції називаються такі мережі, в яких є надлишкові вихідні дані, наприклад мережа, зображена на рис. 165, в якій вихідними даними служать координати трьох пунктів А, В і С, замість необхідних двох.

399

У невільних мережах, окрім геометричних умов фігур, горизонту і полюса, виникають ще умови дирекційних кутів, базисів і координат.

13.1. Умови і умовні рівняння дирекційних кутів

Умови дирекційних кутів виникають у таких мережах тріангуляції, в яких вихідних дирекційних кутів більше, ніж необхідно, а позаяк для обчислення будь-якої тріангуляції необхідно і достатньо мати тільки один вихідний дирекційний кут, умови дирекційних кутів будуть виникати в усіх випадках, коли вихідних дирекційних кутів у мережі буде більше одного.

Геометрична умова дирекційних кутів виражає вимогу, щоби значення надлишково заданого дирекційного кута, обчислене за вихідним дирекційним кутом і врівноваженим значенням кутів, дорівнювало даному значенню цього дирекційного кута. Так, якщо в тріангуляції, зображеній на рис. 165, дирекційний кут (ВА) прийняти за вихідний, а дирекційний кут (ВС) – за надлишково наданий, то умову дирекційних кутів у цій тріангуляції можна записати так:

(ВС) = (ВА) – (ІІ + V)

де ωα – нев’язка, створена помилками вимірювань кутів 2 і 5.

Для усунення нев’язки ω виправимо виміряні кути

де ωα – вільний член умовного рівняння дирекційних кутів.