Geodeziya_1_chastina_26-09-2011

481

Довжини дуг A0B0 і AC пропорційні їх радіусам, причому радіус першої дорівнює радіусу кулі R, а другий (із

при центрі кулі, що відповідає дузі A0A = YA і виражений у радіальному вимірі.

Отже,

Помноживши чисельник і знаменник останнього виразу на

482

Y

членів другого порядку малості відносно R масштаб у

будь-якій точці у функції сферичної ординати на основі (7.8) визначиться формулою

зберігши члени четвертого порядку малості, то отримаємо

У формулах (7.9) і (7.10) Y – сферична ордината цієї точки і R – радіус кулі. Але сферичні прямокутні координати не мають застосування в практиці. Тому виразимо масштаб у функції плоскої ординати, для чого заздалегідь знайдемо залежність між сферичними прямокутними координатами X, Y точки на кулі і плоскими прямокутними координатами

483

Формулами (7.11) і (7.12) виражені умови побудови зображення в проекції Гаусса в аналітичній формі.

Щоб отримати плоскі координати, тобто відстані, наприклад, точки В до осей координат у функції сферичних координат, потрібно підсумовувати нескінченно малі відрізки, що складають ці відстані, за законами, вираженими рівняннями (7.11) і (7.12).

В результаті такого підсумовування отримаємо:

Підставимо тепер у формулу (7.10) значення Y з виразу (7.14). При цьому будемо утримувати члени до четвертого

нати в членах четвертого порядку рівними.

Тоді

звідки в остаточному вигляді отримаємо формулу масштабу зображення в проекції Гаусса у функції плоскої орди-

484

В межах шестиградусної зони член четвертого порядку не перевершить 1 : 5 000 000. Тому він враховується при редукуванні тільки базисів 1-го і 2-го класів; в усіх інших випадках користуються формулою

2.3.2. Перехід від відстаней на еліпсоїді до відстаней на площині

Геодезична лінія між двома точками на поверхні еліпсоїда, як уже зазначалося вище, зображається на площині в проекції Гаусса у вигляді кривої малого вигину з незначним відхиленням від хорди, що стягує її кінці. Тому практично можна вважати довжину плоскої кривої aa'b = s (рис. 178) рівною довжині хорди ab = D.

Проте відстань D між точками а(х1 у1) і b(х2, у2) на площині внаслідок неминучого спотворення довжин ліній, обумовленого проекцією, не дорівнюватиме відстані між відповідними точками на еліпсоїді (у натурі).

Для порівняно коротких відстаней (D ≤ 15 км) залежність між довжиною S лінії на еліпсоїді і довжиною D хорди на площині може бути виражена за допомогою масштабу зображення, який визначається формулою (7.16), а саме:

або

485

Рис. 178. Зображення геодезичних ліній на еліпсоїді і на площині

де ym 12 y1 y2 – середня ордината;

R MN – середній радіус кривизни в середній точці геодезичної лінії;

mm – масштаб проекції в середній точці геодезичної

лінії.

Отже, щоб перенести довжину лінії з еліпсоїда на площину в проекції Гаусса, її необхідно помножити на масштаб проекції в середній точці цієї лінії.

При обчисленнях зручніше отримувати не безпосередньо саму відстань D, а поправку D, яку належить додати до значення S, щоб отримати шукану відстань D. Тоді, згі-

дно з (7.17),

486

Різниця ∆D = D – S є шуканою поправкою в довжину лінії при перенесенні її з еліпсоїда на площину. Поправка завжди додатна, інакше кажучи, довжина хорди зображення геодезичної лінії на площині в проекції Гаусса завжди більше від довжини S самої лінії на еліпсоїді.

Формула (7.19) наближена, оскільки вона не враховує зміну масштабу в різних точках лінії. Обчислена по ній поправка ∆D при довжинах до 10 км матиме помилку 1 мм.

Точніша формула, що забезпечує обчислення поправки ∆D при довжинах до 25 км із помилкою близько 2–3 мм, має такий вигляд:

де ∆y = y2 – y1 – різниця ординат кінців лінії на площині. При обчисленні поправок за редукування коротких лі-

ній з невисокою точністю, наприклад 1 : 1000, значення R можна прийняти постійним, що дорівнює 6380 км. При цьому значенні радіуса і за умови, що довжина S лінії і середня ордината уm також виражені в кілометрах, формула (7.19) для обчислення шуканої поправки AD (у міліметрах) може бути написана так:

487

Щоб за допомогою цієї таблиці обчислити поправку на перенесення на площину лінії довжиною S, останню слід виразити в кілометрах і помножити на табличне значення ∆D, вибране для заданої ординати ym.

Нехай, наприклад, виміряна на місцевості і віднесена на поверхню референц-еліпсоїда довжина лінії S=1285,0 м; ордината ym середньої точки цієї лінії дорівнює 208 км. Тоді поправка D, що припадає на 1 км довжини і вибрана з таблиці лінійною інтерполяцією для ym = 208 км, дорівнюватиме 533 мм. Отже, шукана поправка ∆D на всю довжину лінії

∆D = 533 х 285 = 685 мм,

а довжина лінії, віднесена на площину в проекції Гаусса,

D = S + ∆D = 1285,0 + 0,7 = 1285,7 м.

З формули (7.19) видно, що спотворення відстаней у проекції Гаусса пропорційно квадрату віддалення середньої точки лінії від осьового меридіана.

На краях шестиградусної зони відносне спотворення відстаней не перевищує 1 : 1000. Тому редукціями для віднесення відстаней, виміряних за допомогою віддалеміра кіпрегеля по рейці, можна знехтувати.

2.4. Формули для обчислення поправок у напрямки на кривизну зображення геодезичних ліній на площині

Нехай на поверхні земного еліпсоїда дані точки А і В (рис. 179), між якими проведена геодезична лінія АВ, яка є, наприклад, стороною трикутника тріангуляції. З кінців цієї лінії проведемо геодезичні лінії АА0 і ВВ0, перпендикулярні до осьового меридіана ОР зони.

На площині в проекції Гаусса точки а і b, визначені відповідно координатами x1, y1 і x2, y2, є зображенням точок А і В еліпсоїда; пряма ох – проекція осьового меридіана ОР, а прямі аа0 і bb0 являють собою зображення геодезичних лі-

ній АА0 і ВВ0.

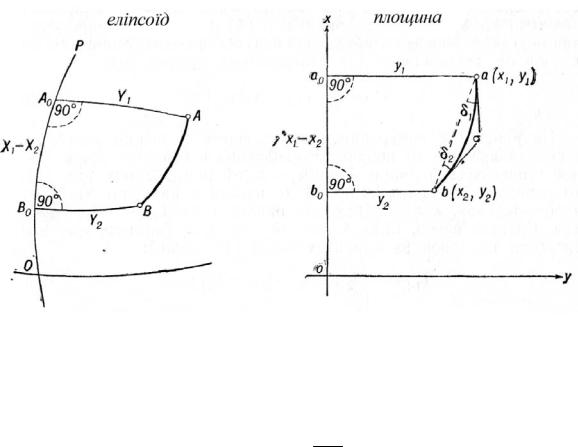
488

Оскільки в рівнокутній проекції кути зображуються без спотворень, то плоске зображення сфероїдичної трапеції АВВ0А0, тобто фігура aσbb0a0, повинна мати суму кутів, що дорівнює 360° + ε, де ε – сферичний надлишок фігури

АВВ0А0.

Звідси випливає, що геодезична лінія АВ зобразиться на площині деякої кривої aσb, угнутість якої буде обернена у бік осі абсцис. Очевидно, сума малих кутів δ1 і δ2, створених зображенням геодезичної лінії aσb із хордою ab, повинна дорівнювати сферичному надлишку ε трапеції АВВ0А0, тобто

ε=δ1+δ2 . (7.22)

Рис. 179. Абсолютна величина поправки δ за кривизну зображення геодезичної лінії на площині

де Р – площа сферичної фігури.

Для обчислення сферичного надлишку площу фігури АВВ0А0 з великим ступенем точності можна вважати та-

489

кою, що дорівнює площі плоскої трапеції abboao, обчисленій за формулою

динаті уm середньої точки хорди ab.

Підставивши значення Р, виражене формулою (7.24), в рівність (7.23), отримаємо

Абсолютні величини малих кутів δ1 і δ2, взагалі кажучи, різні. Проте при відносно невеликих відстанях між пунктами А і В, наприклад, при довжинах сторін трикутників тріангуляції до 10 км і ym<100 км, величини їх можна вважати рівними: δ1=δ2= δ. Тоді формула (7.25) для визначення величини кута δ між зображенням геодезичної лінії аσb і хордою ab, що стягує це зображення, набере вигляду

Поправки δ у виміряні напрямки – величини алгебраїчні, залежні від координат початкової і кінцевої точок даної геодезичної лінії. Якщо х1 – х2 >0 і ym >0 (див. рис. 4), то поправка δ1.2 напрямку аb (з пункту а на пункт b) буде додатна, а для зворотного напрямку δ2.1 – від’ємна. Отже,

прийнявши, що 1.2 2.1 , формула для обчислення поправок на кривизну буде такою:

1 2 2 1 2R2 x1 x2 ym,

Точніші формули, що забезпечують обчислення поправок δ з точністю 0",01 і вищі, такі:

з пункту ί на пункт k –

а для зворотного напрямку, тобто з пункту k на пункт ί,

Отже, в загальному випадку поправки δίk і δkі у взаємні напрямки протилежні за знаком і не дорівнюють один одному за абсолютною величиною, якщо yί ≠ yk.

При обчисленні поправок на кривизну зображення геодезичних ліній на площині в проекції Гаусса для виправлення кутів, виміряних із високою точністю (в державній геодезичній мережі), використовується формула (7.28). При менш точних роботах поправки δ обчислюють за фор-

мулою (7.27), вважаючи при цьому, що f = 0,0025 = 4001 .

У практиці поправки на кривизну знаходяться різними способами: аналітично, за допомогою таблиць і різного роду номограм.

Про знаки поправок δ можна судити не лише по знаках співмножників (x ί - xk) і (2y1+y2) або уm. Вони легко визначаються за орієнтованою схемою мережі, на якій між пунктами проведені криві Аσ1В, Аσ2С, ..., що являють собою зображення геодезичних ліній на площині, а отже, повер-