3. Знайти границю функції

4. Скласти рiвняння площини, яка проходить через пряму

пер пендикулярно до площини 3x − 2y + z = 0.

1. Степеневі ряди та область їх збіжності. Формула Коші-Адамара.

Оз. Степеневим рядом називається функціональний ряд виду

+ (1)

де , - постійні дійсні числа, які називаються коефіцієнтами степеневого ряду, а функцiональний ряд вигляду a_n(x - x ₀)ⁿ = a₀ + a₁(x- x₀) + a₂(x - x₀)² + …+ a_n(x - x₀)ⁿ + ...

називається степеневим рядом з центром в точцi x₀.

Всякий степеневий ряд збіжний в точці х = 0 до суми S = а. Тому область збіжності степеневого ряду завжди містить принаймні одну точку.

Оз. Множина тих x Є R, для яких ряд збiжний, називається областю збiжностi цього ряду.

Теорема Абеля. Якщо Степеневий ряд (1) збігається при х=х₀, то він абсолютно збігається для всіх х , що задовольняють умові . Якщо при х=х₀ степеневий ряд розбігається, то він розбігається і при всіх х, які задовільняють умову .

Теорема. Якщо існує ,то радіус збіжності степеневого ряду

Довед. Розглянемо ряд , складений з модулів його членів

(3)

Відомо, що якщо ряд (3) збігається, то буде збігатися і ряд (1), і при цьому абсолютно.

Нехай , 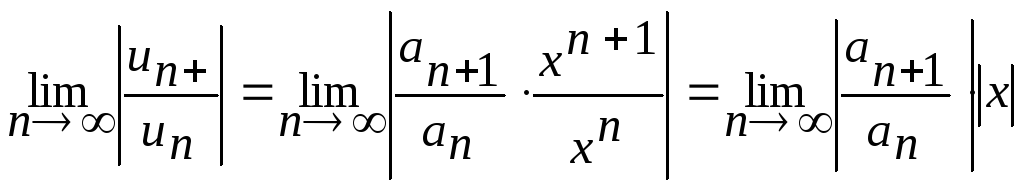.Згідно з ознакою вста Даламбера ряд (3) збігається, якщо , тобто, якщо ,і розбігається, якщо .Отже, степеневий ряд (1) збігається, для всіх тих значень х, для яких 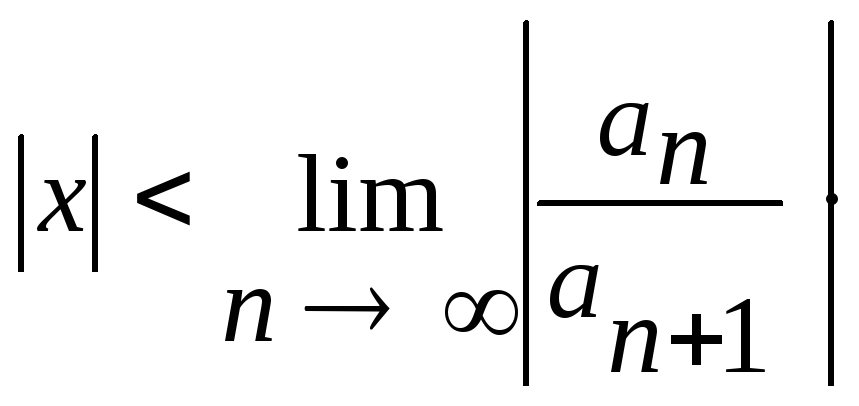, і розбігається для тих х, коли Таким чином є радіус збіжності степеневого ряду

Аналогічно скориставшись ознакою Коші, можна встановити, що: R=lim

Неважко переконатись, що коли L=lim або L= lim ,то ряд (1) є абсолютно збіжним на всій числовій осі. У цьому разі вважають R = + 00. Якщо ж L = 0, то R = 0, і степеневий ряд має лише одну точку збіжності х = 0.

Питання про збіжність ряду при х = ± R (на кінцях інтервалу збіжності) розв'язується для кожного ряду окремо. Таким чином, область збіжності степеневого ряду може відрізнятись від інтервалу (—R; R) не більше ніж двома точками х = ± R.

Рівності =називаються формуламиКошi-Адамара.

Область збiжностi степеневого ряду (1) - це одна з множин (x₀-R, x₀+R), [x₀-R, x₀+R], (x0 -R,x₀ + R] або [x₀ -R,x₀ + R).

Теор. 2 (рiвномiрна збiжн.степеневих рядiв). Нехай r Є (0,R). Тодi ряд (1)

рiвномiрнозбiжнийна[-r,r].

Доведення. Згiдно з теоремою про абсолютну збiжнiсть степеневого ряду, ряд rⁿ абсолютно збiжний, тобто ряд rⁿ збiжний. Оскiльки |a_nxⁿ| < |a_n|rⁿ при x _є [-r, r], то згiдно з ознакою Вейєрштрасса ряд (1) рiвномiрно збiжний на [-r, r].

Теор. (неперервнiсть суми степеневого ряду). Нехай f(x) = xⁿ i R - радiус

збiжностi цього ряду. Тодi функцiя f(x) неперервна на (-R, R).

Довед.. Нехай x₀ Є (-R,R). Виберемо таке r Є (0,R), що x₀ Є (-r,r) С (-R,R). Згiдно з попередньою теоремою ряд xⁿ рiвномiрно збiжний на (-r,r). Врахувавши, що всi функцiї a_nxⁿ неперервнi, одержимо, що функцiя f неперервна на (-r,r) як сума рiвномiрно збiжного ряду з неперервних функцiй. Зокрема, функцiя f неперервна в точцi x ₀.

2. Принцип максимуму для розв’язкiв рiвняння теплопровiдностi.

Рівняння вигляду називаєтья рівнянням теплопровідності

В площині розглянемо скінчену область , обмежену кривою Побудуємо циліндричну поверхню з направляючою і твірною, паралельною осі . Частину циліндричної поверхні, яка міститься між площинами i (–додатна стала), позначимо через , а через – проекцію області на площину . Область, обмежену границею , позначимо через , a .

Теорема. Нехай функція належить перетину і задовольняє в однорідне рівняння теплопровідності

. (3.1)

Тоді функція своє найбільше та найменше значення в області приймає на .

Д о в е д е н н я. Зауважимо, що функція задовольняє всі умови теореми, а її значення всюди в області є однаковим. Але це не суперечить твердженню теореми, тому що найбільше та найменше значення функції в області не більше і не менше значень цієї функції на (вони збігаються).

Доведення теореми достатньо

провести для випадку найбільшого

Рис. 41 значення. Дійсно, якщо функція в деякій точці розглядуваної області досягає найбільшого значення, то в цій точці функція досягає найменшого значення, а остання задовольняє всі умови сформульованої теореми.

Теорема. Нехай функція належить перетину

Якщо всюди в , то функція досягає свого найбільшого значення наЯкщо жвсюди в , то на функціядосягає найменшого значення.

Наслідок. Якщо два розв’язки однорідного рівняння теплопровідності задовольняють умову

і належать класу , тодля всіх

4. Задано точки A(3; −4; −2) та B(2; 5; 2). Знайти проекцiю вектора −→AB на вiсь, яка утворює з координатними осями OX, OY кути α = 60◦ , β = 120◦ , а з вiссю OZ – тупий ку