
PrikladnayaMekhanika
.pdf
111
Таблиця 3.12.
Значення коефіцієнта KF
Окружна |
Ступінь |
|
|
швидкість |
KF |
||
точність |
|||
V, м/с |
|
||
|
|
||
До 5 |
7 |
1,07 |
|
8 |
1,22 |
||
|
|||
|
9 |
1,35 |
|
5÷10 |
7 |
1,20 |
|
8 |
1,30 |
||
|
|||
10÷15 |
7 |
1,25 |
|
8 |
1,40 |
||
|
Перевірка межі міцності зубців при перевантаженні. При дії короткочасних перевантажень зубці перевіряють на пластичну деформацію або крихкий злам від максимального навантаження. За умовами завдання
максимальне навантаження Tmax .
T1
Розрахунок на контактну міцність за максимальним контактним напруженням.
Розрахунок виконуємо для колеса за формулою:
H(max) H |
|
Tmax |
H |
, |
(3.90) |
|
T |
||||||
|
|
max |
|
|||
де Н – розрахункове контактне напруження, викликуване розрахунковим контактним моментом (раніше визначено по (3.80));
[ Н]max – допустиме максимальне контактне напруження.
При термооброблені (нормалізація, поліпшення або об'ємне загартування):
|
|
H max 2,8 T , |
|
(3.91) |
|||||
де Т – межа текучості матеріалу (табл. 3.1); |
|
|
|||||||
при цементації зубців і загартуванні струмами високої частоти: |
|
||||||||
H max 40 HRC. |
|
|
|
|
|
|
|
(3.92) |
|
Розрахунок за максимальним напруженням на згин: |
|
||||||||
|
|
Fmax |
|
F |
|
Tmax |
|
, |
(3.93) |
|
|
||||||||
|
|
|
|
T1 |
F max |
|
|||
|
|
|
|
|
|
|
|
||
де F – менше зі значень напруження на згин, розрахованих за формулами |
|||||||||
(3.86) і (3.87); |
|
|
|
|
|
|
|
|
|
[ F]max – максимальне припустиме напруження на згин: |
|
||||||||
при НВ ≤ 350 |
F max 0,8 Т ; |
|
|
|
|
|
|
(3.94) |
|
при НВ ≥ 350 |
F max 0,6 B . |
|
|
|
|
|
|
(3.95) |
|

112
Розрахунок відкритої циліндричної зубчастої передачі. Враховуючи умови і характер роботи відкритих передач (недостатня захищеність від забруднення абразивними частинками і збільшений абразивний знос при поганому змащенні, великі деформації валів, що приводить до збільшення зазорів в зачепленні, зростанню динамічних навантажень, до пониження міцності зношених зубів унаслідок зменшення площі їх поперечного перетину і, як наслідок, до поломки зубів), дані передачі рекомендують розраховувати по напруженням згину. У цих передачах викришування не спостерігається, оскільки поверхневі шари зубів зношуються і віддаляються раніше, ніж з'являються втомні тріщини.
Для проектного розрахунку відкритих передач по напруженням згину визначають модуль зачеплення з виразів [1]:
для прямозубих коліс:
m |
3 3 T1 106 KF YF1 Z1 |
bm F1 , |
(3.96) |
|
для косозубих коліс: |
|
|
|
|
mn 3 |
2 T1 106 KF ZF YF1 |
Z1 bm F1 |
, |
(3.97) |
де Z1 – число зубів шестерні відкритої передачі;
bm – коефіцієнт ширини зубчатого вінця колеса щодо модуля, рекомендують призначати для відкритих передач bm 10...15;
[ F1] – допустимі напруження згину зубів шестерні, Н/мм2, визначають відповідно до (3.86);
Т1 – момент на шестерні, Н мм; KF – визначається за рис.3.17;
YF1 – дивися табл. 3.10;
ZF – коефіцієнт підвищення міцності косозубих передач по
напруженням згину: |
|
KF Y |
|
|
|
ZF |
|
, |
(3.98) |
||
|
|||||
|
|
|
|
||
де – коефіцієнт торцевого перекриття (3.83);
KF – коефіцієнт розподілу навантаження між зубцями (табл. 3.12); Y – коефіцієнт, що враховує кут нахилу зубців (3.89).
Набутого значення модуля округляють у більшу сторону до значення із стандартного ряду модулів (див. табл. 3.6).
Знаючи значення модуля, визначають геометричні розміри шестерні. Діаметр ділильний для прямозубих коліс:
d1 m z1, |
(3.99) |
|||
для косозубих: |
mn |
|
|
|
d |
z , |
(3.100) |
||
cos |
||||
1 |
1 |
|
||
|
113 |
діаметр вершин зубів: |
(3.101) |
da1 d1 2 m, |
|
діаметр западин зубів: |
(3.102) |
df1 d1 2,5 m, |
|
ширина вінця: |
|
b1 bm m 2...4 . |
(3.103) |
Точність обчислення діаметрів шестерні до 0,001 мм, значення ширини зубчатого вінця округляють до цілого числа по нормальних лінійних розмірах (див. табл. Д1). Перевірочний розрахунок такої передачі по контактним напруженням виконують відповідно до розрахунків наведених на стор.107 («Перевірочний розрахунок зубців передачі на міцність»).
3.2.2.Планетарні зубчаті передачі
Планетарними називають передачі, що мають зубчаті колеса з осями, що
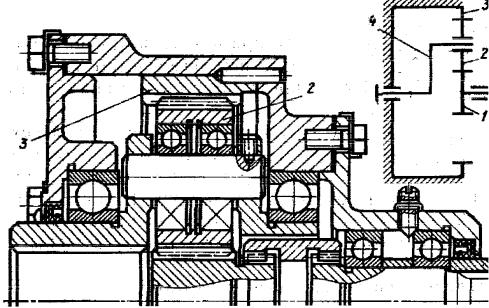
переміщуються в просторі [4-6,33]. Ці колеса рухаються подібно до планет Сонячної системи, вони обертаються навколо своїх осей і одночасно переміщаються разом з осями, здійснюючи плоский рух і називаються сателітами (лат. satellitum – супутник). Рухомі колеса котяться по центральних колесах (їх іноді називають сонячними колесами, рис. 3.18, поз.1), маючи з ними зовнішнє, а з корончатим колесом (рис. 3.18, поз.3) внутрішнє зачеплення. Осі сателітів рухомо закріплені у водилі (рис. 3.18, поз.4) і обертаються разом з ним навколо центральної осі.
Рис. 3.18. Планетарна передача: 1 – сонячне колесо; 2 – сателіти; 3 – корончате колесо; 4 – водило
Планетарні передачі мають ряд переваг перед звичайними:
великі передатні відношення при малих габаритах і масі;
можливість складання або віднімання швидкості;
легке управління і регулювання швидкості;
малий шум унаслідок замикання сил в механізмі.
114
У планетарних передачах широко застосовують внутрішнє зубчате зачеплення з кутом w=30о.
Для забезпечення складання планетарних передач необхідно дотримувати: умову співвісності (збіг геометричних центрів коліс); умову збірки (сума зубів центральних коліс кратна числу сателітів) і умову сусідства (вершини зубців сателітів не повинні стикатися один з одним).
Зубчасті колеса планетарних передач розраховуються за тими ж законами, що і колеса звичайних циліндричних передач [44].
3.2.3.Хвильовізубчатіпередачі
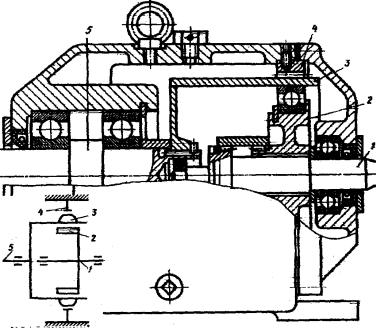
Це циліндричні передачі, де одне з коліс має гнучкий вінець. Цей гнучкий вінець деформується генератором хвиль спеціальної некруглої форми і входить у зачеплення з центральним колесом в одній, двох або декількох зонах [15] (рис.3.19).
Ідея хвилевих передач полягає в наявності декількох пар зачеплення, які ще і переміщаються по колу, за рахунок чого досягається величезне передавальне відношення (зазвичай U=60 300, відомі конструкції з U>1000). І це в одній ступені!
Принцип роботи хвильової передачі аналогічний роботі планетарної передачі з внутрішнім зачепленням і сателітом, який в процесі роботи деформується.
Така передача була запатентована американським інженером Массером в
1959 р.
Рис. 3.19. Хвильова передача: 1 – вхідний вал; 2 – генератор хвиль; 3 – гнучке зубчасте колесо; 4 – жорстке зубчасте колесо; 5 – вихідний вал
До переваг хвильових передач відносяться:
невелика маса і габарити;
велика кінематична точність;
менший мертвий хід;
115
високу віброміцність за рахунок демпфування (розсіяння енергії) коливань;
створюють менший шум;
при необхідності такі передачі дозволяють передавати рух в герметичний простір без застосування ущільнюючих сальників, що особливо цінно для авіаційної, космічної і підводної техніки, а також для машин хімічної промисловості.
До недоліків хвилевих передач відносяться:
обмежені обороти ведучого валу (щоб уникнути великих
відцентрових сил інерції некруглого генератора хвиль);
дрібні модулі зубів (1,5 – 2 мм);
практично індивідуальне, дороге, вельми трудомістке виготовлення гнучкого колеса і генератора.
Основні види поломок хвилевих передач:
руйнування підшипника генератора хвиль від навантаження в зачепленні;
проскакування генератора хвиль при великих крутних моментах, коли зуби на вході в зачеплення упираються один в одного вершинами;
поломка гнучкого колеса від тріщин втоми (особливо при U < 80);
знос зубів на кінцях;
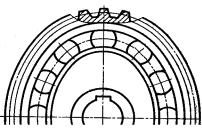
пластичні деформації бічних поверхонь зубів при перевантаженнях. Розрахунок хвилевих зубчатих передач відрізняється від розрахунку
звичайних зубчастих передач тим, що враховується деформація гнучкого вінця і генератора [14,42] (рис.3.20).
Рис. 3.20. Генератор хвиль
За критерій працездатності зазвичай приймають допустиме напруження на зминання:
зм 10Мкр / dd3 зм ; |
(3.104) |
де d – коефіцієнт ширини гнучкого вінця; d – ділильний діаметр гнучкого вінця.
3.2.4.ЗачепленняНовікова
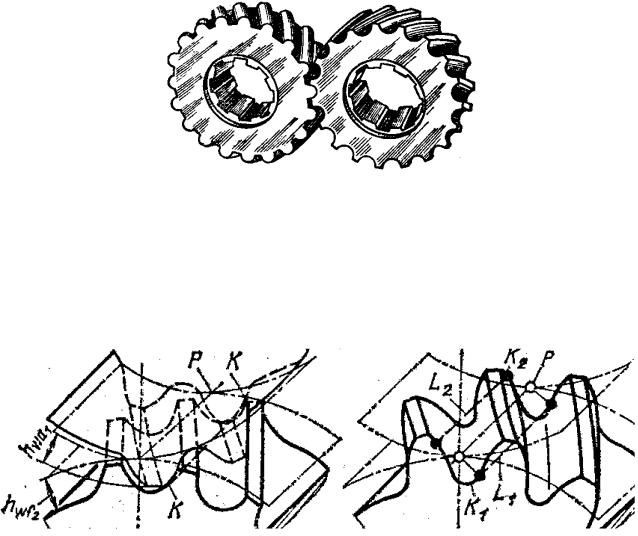
Отже, основний недолік зубчатих передач з евольвентним профілем (циліндричних, конічних, планетарних, хвильових) – високе контактне напруження в зубцях. Вони великі тому, що контактують два зуби з опуклими профілями. При цьому майданчик контакту дуже малий, а контактні
116
напруження відповідно високі. Ця обставина сильно обмежує "несучу здатність передачі", тобто не дозволяє передавати великі крутні моменти.
Вирішуючи проблеми проектування важких тихохідних машин, таких як трактори і танки, М.Л. Новіков в 1954 році розробив зачеплення, в якому опуклі зубці шестерні входять у зачеплення з увігнутими зубцями колеса (рис.3.21).
До того ж опуклий і увігнутий профілі (зазвичай круги) мають близькі по абсолютній величині радіуси кривизни. За рахунок цього виходить великий майданчик контакту, контактні напруження зменшується і з'являється можливість передавати більші приблизно в 1,4 1,8 рази крутні моменти.
Рис. 3.21. Зачеплення Новікова
На жаль, при цьому доводиться пожертвувати основною гідністю евольвентних зачеплень – коченням профілів зубів один по одному і відповідно отримати високе тертя в зубах. Проте для тихохідних машин це не так важливо.
Робочі бічні поверхні зубців мають кругловінтові поверхні, тому передачі можна називати кругловінтовими. Надалі був розроблений варіант передачі з двома лініями зачеплення. У ній зубці кожного колеса мають увігнуті ніжки і опуклі голівки.
а |
б |
Рис. 3.22. Колеса з однією (а) та двома (б) лініями зачеплення
Передачі з двома лініями зачеплення мають більшу несучу здатність, менш чутливі до зсуву осей, працюють з меншим шумом і більш технологічні. Ці передачі успішно застосовуються при малих числах зубів (Z1<10) і дають достатню жорсткість шестерні при її великій відносній ширині.
Зачеплення Новікова в редукторах застосовують замість переходу на колеса з твердими поверхнями.

117
Розрахунок передач Новікова на контактну міцність проводять на основі формули Герца–Бєляєва, враховуючи експериментально встановлений факт, що несуча здатність передач, за інших рівних умов назад пропорційна синусу кута нахилу зубів. Крім того, в розрахунку трохи збільшуються допустимі напруження.
Передачі бувають однопарні, використовуються в редукторах загального призначення і багатопарні, які отримують за рахунок збільшення осьового розміру і використовуються в прокатних станах, редукторах, турбінах і тому подібних механізмах.
3.2.5.Конічнізубчатіпередачі
Передають крутний момент між валами осі яких пересікаються (частіше всього під кутом 900). Їх зубці бувають прямими, косими, круглими і зазвичай мають евольвентний профіль (рис. 3.23).
Рис. 3.23. Конічні зубчасті передачі
І хоча, конічні колеса складніше циліндричних як по своїй геометрії, так і при виготовленні, принципи силової взаємодії, умови роботи, а отже, і методика розрахунку аналогічні циліндричним.
Тут ми розглянемо тільки відмітні особливості розрахунку конічних коліс
(рис. 3.24).
Рис. 3.24. Схема конічної передачі

118
Спочатку конструктор вибирає зовнішній окружний модуль mte, з якого розраховується вся геометрія зачеплення, зокрема, нормальний модуль в середині зуба:
|
b |
|
|
mnm mte 1 0,5 |
|
, |
(3.105) |
|
|||
|
Re |
|
|
де Re – зовнішня конусна відстань;
b– ширина зубця.
Сили в конічній передачі діють аналогічно циліндровій, проте слід
пам'ятати, що із-за перпендикулярності осей радіальна сила на шестерні аналогічна осьовій силі для колеса і навпаки, а окружна сила при переході від шестерні до колеса тільки міняє знак:
Fr1 Fa2; Fr2 Fa1; Ft1 Ft2 . (3.106)
Розрахунки на міцність конічних коліс [13] проводять аналогічно циліндричним, по тій же методиці [2]. З умови контактної витривалості визначають зовнішній ділильний діаметр dwe, з умови міцності на згин знаходять нормальний модуль в середині зуба mnm. При цьому в розрахунок
приймаються уявні еквівалентні колеса з числами зубців: |
|
|||||||||
|
Z |
е1,2 |
|
Z1,2 |
. |
(3.107) |
||||
|
|
|
||||||||
|
|
|
|
cos |
|
|||||
Діаметри: |
|
|
|
|
|
1,2 |
|
|
|
|
|
|
|
|
mte Z1,2 |
|
|
|
|||
d |
е1,2 |
|
. |
(3.108) |
||||||
|
||||||||||
|
|
|
cos |
|
||||||
|
|
|
|
|
|
1,2 |
|
|
|
|
Тут Z1, Z2 – фактичні числа зубів конічних коліс. При цьому числа Zе1,2 можуть бути дробами.
У еквівалентних циліндричних колесах [20] діаметр початкового кола і модуль відповідають середньому перетину конічного зуба, замість міжосьової відстані береться середня конусна відстань [33], а профілі еквівалентних зубів отримують розгорткою додаткового конуса на площину.
Розрахунок закритої конічної зубчатої передачі. Найбільше застосування в редукторобудуванні отримали прямозубі конічні колеса, у яких осі валів перетинаються під кутом =90 (рис. 3.25).
Проектний розрахунок. Основний габаритний розмір передачі – ділильний діаметр колеса по зовнішньому торцю. Його розраховують по формулі [1]:
|
|
|
de2 1,7 3 |
Eпр T2 KH up |
, |
(3.109) |
|
|
|
|
0,85 H 2 |
1 Kbe Kbe |
|||
|
|
|
|
|
|
||
де |
Eпр |
|
– приведений модуль |
пружності, для |
сталевих коліс |
||
E |
E |
|
2,1 105 МПа; |
|
|
|
|
пр |
сталі |
|
|
|
|
|
|
|
T2 |
– крутний момент на валу колеса, Н мм; |
|
|
|||
119
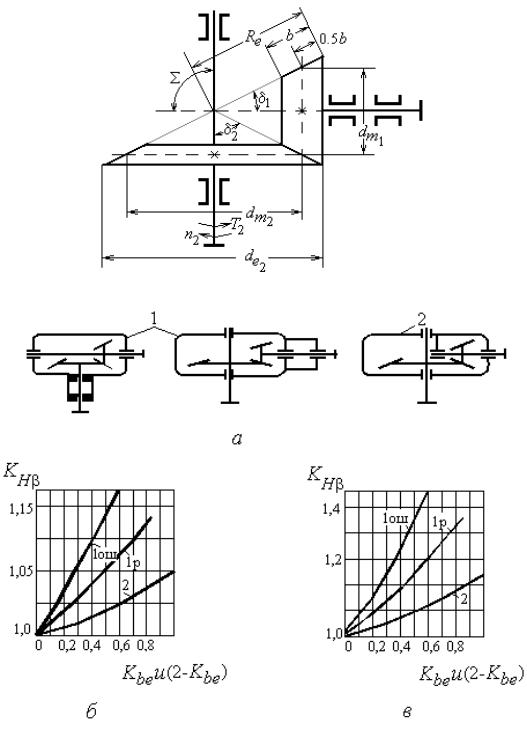
KH – коефіцієнт нерівномірності розподілу навантаження по довжині
зуба, визначають по графіках на рис. 3.26.
Kbe – коефіцієнт ширини зубчатого вінця щодо зовнішньої конусної відстані:
K |
be |
|
bw |
, |
(3.110) |
|
|||||
|
|
Re |
|
||
рекомендують приймати Kbe 0,3. Менші значення призначають для зубчатих коліс, що не приробляються, коли HВ1 і HВ2>350 HB або V>15 м/с.
Рис. 3.25. Геометричні параметри конічної передачі
Рис. 3.26. Графіки до визначення KH
120
Найбільш поширено в редукторобудуванні значення Kbe 0,285, тоді
попередній вираз для визначення ділильного діаметру по зовнішньому торцю колеса приймає вигляд:
d |
|
2,9 3 |
Eпр T2 KH up |
, |
(3.111) |
|
|
||||
|
e2 |
|
0,85 H 2 |
|
|
де up – розрахункове передавальне число конічної передачі.
Геометричний розрахунок. Визначають діаметр шестерні по зовнішньому торцю:
|
|
dl |
|
dl |
2p |
. |
(3.112) |
|
|
|
|
||||
|
|
1p |
up |
|
|||
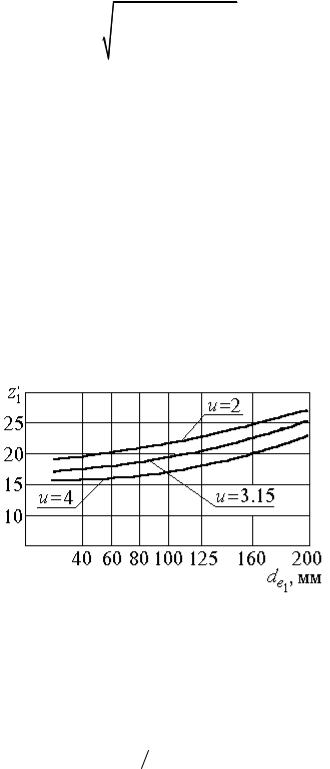
Число зубів шестерні Z1' |
призначають по рекомендаціях, представлених |
||||||
на рис. 3.27. |
|
|
|
|
|
|
|
За значенням Z1' визначають число зубів шестерні: |
|
||||||
z1 1,6z1 |
при НВ1 |
і НВ2 350 HB, |
|
||||
z1 1,3z1 |
при НВ1 |
45 HRC і НВ2 350 HB, |
|
||||
z1 z1 при НВ1 і НВ2 45 HRC.
Обчислене значення z1 округляють до цілого числа.
Рис. 3.27. Графік до визначення числа зубів шестерні Z1' |
|
Визначають число зубів колеса: |
|
z2 u z1. |
(3.113) |
Обчислене значення z2 округляють до цілого числа. Після цього |
|
необхідно уточнити: |
|
- передавальне число передачі: |
|
uф z2 z1; |
(3.114) |
- кут ділильного конуса колеса: |
|
2ф arctg uф ; |
(3.115) |
- кут ділильного конуса шестерні: |
|
1ф 90 2ф; |
(3.116) |
