PrikladnayaMekhanika

Таким чином, в межах другої ділянки брус розтягнутий і нормальна сила змінюється по лінійному закону.

Аналогічний результат виходить і при розгляді правої відсіченої частини (рис. 2.4,г):

На основі отриманих даних будується епюра нормальних сил у вигляді графіка розподілу нормальної сили по довжині бруса (рис. 2.4,д). Характерно, що скачки на епюрі обумовлені наявністю у відповідних перетинах зосереджених сил R і Р.

Епюри внутрішніх зусиль при крученні.

Крученням називається простий вид опору, при якому до бруса (валу) прикладаються зовнішні пари сил в площинах, співпадаючих з поперечним перетином валу, а в останніх виникає тільки внутрішній момент, що крутить.

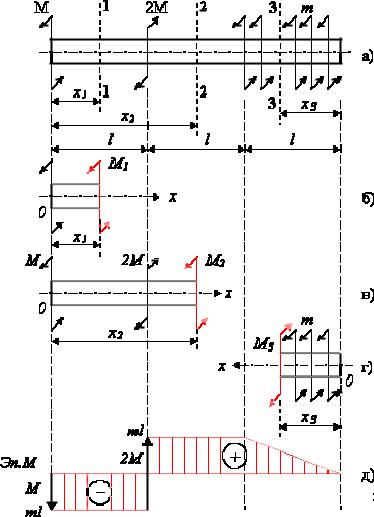
Розглянемо розрахункову схему валу, навантаженого двома зосередженими моментами М і 2М і розподіленими по довжині m (рис. 2.5).

Методика побудови епюри аналогічна тільки що розглянутій методиці при розтягуванні-стисканні.

У початкових перетинах № 1, 2 і 3 задаються позитивними значеннями внутрішніх моментів М1, що крутять, М2, М3. Нехай М=m·l.

Для першої ділянки (рис. 2.5,б):

M1 M m l const

33

Відмічені значення ординат відкладаються на епюрі внутрішніх крутних моментів (рис. 2.5,д).

2.4.Епюривнутрішніхзусильприпрямомувигині

Прямим вигином (згином) називається такий вид простого опору, коли зовнішні сили прикладені перпендикулярно подовжній осі бруса (балки) і розташовані в одній з головних площин у відповідність з конфігурацією поперечного перетину балки.

Як відомо, при прямому вигині в поперечному перетині виникають два види внутрішніх зусиль: поперечна сила і внутрішній момент, що вигинає.

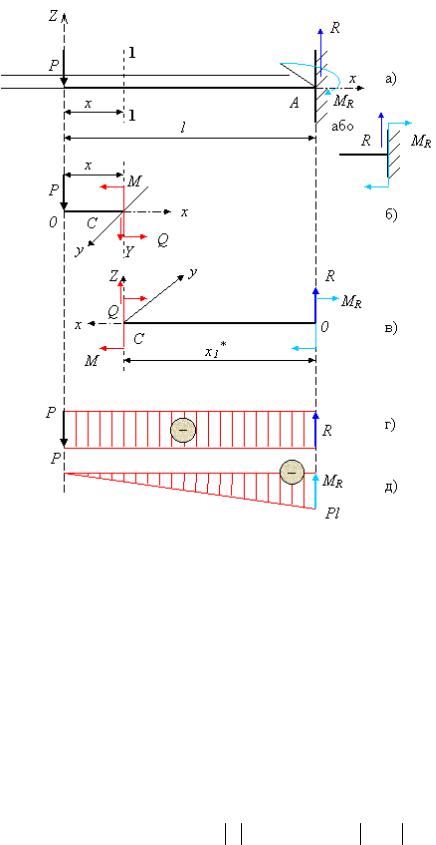
Розглянемо приклад розрахункової схеми консольної балки із зосередженою силою Р (рис. 2.6,а).

Перш за все обчислимо реакції зв'язку на базі рівнянь рівноваги:

n

MR P l

Після уявного розтину балки нормальним перетином 1–1 розглянемо рівновагу лівої відсіченої частини (рис. 2.6,б), отримаємо:

n

Таким чином, на першій ділянці поперечна сила негативна і постійна, а внутрішній згинаючий момент змінюється по лінійному закону.

Для правої відсіченої частини при розгляді її рівноваги результат аналогічний (рис. 2.6,в). А саме:

Q R P

34

Рис. 2.6. Побудова епюр поперечних зусиль та внутрішніх згинаючих моментів при прямому згині: а – розрахункова схема; б – ліва частина стрижня; в – права частина стрижня; г – епюра поперечних зусиль; д – епюра згинающих моментів

n

На підставі набутих значень будуються епюри поперечних сил (рис. 2.6,г) і внутрішніх моментів, що вигинають (рис. 2.6,д).

Як випливає з побудованих епюр Q P const, а Mmax P l в перетині

жорсткого зв'язку. Саме цей перетин і є найбільш небезпечним в даній розрахунковій схемі.

Продиференціюємо вираз внутрішнього згинаючого моменту по координаті х:

Після диференціювання внутрішнього згинаючого моменту отримали вираз для поперечної сили.

Диференціальні залежності між внутрішніми зусиллями при вигині.

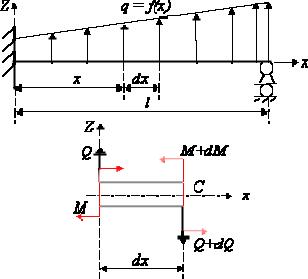
Перший характерний приклад. Розглянемо розрахункову схему балки з довільним розподіленим навантаженням q f x (рис.2.7).

Рис. 2.7. Схема згину балки

Складемо рівняння рівноваги:

n

використовується при перевірці правильності побудови епюр. Так, для розрахункової схеми консольної балки (рис.2.6) цей зв'язок дає наступні перевірочні результати:

Q 0 і М убуває від 0 до -P·l. Q const і М пропорційний х.

Розглянемо другий характерний приклад вигину двоопорної балки

(рис.2.8).

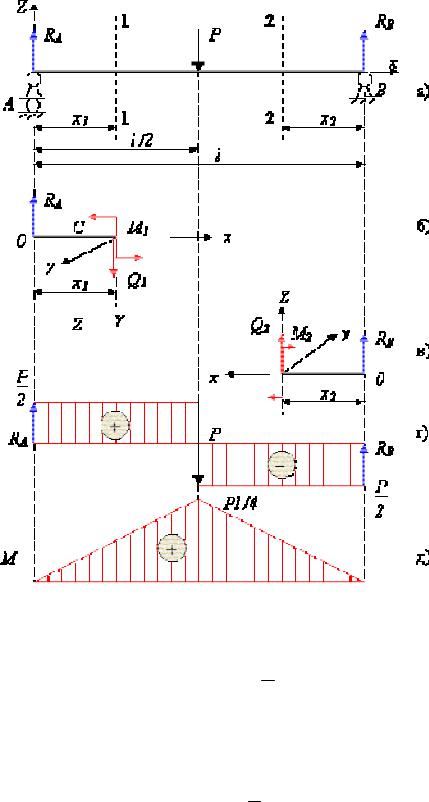
36

Рис. 2.8. Згин балки на двох опорах. Побудова епюр поперечних зусиль та внутрішніх згинаючих моментів: а – розрахункова схема; б –ліва частина стрижня; в – права частина стрижня; г – епюра поперечних зусиль (Q); д – епюра згинающих моментів (M)

Очевидно, що опорні реакції RA RB P :

2

– для першої ділянки (рис.2.8, б):

n

Piz Q1 RA 0

i 1

Q R

P

1 A 2

n

My M1 RA x1 0

i 1

M1 RA x1

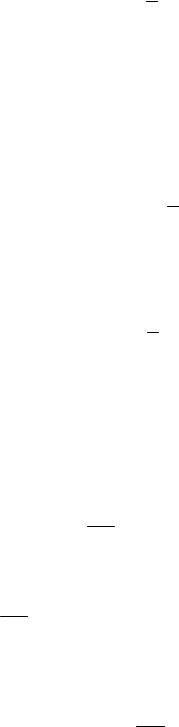
37

l 0 x1 2

M1 0 0

– для другої ділянки (рис.2.8, в):

n

Piz Q2 RB 0

i 1

P Q2 RB 2

n

My M2 RB x2 0

i 1

M2 RB x2

l 0 x2 2

M2 0 0

Епюри внутрішніх зусиль представлені відповідно на рис.2.8, г і д. На основі диференціального зв'язку Q і М, отримаємо:

для першої ділянки:

Q > 0 і М зростає від нуля до P l .

4

Q = const і M пропорційний x;

для другої ділянки:

Q < 0 і М убуває з P l до нуля.

4

Q = const і M також пропорційний х, тобто змінюється по лінійному закону.

Небезпечним в даному прикладі є перетин балки в центрі прольоту:

P l

Mmax 4

Третій характерний приклад: зв'язаний з використанням розподіленого по довжині балки навантаження (рис.2.9). Слідуючи методиці, прийнятій

перетину (рис.2.9, б) вирази для внутрішніх зусиль набувають вигляду:

n

Piz Q RA qx 0

i 1

Q RA qx

38

0 x l

Q 0 RA

Q l RA ql ql ql ql 2 2

Рис. 2.9. Балка з рівномірно розподіленим навантаженням на двох опорах. Побудова епюр поперечних зусиль та внутрішніх згинаючих моментів: а – розрахункова схема; б –ліва частина стрижня; в – епюра поперечних зусиль; г – епюра згинающих моментів

властивості функції і похідної при dM 0, внутрішній момент, що вигинає, dx

39

досягає екстремуму. Для знаходження початкової координати х0 (рис.2.9,в) у загальному випадку прирівняємо вираз поперечної сили до нуля. У результаті отримаємо:

dM

Q RA q x0 0 dx

x0 RA ql l q 2q 2

Після підстановки x l у вираз моменту, що вигинає, отримаємо:

2

q l2

Таким чином Mmax 8 .

2.5.Поняттяпронапруженняідеформації

Як зазначено вище, внутрішні сили, що діють в деякому перетині з боку відкинутої частини тіла, можна привести до головного вектора і головного моменту. Зафіксуємо точку М в даному перетині з одиничним вектором нормалі n. Біля цієї точки виділимо малий майданчик ΔF. Головний вектор внутрішніх сил, що діють на цьому майданчику, позначимо через ΔP (рис. 2.10,а). При зменшенні розмірів майданчика відповідно зменшуються головний вектор і головний момент внутрішніх сил, причому головний момент зменшується більшою мірою.

а) б)

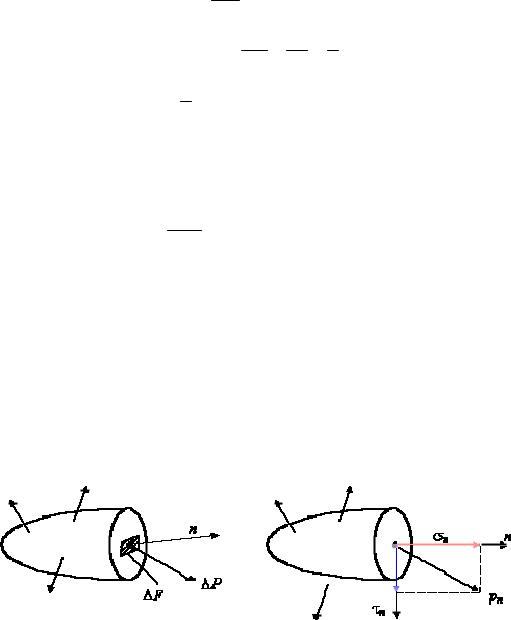
Рис. 2.10. Композиція вектора напруження: а – вектор повного напруження; б – вектори нормального та дотичного напруження

Аналогічна межа для головного моменту рівна нулю. Введений таким чином вектор pn називається вектором напруження в точці. Цей вектор залежить не тільки від зовнішніх сил, що діють на тіло, і координат даної точки, але і від орієнтації в просторі майданчика ΔF, що характеризується вектором n.

40

Сукупність всіх векторів напруги в точці М для всіляких напрямів вектора n визначає напружений стан в цій точці.

У загальному випадку напрям вектора напруги pn не співпадає з напрямом вектора нормалі n. Проекція вектора pn на напрям вектора n називається нормальним напруженням n , а проекція на площину, що проходить через точку М і ортогональна вектору, – дотичним напруженням

n (рис. 2.10,б).

Розмірність напруження дорівнює відношенню розмірності сили до розмірності площі. У міжнародній системі одиниць СІ напруження вимірюються в паскалях: 1 Па=1 Н/м2.

При дії зовнішніх сил разом з виникненням напруження відбувається зміна об'єму тіла і його форми, тобто тіло деформується. При цьому розрізняють початковий (недеформоване) і кінцевий (деформоване) стани тіла.

Віднесемо недеформоване тіло до декартової системи координат Oxyz (рис. 2.11). Положення деякої точки М в цій системі координат визначається радіус-вектором r(х, у, z). У деформованому стані точка М займе нове положення М', що характеризується радіус-вектором r' (х, у, z). Вектор u=r'-r називається вектором переміщень точки М. Проекції вектора u на координатні осі визначають компоненти вектора переміщень u(х, у, z), v(х, у, z), w(х, у, z), рівні різниці декартових координат точки тіла після і до деформації.

Рис. 2.11. Композиція вектора переміщення

Переміщення, при якому взаємне розташування точок тіла не міняється, не супроводжується деформаціями. В цьому випадку говорять, що тіло переміщається як жорстке ціле (лінійне переміщення в просторі або поворот щодо деякої крапки). З іншого боку, деформація, пов'язана із зміною форми тіла і його об'єму, неможлива без переміщення його точок.

Деформації тіла характеризуються зміною взаємного розташування точок тіла до і після деформації. Розглянемо, наприклад, точку М і близьку до неї точку N, відстань між якими в недеформованому стані уздовж напряму вектора s позначимо через ΔS (рис. 2.12). У деформованому стані точки М і N