
PrikladnayaMekhanika
.pdf
61
Для того, щоб сформулювати передумови теорії розтягування (стиснення) призматичного стрижня, звернемося до експерименту. Уявимо собі стрижень, виготовлений з якого-небудь податливого матеріалу (наприклад, гуми), на бічну поверхню якого нанесена система подовжніх і поперечних рисок (рис.2.23,а). Ця ортогональна система рисок залишається такою і після додатку розтягуючого навантаження (рис. 2.23,б). Оскільки поперечні риски є слідами поперечних перетинів на поверхні стрижня і залишаються прямими і перпендикулярними до осі стрижня то це свідчить про виконання гіпотези плоских перетинів (Бернуллі). З урахуванням гіпотези про відсутність поперечної взаємодії подовжніх волокон приходимо до висновку, що деформація розтягування стрижня зводиться до одноосного розтягування його подовжніх волокон, і в поперечному перетині стрижня виникає лише нормальні напруження (рис. 2.24), індекс у яких опускаємо. Ортогональність подовжніх і поперечних рисок свідчить також про відсутність зрушень, а, отже, і пов'язані з ними дотичні напруження в поперечних і подовжніх перетинах стрижня.
Рис. 2.23. Модель розтягнутого стрижня |
Рис. 2.24. Зв'язок напруження і |
|
подовження |
Тоді подовжня сила NZ рівна сумі проекції внутрішніх сил, що діють в даному поперечному перетині площею F (рис. 2.24) очевидно буде дорівнювати:
NZ dF, |
(2.110) |
F |
|
Це співвідношення є рівнянням рівноваги статики, що зв'язує подовжню силу NZ, і нормальні напруження , які в загальному випадку є функцією координат х і у і тому не може бути знайдено з лише одного рівняння статики. Таким чином, завдання визначення напруження навіть в найпростішому випадку деформації стрижня (розтягуванні або стисненні) виявляється статично невизначним.
Необхідне для вирішення цього завдання додаткове рівняння витікає з гіпотези плоских перетинів. Оскільки поперечні перетини стрижня, залишаючись плоскими і перпендикулярними до осі стрижня, в процесі деформації лише поступально переміщаються уздовж осі стрижня (що приводить до однакового подовження всіх подовжніх волокон), то приходимо
62
до рівняння =const, з якого зважаючи на однозначність зв'язку і (для лінійно-пружного матеріалу це – закон Гуку) витікає, що:
const . (2.111)
Вирішуючи спільно рівняння отримаємо, що:
NZ F |
(2.112) |
||
або |
|
||
|
NZ |
. |
(2.113) |
|
|||
|
F |
|
|
Таким чином, при розтягуванні (стисненні) призматичного стрижня нормальні напруження рівномірно розподілені по поперечному перетину, а дотичні напруження в перетинах відсутні, що є наслідком гіпотези плоских перетинів. Вказане, не дивлячись на, здавалося б, очевидність і простоту, є фундаментальним результатом, справедливим, строго кажучи, лише для призматичного стрижня. Проте в інженерній практиці його використовують і для наближеної оцінки нормального напруження в стрижнях змінного перетину. При цьому, щоб погрішність формули була невелика, необхідно, щоб площа поперечного перетину стрижня змінювалася достатньо плавно уздовж його осі.
Умова міцності при розтягуванні (стисненні) призматичного стрижня для стрижня з пластичного матеріалу (тобто матеріалу, що однаково працює на розтягування і стиснення) матиме вигляд:
|
NZ |
, |
(2.114) |
|
|||
|
F |
|
|
де [ ] – допустимі напруження.
Напруження в умові (2.114) підставляється по модулю, оскільки знак в цьому випадку ролі не грає. Для стрижнів з крихких матеріалів, що неоднаково чинять опір розтягуванню і стисненню, знак напруги має принципове значення, і умову міцності доводиться формулювати окремо для розтягування і стиснення:
|
P |
|
|
|
NZ |
|
|
P |
|
||
|
|
F |
|
||||||||
|
|
|
|
|
|
|
, |
(2.115) |
|||
|
|
|
|
|
|
NZ |
|
||||
|
|
|
|
|
|
|
|||||
|
C |
|
|
|
|
|
C |
|
|||
|
|
|
|||||||||
|
|
|
|
|
|||||||
|
|
|
F |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
де Р і С – напруження розтягування і стиснення; [ Р] і [ С] – що відповідають їм допустимі напруження.
У практиці інженерних розрахунків, виходячи з умови міцності, вирішуються три основні завдання механіки матеріалів конструкцій. У застосуванні до випадку розтягування (стиснення) призматичного стрижня ці завдання формулюються таким чином.
Перевірка міцності (перевірочний розрахунок). Цей розрахунок проводиться, якщо навантаження (у нашому випадку її представляє NZ), перетин стрижня F і його матеріал [ ] задані. Необхідно переконатися, що виконується умова міцності – (2.114).

63
Перевірочний розрахунок полягає в тому, що визначається фактичний коефіцієнт запасу міцності n і порівнюється з нормативним коефіцієнтом запасу
[n]:
n |
* |
|
F |
n , |
(2.116) |
|
|
||||
|
|
NZ |
|
||
де * – граничне (або небезпечне) напруження, тобто напруження, що викликає відмову елементу конструкції (нагадаємо, що, наприклад, для стрижня з пластичного матеріалу це межа текучості Т або умовна межа текучості 0,2).
Підбір перетину (проектний розрахунок). У цьому розрахунку по заданому навантаженню (NZ) визначаються розміри поперечного перетину стрижня (F) із заданого матеріалу ([ ] дано). Мінімального значення F набудемо, якщо в умові міцності (2.114) прийняти знак рівності:
F |
NZ |
, |
(2.117) |
|
Визначення допустимого навантаження тобто максимального значення навантаження, яке допускає даний елемент конструкції (F і [ ] дані) при виконанні умови міцності (2.114):
N F. |
(2.118) |
Поняття про концентрацію напруження, принцип Сен-Венана. Навіть для призматичного стрижня рівномірний розподіл напруги по поперечному перетину не завжди має місце. Так, відхилення від рівномірного розподілу напруження спостерігаються поблизу перетинів, що містять вирізи, виточки, отвори, тріщини, в місцях різкої зміни поперечного перетину, а також в місцях зосередження сил і т.і. Нерівномірний розподіл напруження у вказаних місцях є наслідком викривлення площин поперечних перетинів або їх депланації.
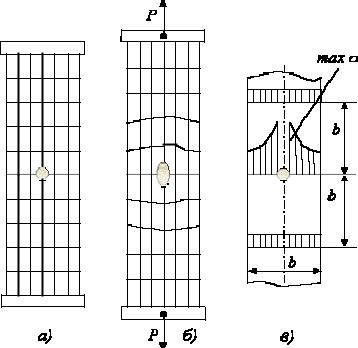
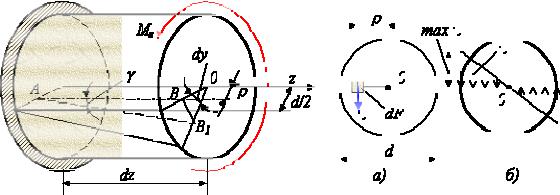
Пояснимо це явище на прикладі розтягнення смуги з податливого матеріалу з круговим отвором, на поверхні якої нанесені подовжні і поперечні ризики (рис. 2.25,а). У зоні отвору має місце депланація поперечних перетинів, викликана нерівномірним розтягуванням подовжніх волокон (рис. 2.25,б). При цьому найбільші подовження і відповідно напруження max отримують волокна біля отвору. Таке місцеве збільшення напруження біля вирізів, виточок, отворів і т. п., а також в місцях додатку зосереджених сил, називається концентрацією напруження, а джерела концентрації напруження (вирізи, виточки, отвори і т.п.) отримали назву концентраторів напруження.
Розглянутими методами механіки деформованого тіла, що спираються на гіпотезу плоских перетинів, завдання про розподіл напруження в зонах концентрації напруження не вирішуються. Такі завдання вирішуються методами теорії пружності або досліджуються експериментально. При цьому для практичних розрахунків вводиться так званий теоретичний коефіцієнт концентрації напруження К, що є відношенням максимального max і номінального НОМ напруження:
|
|
|
|
|
|
64 |
|
K |
|
max |
, |
(2.119) |
|
|
||||||
|
|
|
ном |
|
||
|
|
|
|
|
||
де НОМ – номінальні напруження, які визначається без урахування концентрації напруження.
Рис. 2.25. Концентрація напружень: а – вихідний стан; б – деформований стан; в – епюри напруження
У приведеному прикладі розтягування смуги з отвором:
|
ном |
|
NZ |
, |
(2.120) |
|
|||||
|
|
F |
|
||
|
|
|
nt |
|
|
де Fnt – площа поперечного перетину смуги, зменшена за рахунок отвору
("нетто").
Таким чином, К грає роль поправочного коефіцієнту.
Проте, як показали експерименти і точні вирішення завдань теорії пружності, місцеві відхилення від рівномірного розподілу напруження, викликані концентрацією напруження, швидко затухають у міру видалення від перетину з концентратором, і на відстанях порядку ширини перетину розподіл напруження можна рахувати практично рівномірним (рис. 2.25,в). Відмічена властивість є окремим випадком широко використовуваного практично у всіх розділах механіки деформованого твердого тіла (у тому числі і теорії пружності) принципу Сен-Венана.
Визначення деформацій і переміщень. Визначимо пружні деформації стрижня припускаючи, що зміна його довжини при розтягуванні Δl, зване
абсолютною подовжньою деформацією або подовженням, мало в порівнянні з його первинною довжиною l (Δl<<l). Тоді відносна подовжня деформація буде рівна:
|
|
|
65 |
|
l |
, |
(2.121) |
|
|||
|
l |
|
|
Враховуючи, що згідно закону Гуку для одноосного розтягування (стиснення):
|
|
, |
(2.122) |
|
E
де Е – модуль подовжньої пружності матеріалу стрижня, а нормальна напруження визначається по формулі:
|
NZ |
, |
(2.123) |
||
|
|||||
|
|
F |
|
||
(у нашому випадку NZ=P), для абсолютної деформації отримуємо: |
|
||||
l |
NZ |
, |
(2.124) |
||
|
|||||
|
E F |
|
|||
Твір EF прийнято називати жорсткістю поперечного перетину стрижня при розтягуванні (стисненні), оскільки подовження зворотно пропорційно EF.
Рис. 2.26. Моделі продольної та поперечної деформації
Як показують дослідження, при розтягуванні стрижня розміри його поперечного перетину зменшуються (див. рис.2.26), а при стисненні - збільшуються. Це явище отримала назва ефекту Пуассона.
По аналогії з подовжньою деформацією зміна розмірів поперечного перетину (на рис. 2.26 Δb<0) називатимемо абсолютною поперечною
деформацією, а b – відносною поперечною деформацією. Відносні b
подовжня і поперечна деформації, такі, що мають протилежні знаки, зв'язані між собою коефіцієнтом , що є константою матеріалу і названий коефіцієнтом поперечної деформації або коефіцієнтом Пуассона:
|
(2.125) |
, |
Як відомо, для ізотропного матеріалу 0 0,5.
Формула (2.124) для подовження стрижня Δl застосовна тільки у разі, коли по довжині стрижня ні жорсткість поперечного перетину, ні подовжня сила не змінюються (EF=const, NZ=const). Подовження стрижня із ступінчастою зміною EF і NZ (рис. 2.27) може бути визначено як сума подовжень ступенів, у яких EF і NZ постійні:
n |
NZk lk |
n |
k lk |
|
|
|
l |
|
, |
(2.126) |
|||
E F |
|
|||||
k 1 |
k 1 |
E |
|
|||
|
k |
|
|
|
|
|

66
(індекс k у модуля подовжньої пружності означає, що ділянки стрижня можуть бути виготовлені з різних матеріалів). У разі, коли NZ і EF міняються по довжині стрижня l безперервно і їх можна вважати постійними лише в межах ступенів довжиною dz, узагальнюючи цю формулу, отримуємо:
l
l NZdz . (2.127) 0 EF
Рис. 2.27. Ступінчастий брус
З пружними подовжніми деформаціями стрижня при розтягуванні (стисненні) зв'язані подовжні переміщення його перетинів. На рис. 2.28 приведено три випадки визначення таких переміщень, звідки видно, що переміщення поперечних перетинів чисельно рівні подовженням заштрихованих частин стрижня:
переміщення вільного торцевого перетину 1-1 при нерухомому другому торцевому перетині (рис. 2.28,а) чисельно дорівнює подовженню стрижня;
переміщення проміжного перетину 2-2 (рис. 2.28,б) чисельно рівно подовженню частини стрижня, ув’язненому між даним перетином і перетином нерухомим;
взаємне переміщення перетинів 3-3 і 4-4 (рис. 2.28,в) чисельно рівно подовженню частини стрижня, ув’язненому між цими перетинами.
Рис. 2.28. Моделі переміщення
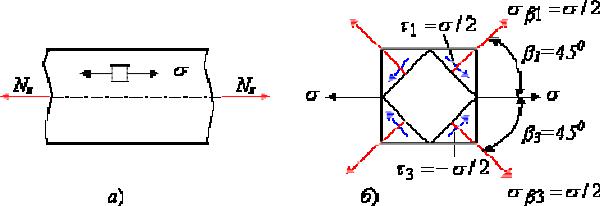
Напружений стан при розтягуванні (стисненні). Напружений стан при розтягуванні стрижня є одноосним (рис. 2.29,а). Оскільки на поперечних і подовжніх майданчиках дотична напруження не виникає, то ці майданчики є
67
головними. Причому у разі розтягування 1= >0, 2= 3=0, а у разі стиснення,
1= 2=0, а 3= <0.
Рис. 2.29. Напруженний стан: а – вихідний елемент; б – компонента напруження
Напруження на майданчиках, нахилених до осі стрижня під кутом , визначаються по формулах для спрощеного плоского напруженого стану:
cos2 , 0,5 sin2 . (2.128)
Майданчики з екстремальними дотичними напругою 13 (рис. 2.29,б), як відомо, нахилені по відношенню до початкових під кутами =±45 (слідує і з формули для ) і рівні 13= /2.
Саме з дією екстремальних зв'язується поява на бічній поверхні зразка з маловуглецевої сталі, що випробовується на розтягування, ліній ковзання, орієнтованих під кутом =±45 до осі зразка. На майданчиках з екстремальними
діють і нормальні напруження, які дорівнюють 13= /2.
2.10.Напруження і деформації при крученні призматичних стрижнівкруговогопоперечногоперетину
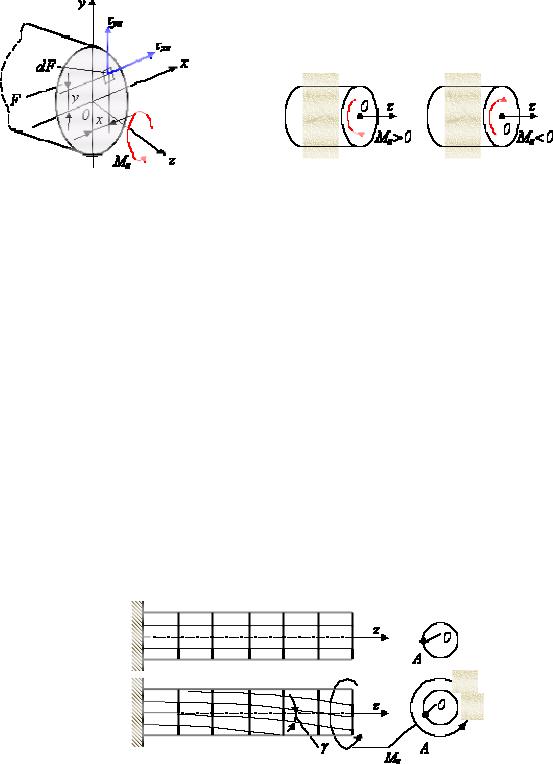
Крученням називається такий вид деформації, при якому в поперечному перетині стрижня виникає лише один силовий чинник – крутний момент МZ. Крутний момент за визначенням дорівнює сумі моментів внутрішніх сил щодо подовжньої осі стрижня Oz. Нормальні сили, паралельні осі Oz, внеску до крутного моменту не вносять. З силами, лежачими в площині поперечного перетину стрижня (інтенсивності цих сил – дотичні напруження xz і yz) МZ зв'язано рівняннями рівноваги статики (рис. 2.30):
MZ yxx xzy dF. |
(2.129) |
F |
|
Умовимося вважати МZ позитивним, якщо з боку відкинутої частини стрижня його видно направленим проти годинникової стрілки (див. рис. 2.31). Це правило проілюстроване на рис. 2.30 і у вказаному співвідношенні, де крутний момент МZ прийнято позитивним. Чисельно крутний момент рівний сумі моментів зовнішніх сил, прикладених до відсіченої частини стрижня, щодо осі Оz.
68
Рис. 2.30. Зв'язок крутного момента з |
Рис. 2.31. Схеми позитивного і негативного |
дотичними напруженнями |
крутного моменту |
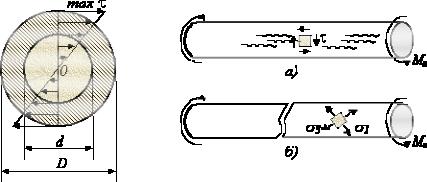
Розглянемо кручення призматичних стрижнів кругового поперечного перетину. Дослідження деформацій пружного стрижня з нанесеною на його поверхні ортогональною сіткою рисок (рис. 2.32) дозволяє сформулювати наступні передумови теорії кручення цього стрижня:
1.Поперечні перетини залишаються плоскими (виконується гіпотеза Бернуллі);
2.Відстані між поперечними перетинами не змінюються, отже Z=0;
3.Контури поперечних перетинів і їх радіуси не деформуються. Це означає, що поперечні перетини поводяться як жорсткі кругові пластинки, що повертаються при деформації щодо осі стрижня Оz. Звідси витікає, що будь-які
деформації в площині пластинки рівні нулю, у тому числі і X= Y=0;
4. Матеріал стрижня підкоряється закону Гуку. Враховуючи, що X= Y=Z=0, з узагальненого закону Гуку у формі отримуємо X= Y= Z=0. Це означає, що в поперечних перетинах, стрижня виникає лише дотичні напруження , а унаслідок закону парності дотичного напруження, рівні ним напруження діють і в зв'язаних подовжніх перетинах. Отже напружений стан стрижня – чистий зсув.
Рис. 2.32. Схеми кручення: а – вихідне; б – деформований стан
Виведемо формулу для дотичного напруження при крученні призматичного стрижня кругового поперечного перетину. Як видно, поворот правого торцевого перетину щодо нерухомого лівого на кут (назвемо його кутом закручування стрижня) викликає поворот подовжніх волокон на кут (кут зрушення), оскільки на величину змінюються кути ортогональної сітки подовжніх і поперечних рисок моделі.
69
Двома суміжними перетинами виріжемо елемент стрижня довжиною dz і, оскільки нас цікавлять деформації елементу, лівий перетин його вважатимемо нерухомим (рис. 2.33). При повороті правого перетину на кут d відповідно до гіпотези про недеформованість радіусів, правий кінець волокна АВ (віддалений від осі елементу на величину полярного радіусу ) переміщатиметься по дузі BB1, викликаючи поворот волокна на кут зсуву:
|
BB1 |
|
d |
. |
(2.130) |
AB |
|
||||
|
|
dz |
|
||
Звернемо увагу на те, що відповідно до рис. 2.33 і рис. 2.34,а зрушення і пов'язане з ним дотичне напруження перпендикулярні радіусу . Визначимо, скориставшись законом Гуку для чистого зсуву:
G G |
d |
. |
(2.131) |
|
|||
|
dz |
|
|
де d /dz – погонний кут закручування стрижня, який залишається поки невідомим. Для його знаходження звернемося до умови статики, записавши його в зручнішій для даного випадку формі (рис. 2.34,а):
MZ dF. |
(2.132) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.33. Розрахункова модель визначення |
Рис. 2.34. Розподілення дотичних напружень |
дотичних напружень |
при крученні: а – ортогональність и ; б – |
|
епюра дотичних напружень |
Підставляючи (2.131) у (2.132) і враховуючи, що |
|
2 dF JP , |
(2.133) |
F |
|
де Jp – полярний момент інерції поперечного перетину (для круга з діаметром d Jp= d4/32), отримуємо:
d |
|
MZ |
. |
(2.134) |
|
|
|||
dz |
G JP |
|
||
70
Рис. 2.35. Розподіл напруження для |
Рис. 2.36. Розподілення вихідних дотичних і головних |
кольцевого перетину |
напружень: а – руйнування деревини; б – руйнування |
|
металу |
Підставляючи вираз (2.134) у (2.131), отримуємо формулу для дотичного напруження при крученні призматичного стрижня кругового поперечного перетину:
|
MZ |
. |
(2.135) |
|
|||
|
JP |
|
|
Як видно з (2.135), зсув і дотичні напруження пропорційні відстані від осі стрижня. Звернемо увагу на структурні аналогії формул для нормального напруження чистого вигину і дотичного напруження кручення.
Мірою деформації стрижня при крученні є погонний кут закручування стрижня, визначуваний по (2.134). Оскільки величина G·JP стоїть в знаменнику формули і при заданому навантаженні (МZ через неї виражається) d /dz тим менше, чим більше G·JP, останню називають жорсткістю поперечного перетину при крученні.
Користуючись (2.134) для визначення кута закручування елементу довжиною dz:
d |
MZ |
|
dz, |
(2.136) |
|||
G JP |
|||||||
|
|
|
|
||||
знайдемо повний кут закручування стрижня довжиною l: |
|
||||||
l |
MZ |
|
dz, |
(2.137) |
|||
|
|
||||||
|
0 G JP |
|
|||||
У випадку, якщо по довжині стрижня МZ і G·JP постійні, отримуємо:
|
MZ l |
, |
|
(2.138) |
|
|
|
||||
|
G JP |
|
|
||
коли ці величини сталі на різних ділянках стрижня, то: |
|
||||
n |
MZk lk |
|
|
||
k 1 |
|
, |
(2.139) |
||
G JP k |
|||||
Відзначимо, що отримані формули по структурі аналогічні формулам для деформацій при розтягуванні стрижня.
