127838-229237

УДК 531+539.19+536(075.8) ББК 22.2

Э45

А в то р ы :

А.А. Маскевич, В.Ф. Аскирка, Г.Т. Василюк, В.Е. Воронич, Е.Е. Трофименко (БНТУ).

Р е ц е н з е н т ы :

кафедра физики БГУИР (зав. кафедрой – Квасов Н.Т., доктор физико-математических наук, профессор);

Хило П.А., зав. кафедрой физики ГГТУ им. П.О. Сухого, доктор физико-математических наук, профессор.

Электричество и магнетизм. Волновая оптика : учеб. пособие / Э45 А.А. Маскевич [и др.]. – Гродно : ГрГУ, 2008. – 375 с.

ISBN 978-985-515-041-2

Учебное пособие включает в себя разделы «Электродинамика» и «Волновые процессы» курса «Физика». В начале каждого раздела излагаются основные понятия, определения, законы и формулы, снабженные необходимыми пояснениями. Подробно разобраны примеры решения типовых задач, приведены более 750 задач различного уровня сложности для самостоятельного решения, справочный материал в виде приложений. Адресовано студентам инженерно-технических специальностей вузов.

ВВЕДЕНИЕ

Курс «Физика» занимает особое место в программе подготовки специалистов инженерно-технического профиля. Он служит фундаментом самостоятельного освоения новых идей, новых тенденций в стремительно развивающемся мире науки, техники и технологий. Умение решать задачи является лучшей оценкой глубины знания учебного материала, а навыки моделирования при изучении физики помогут будущему специалисту при разрешении реальных технических и производственных проблем.

Целью настоящего учебного пособия является оказание помощи студентам инженерно-технических специальностей при изучении курса «Физика» в систематизации знаний по данной дисциплине и при решении задач контрольных и индивидуальных заданий.

Данная книга является продолжением учебного пособия В.Ф. Аскирки, В.В. Войны, А.М. Колодинского, А.А. Маскевича «Механика, молекулярная физика и термодинамика»*, она адресована студентам как дневных, так вечерних и заочных форм обучения, включает в себя разделы «Электродинамика» и «Волновые процессы». В начале каждого из них приведены основные понятия, определения, законы и формулы, снабженные необходимыми пояснениями. Обе теоретические части являются фактически кратким конспектом по разделам «Электричество и магнетизм», «Оптика», «Механические и электромагнитные колебания и волны» курса «Физика». Далее следуют подробно разобранные примеры решения типовых задач, порядок расположения которых соответствует порядку изложения материала в теоретических частях. При решении каждой задачи даются ссылки на законы и формулы в теоретической части, что позволяет «видеть» логику рассуждений. Более 750 задач, предложенных для самостоятельного решения, можно использовать при организации самостоятельной рабо-

* Механика, молекулярная физика и термодинамика: учеб. пособие / В.Ф. Аскирка [и др.]. – Гродно: ГрГУ, 2005. – 184 с.

3

ты студентов, при проведении контрольных работ и коллоквиумов. Все задачи распределены по темам, соответствующим главам теоретической части. Для составления различных вариантов заданий преподаватель имеет возможность комбинировать задачи из разных глав на свое усмотрение с учетом сложившихся традиций преподавания физики студентам различных специальностей. Заканчивается пособие справочным материалом, необходимым для решения задач, представленным в виде приложений. Для студен- тов-заочников приведены правила по выполнению и требования к оформлению контрольных работ.

Авторы надеются, что данное пособие будет востребовано для обеспечения учебного процесса по курсу «Физика» в учебных заведениях, обеспечивающих получение высшего образования по инженерно-техническим специальностям, в частности в организации самостоятельной (в том числе и контролируемой) работы студентов.

Авторы будут признательны всем за замечания и предложения, касающиеся содержания настоящего пособия.

4

Раздел 1. ЭЛЕКТРОДИНАМИКА

1. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ. ЗАКОН КУЛОНА

Электростатика – раздел физики, изучающий электрические поля, созданные неподвижными электрическими зарядами, а также взаимодействия между такими зарядами.

Электрический заряд – это характеристика тел или частиц, определяющая их способность к электромагнитному взаимодействию.

Наряду с электрически нейтральными частицами (например, фотонами), существуют элементарные частицы – носители эле-

ментарного электрического заряда двух типов: положительного

(протоны) и отрицательного (электроны). Электроны и протоны входят в состав всех атомов и молекул, что и обусловливает наличие у макроскопических тел равных по величине отрицательных и положительных зарядов.

Экспериментально доказано, что электрический заряд q любого макроскопического тела состоит из целого числа элементарных зарядов обоих знаков: ± ne , где e =1,60 ×10−19 Кл – элементарный заряд, n – целое число. Электрически нейтральное тело содержит одинаковое число протонов и электронов.

Первоначально электрически нейтральное тело можно зарядить путем трения тел друг о друга; соприкосновением с заряженным телом; разделением электрических зарядов

ская индукция).

Удельный заряд частицы – отношение заряда частицы к ее массе ( q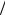m ) – является основной характеристикой элементарных

частиц и определяет значение заряда, приходящееся на единицу массы. Так как массы электрона и протона соответственно равны me = 9,11×10−31 кг и mp =1,67 ×10−27 кг, то их удельные заряды

составляют eme =1,76 ×1011 Кл/кг, emp = 9,6 ×107 Кл/кг.

В случае взаимодействия заряженных тел (частиц) одно-

именные заряды отталкиваются, разноименные – притягиваются.

5

Величина заряда не зависит от выбора инерциальной системы отсчета – заряд релятивистски инвариантен.

Система, не обменивающаяся зарядами с внешними телами,

называется замкнутой (изолированной).

Закон сохранения электрического заряда: алгебраическая сумма электрических зарядов в замкнутой системе не изменяется при любых процессах, происходящих в этой системе:

Закон взаимодействия неподвижных электрических зарядов экспериментально установлен и сформулирован Ш. Кулоном для

точечных электрических зарядов – таких заряженных тел, раз-

меры которых малы по сравнению с расстоянием между ними.

Закон Кулона: модуль силы взаимодействия F двух не- подвижных точечных зарядов, находящихся в вакууме, прямо про-

где e0 – электрическая постоянная ( e0 = 8,85 ×10−12 Ф/м). Коэффициент пропорциональности в законе Кулона часто за-

писывают в виде k = 4pe1 0 = 9,0 ×109 Н×м2/Кл2.

Закон Кулона в виде (1.2) справедлив также для заряженных макроскопических тел, имеющих сферическую форму. В этом случае расстояние r определяется между центрами сферических тел.

В векторной форме закон Кулона представляется в виде:

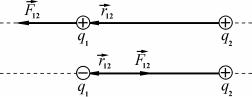
Сила F12 направлена по прямой (рис. 1.1), соединяющей

взаимодействующие точечные заряды (центры сферических зарядов), и называется силой Кулона (кулоновской силой). Направление кулоновских сил определяется знаками взаимодействующих зарядов.

Рис. 1.1

Силы электростатического взаимодействия удовлетворяют третьему закону Ньютона: F12 = −F21 , то есть силы электростати-

ческого взаимодействия двух зарядов равны по модулю и противоположны по направлению.

Если заряды q1 и q2 взаимодействуют в изотропной и однородной среде с диэлектрической проницаемостью ε , то сила Ку-

Электрическое поле – векторное поле, определяющее силовое воздействие на заряженные частицы, не зависящее от их скоростей.

Электрическое поле создается как неподвижными, так и движущимися зарядами и является одной из компонент единого электромагнитного поля.

Поле, связанное с неподвижными электрическими зарядами,

называется электростатическим.

Напряженность электрического поля – векторная величина,

равная отношению силы F , действующей на неподвижный положительный пробный заряд q0 , помещенный в данную точку поля, к величине этого заряда:

7

[E]=1Н/Кл =1 В/м.

Пробный заряд q0 – точечный заряд, который не должен существенно возмущать исследуемое поле.

Как видно из определения, вектор E равен силе, действующей на единичный положительный неподвижный заряд.

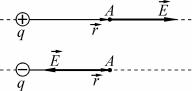
Напряженность поля, создаваемого точечным зарядом, в

некоторой точке A (рис. 1.2) находится из выражения:

поля, или в скалярной форме:

Рис. 1.2

Графически электростатическое поле отображается с помо-

щью линий напряженности (силовых линий) – линий, касатель-

ные к которым в каждой точке совпадают с направлением вектора

напряженности поля E в этой точке (рис. 1.3). Силовые линии проводят таким образом, чтобы их густота была пропорциональна модулю вектора напряженности.

Электростатическое поле однородно, когда вектор напря-

женности поля в любой точке пространства постоянен по модулю и направлению. В этом случае силовые линии представляют собой

параллельные прямые.

8

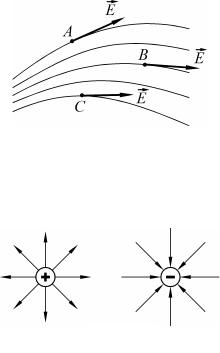
Рис. 1.3

Если поле создается точечными зарядами, то линии напря-

женности – радиально исходящие из заряда (для положительно-

го) или входящие (для отрицательного) прямые (рис. 1.4).

Рис. 1.4

Если электростатическое поле создается несколькими точечными неподвижными зарядами, то величина суммарного поля оп-

ределяется принципом суперпозиции: напряженность поля,

создаваемого всеми зарядами, равна геометрической сумме на- пряженностей, создаваемых каждым зарядом в отдельности не- зависимо от других, то есть:

2. ТЕОРЕМА ГАУССА ДЛЯ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ В ВАКУУМЕ

Элементарный поток вектора напряженности через беско-

нечно малую площадку dS равен скалярному произведению вектора напряженности E на вектор dS :

9

между векторами E и n (рис. 1.5).

Рис. 1.5

Поток вектора напряженности допускает графическую интерпретацию, основанную на понятии силовых линий. Так как число силовых линий электрического поля, проходящих через единичную площадку, перпендикулярную направлению вектора напря-

женности пропорционально E , то поток вектора напряженности поля через площадку пропорционален числу силовых линий, пересекающих ее поверхность.

Поток вектора напряженности электростатического поля че-

рез произвольную поверхность определяется интегралом:

Теорема Гаусса для электростатического поля в вакууме:

поток вектора напряженности электростатического поля в ва- кууме через произвольную замкнутую поверхность равен алгеб- раической сумме зарядов, заключенных внутри этой поверхности, деленной на e0 :

* Здесь и далее символом «×» обозначено скалярное произведение векторов.

10