
127838-229237
.pdf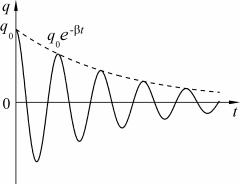
|
Рис. 1.36 |
|
||
Время релаксации τ |
– время, за которое амплитуда колеба- |
|||
ний уменьшается в e раз. |
Коэффициент затухания β связан с |
|||
временем релаксации соотношением: |
|
|||
τ = |
1 |
. |
(13.10) |
|
|
||||
|
|
β |
|
|
Логарифмический декремент затухания λ определяется как натуральный логарифм отношения двух значений амплитуд, взя-
тых через интервал времени, равный периоду колебаний T : |
|
|||||
|
|
a(t) |
|
|||
|
λ = ln |
|
|
|
= βT , |
(13.11) |
|
a(t + T ) |
|||||
где a – |
амплитуда соответствующей физической величины ( q , |
|||||
U , I ). |
Ne – количество колебаний за время релаксации, то |
|||||
Если |
||||||
логарифмический декремент затухания можно выразить иначе: |
||||||
|
λ = |
1 |
. |
(13.12) |
||
|
|
|||||
|
|
|
Ne |
|
||
Добротность колебательного контура характеризует «эф- |
||||||
фективность» рассеяния энергии контура при наличии в нем активного сопротивления. Эта величина определяется из соотношения:
Q = |
π |
= πNe . |
(13.13) |
|
λ |
||||
|
|
|
||
|
|
51 |
|

При малом затухании добротность контура равна отношению энергии, запасенной в контуре в произвольный момент времени t , к убыли этой энергии за период, умноженному на 2π :
W (t) |
|
Q = 2p W (t)-W (t + T ) . |
(13.14) |
Вынужденные колебания – незатухающие колебания, возникающие в R, L, C -цепи под действием внешнего периодически
изменяющегося напряжения: |
|
U = U 0 cos wt , |
(13.15) |
где U 0 – амплитудное значение напряжения, |
ω – циклическая |
частота напряжения. |
|
Сила тока I в такой цепи также изменяется по синусоидальному закону, но сдвинута по фазе относительно фазы колебаний
напряжения на величину, равную ϕ : |
|
I = I0 cos(wt + j) , |
(13.16) |
где I0 – амплитудное значение силы тока. |
|
Закон Ома для переменного тока: сила тока при устано-
вившихся вынужденных колебаниях в цепи, содержащей последо- вательно включенные R , L и C , определяется выражением:
|
|
|
I0 |
= |
|
|
|
|
|
|
U 0 |
|
|
|
|
, |
(13.17) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
2 |
æ |
|
1 ö2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
R |
|
+ çwL |
- |
|
÷ |
|
|
|
||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
è |
|
wC ø |
|
||||
|
|
2 |
æ |
|
1 |
|
ö |
2 |
|
|
|
|
|
|
|
||
где Z = |
R |
|
+ çwL |
- |
|
|
|
|
÷ – полное сопротивление цепи пе- |
||||||||
|
wC |
||||||||||||||||
|
|
|
è |
|
ø |
|
|
|
|
|
|
|
|
||||
ременного тока (или импеданс), R – активное сопротивление,
X L = wL – реактивное индуктивное сопротивление, |
X C = |
1 |
– |
|||
wC |
||||||
реактивное емкостное сопротивление. |
|
|
||||
|
|
|
||||
Величина X L - X C = wL - |
1 |
– реактивное |
сопротив- |
|||
wC
ление.
52

Для расчета цепей синусоидального тока широкое примене-
ние получил символический, или комплексный, метод, в кото-
ром токи и напряжения заменяют их комплексными изображениями или символами.
Метод основан на том, что в цепях синусоидального переменного тока от уравнений, составленных на основе правил Кирхгофа для мгновенных значений токов и напряжений и являющихся дифференциальными уравнениями, можно перейти к алгебраическим уравнениям, составленным относительно комплексных символов тока и напряжения. При этом мгновенное значение тока i
заменяют комплексным символом I& , который в экспоненциальной форме комплексного числа имеет вид I& = I0 e jϕ , где ϕ – фаза тока
i относительно фазы, выбранной за нулевую. Мгновенное значение напряжения на активном сопротивлении R = Ri заменяют комплексом RI& , по фазе совпадающим с током I& . Мгновенное значение напряжения на индуктивности uL = L(di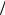 dt) заменяют
dt) заменяют
комплексом I&jwL , опережающим ток на 90o ; мгновенное значе-
|
|
1 |
|
æ |
- j ö |
|
ние напряжения на емкости uC |
= |
|
òidt – комплексом |
I&ç |
|
÷ , |
C |
|
|||||
|
|
|
è wC ø |
|||
отстающим от тока на 90o ; мгновенное значение напряжения u –
& |
|
|
|
|
|
|
|
комплексом U , который в экспоненциальной форме комплексного |
|||||||
& |
|
jϕ |
|
|
|
|
|
=U0 e . |
|
|
|
|
|||
числа имеет вид U |
|
|
|
|
|||
Закон Ома в символической форме для R, L, C -цепи пере- |
|||||||
менного тока определяется выражением: |
|
||||||
|
|
|
& |
|
|
|
|
|
I& = |
|
U |
|
|
, |
(13.18) |
|
R + jwL - |
j |
|
||||
|
|
wC |
|
||||
|
|
|
|
|
|||
где U& – комплексный символ напряжения, I& – комплексный символ тока, R – комплексный символ активного сопротивления R (содержит только действительную часть), jωL – комплексный
символ индуктивного сопротивления, w-Cj – комплексный символ емкостного сопротивления.
53
Выражение |
|
= R + jωL − |
j |
называется |
полным ком- |
|
Z |
||||||
ωC |
||||||
|
|
|
|
R, L,C -цепи пе- |
||
плексным сопротивлением последовательной |
||||||
ременного тока.
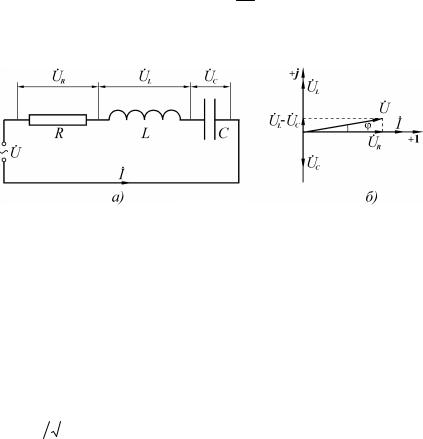
Так как токи и напряжения на различных участках электрической цепи синусоидального тока, как правило, по фазе не совпадают, то наглядное представление о фазовом расположении различных векторов дает векторная диаграмма напряжений и токов. Для этого изображают две взаимно-перпендикулярные оси: по оси абсцисс откладывают действительную часть комплексного значения тока или напряжения (обозначают + 1), а по оси ординат –
мнимую (обозначают + j , где j = 
 −1 ). Для простейшей схемы
−1 ). Для простейшей схемы
(рис. 1.37 а) приведен пример векторной диаграммы на рисунке
1.37 б.
Рис. 1.37
Сдвиг фаз ϕ между током и напряжением в цепи синусои-
дального тока определяется соотношением: |
|
|||||
|
ωL − |
1 |
|
|
|
|
tgϕ = |
ωC |
. |
(13.19) |
|||
|
||||||
R |
|
|||||
|
|
|
|
|
||
Активная мощность в цепи переменного тока – среднее значение мгновенной мощности p за период T :
|
|
|
1 |
T |
U |
m |
I |
m |
|
|
|
|
P = |
|
òuidt = |
|
|
cos ϕ = UI cos ϕ , |
(13.20) |
||
|
T |
|
2 |
|
||||||
где I |
|
|
0 |
|
|
|
|
|||
– действующее |
|
(эффективное) значение |
силы тока |
|||||||
( I = I0 |
|
), U – действующее (эффективное) значение напряже- |
||||||||
2 |
||||||||||
|
|
|
|
|
|
|
|
54 |
|
|

ния (U = U 0 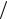

 2 ), ϕ – сдвиг фаз между током и напряжением в цепи.
2 ), ϕ – сдвиг фаз между током и напряжением в цепи.
Действующим значением силы переменного тока называ-
ется сила такого постоянного тока, при которой в данной цепи выделяется такая же мощность, как и при переменном токе. Анало-
гично определяется действующее значение напряжения.
Реактивная мощность в цепи переменного тока находится из соотношения:
Q = IU sin ϕ , |
(13.21) |
где I – действующее значение силы тока, U – действующее значение напряжения, ϕ – сдвиг фаз между током и напряжением.
Реактивная мощность измеряется в вольт-амперах |
реактивных |
(ВАр). |
|
Полная мощность в цепи переменного тока определяется |
|
выражением: |
|
S = IU , |
(13.22) |
где I и U – действующие значения силы тока и напряжения соответственно. Полная мощность переменного тока измеряется в вольт-амперах (ВА).
Полная, активная и реактивная мощности связаны соотно-
шением: |
|
|
|
|
|
|
|
|
|
S = |
|
|
P2 + Q2 . |
(13.23) |
|||
В комплексной форме записи: |
|
|
|
|
||||
~ |
& & |
* |
; |
|
|
|
|
(13.24) |
полная мощность S |
= UI |
|
|
|
|
|
||
|
|
|
&&* |
] ; |
|
|
(13.25) |
|
активная мощность P = Re[UI |
|
|
||||||
|
|
|
&&* |
] , |
(13.26) |
|||
реактивная мощность Q = Im[UI |
||||||||
где I&* – сопряженный комплекс тока, Re[U&I&* ] и Im[U&I&* ] – дейст-
вительная и мнимая части выражения для полной мощности соответственно (подробнее в главе данного раздела «Примеры решения задач»).
55

Между частотой ν и циклической частотой ω |
имеется |
соотношение: |
|
ω = 2πν . |
(13.27) |
Первое уравнение Максвелла в интегральной форме связы-
вает циркуляцию вектора напряженности электрического поля E по произвольному замкнутому контуру L и производную по времени от магнитного потока Φ через произвольную поверхность
S , ограниченную данным контуром L : |
|
||||||||||
|
r |
r |
|
d |
r |
r |
|
dF |
|
|
|
ò |
E × dl |
= - |
ò B × dS |
= - |
. |
(13.28) |
|||||
|
|
||||||||||
L |
|
|
|
dt S |
|
|
dt |
|
|||
Уравнение (13.28) представляет собой обобщение закона электромагнитной индукции Фарадея (10.1), оно показывает, что изменяющееся во времени магнитное поле порождает вихревое
электрическое поле. При этом под E понимается напряженность суммарного электрического поля, которое складывается из электростатического поля, создаваемого неподвижными зарядами, и вихревого поля, обусловленного изменением во времени магнитного поля. Циркуляция же вектора напряженности электростатического поля всегда равна нулю (смотри выражение (3.3)).
Второе уравнение Максвелла в интегральной форме уста-
навливает связь между циркуляцией вектора напряженности маг-
нитного поля H по произвольному замкнутому контуру L и силой полного тока, охватываемого этим контуром, или, иначе говоря, пересекающего поверхность S , ограниченную этим контуром:
|
|
r æ r |
|
r |
|
|
|
|
|
r |
|
¶D ö |
r |
|
|||
ò |
|
ç |
j |
+ |
|
÷ |
× dS . |
(13.29) |
H × dl = òç |
¶t |
÷ |
||||||
L |
|
S è |
|
|
ø |
|
|
|
Уравнение (13.29) является обобщением теоремы о циркуля-
ции вектора H (11.6) с учетом гипотезы Максвелла: изменяю-
щееся во времени электрическое поле подобно току проводимо- сти (то есть току, связанному с движением электрических заря- дов в проводящей среде) порождает в окружающем пространст-
ве магнитное поле. Максвелл назвал переменное электрическое поле током смещения, а частную производную по времени от
56

вектора электрического смещения ¶¶Dt , размерность которой сов-
падает с размерностью плотности тока, – плотностью тока сме-
щения.
Сумму токов проводимости и тока смещения называют пол-
ным током. Плотность полного тока равна rjполн = rj + ¶¶Dt . Тогда
можно сказать, что вихревое магнитное поле создается полным током, то есть током проводимости (при движении электрических зарядов) и током смещения (при изменении во времени электрического поля).
Третье уравнение Максвелла в интегральной форме представляет собой теорему Гаусса для вектора D : поток вектора
электрического смещения D через произвольную замкнутую по- верхность S равен стороннему заряду q , расположенному внут-
ри этой поверхности:
ò D × dS = òrdV , |
(13.30) |
|
S |
V |
|
где ρ – объемная плотность сторонних зарядов.
Уравнение (13.30) показывает, что источниками электрического поля служат электрические заряды. По существу это уравнение эквивалентно закону Кулона и принципу суперпозиции электрических полей.
Четвертое уравнение Максвелла в интегральной форме
представляет собой теорему Гаусса для вектора |
B : поток век- |
тора магнитной индукции B через произвольную замкнутую по- |
|
верхность S всегда равен нулю: |
|
ò B × dS = 0 . |
(13.31) |
S |
|
Уравнение (13.31) отражает тот факт, что в природе не обнаружены магнитные заряды, и силовые линии магнитного поля являются замкнутыми.
Различие в знаках правых частей первого и второго уравнений Максвелла свидетельствует о том, что силовые линии вихревого
57
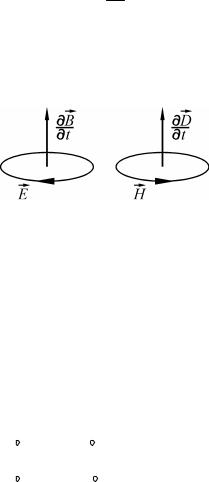
электрического поля, вызванного изменением во времени магнит-
ного поля, образуют с вектором ¶¶Bt левовинтовую систему, а ли-
нии напряженности магнитного поля, созданного изменением
электрического поля, образуют с вектором ¶D правовинтовую
¶t
систему (рис. 1.38).
Рис. 1.38
Из уравнений Максвелла видно, что переменное магнитное поле всегда связано с индуцируемым им переменным электрическим полем. И наоборот: переменное электрическое поле всегда связано с порождаемым им переменным магнитным полем. Следовательно, электрическое и магнитное поля неразрывно связаны друг с другом – они образуют единое электромагнитное поле. Из уравнений Максвелла также следует, что переменное электромагнитное поле способно существовать самостоятельно – без электрических зарядов и токов.
Для стационарных полей ( E = const и B = const ) уравнения Максвелла распадаются на две группы независимых уравнений:
ìò |
r |
r |
= 0, |
ò |
r |
r |
= 0, |
E |
× dl |
D |
× dS |
||||
ïL |
r |
r |
|
S |
r |
r |
(13.32) |
í |
= 0, |
|
|||||
ïò |
H × dl |
ò B × dS |
= 0. |
||||
îL |
|
|
|
S |
|
|
|
В этом случае источниками электрического поля являются только электрические заряды, а источниками магнитного – только токи проводимости. Стационарные электрические и магнитные поля независимы друг от друга, что позволяет изучать их по отдельности.
58
С помощью теоремы Стокса и теоремы Гаусса можно пред-
ставить систему уравнений Максвелла в дифференциальной форме (они устанавливают связь между величинами, которые характеризуют поле в каждой точке пространства):
ì |
r |
|
r |
|
r |
|
||
= - |
¶B , |
= r, |
||||||
ïrot E |
div D |
|||||||
ï |
|
|
¶t |
|
r |
|
(13.33) |
|
í |
r |
|
|
r |
||||
ï |
r |
+ |
¶D |
|
||||
ïrot H = j |
|
¶t |
, div B = 0. |
|||||
î |
|
|
|
|
|
|
||
Первая пара уравнений этой системы свидетельствует о том, что источниками электрического поля являются электрические заряды и переменное во времени магнитное поле. Вторая пара уравнений утверждает, что магнитное поле возбуждается движущимися зарядами (электрическими токами) и переменными электрическими полями.
При заданном распределении плотности зарядов и токов решение системы уравнений Максвелла в дифференциальной форме позволяет полностью определить напряженность электрического
E и индукцию магнитного B полей. Для этого уравнения Максвелла дополняют соотношениями, которые связывают D и j с
E , а также H с B , называемыми материальными уравнениями.
В случае изотропных сред, не содержащих сегнетоэлектриков и
ферромагнетиков, эти уравнения имеют вид |
|
|
r |
|
|
D = e0 eE , B = m0mH , j |
= gE |
(13.34) |
(смотри выражения (4.6), (5.16) и (11.5)).
Уравнения Максвелла являются основными законами электродинамики. Эти уравнения не выводятся, а постулируются на основе обобщения экспериментальных данных. Правильность уравнений Максвелла подтверждена совпадением многочисленных следствий этих уравнений с экспериментом.
59
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 1. Два одинаковых маленьких шарика массой 0,10 г каждый подвешены на непроводящих нитях длиной 1,0 м к одной точке. После того, как шарикам были сообщены одинаковые заряды, они разошлись на расстояние 9,0 см. Определить заряды шариков. Диэлектрическую проницаемость воздуха принять равной единице.
Дано:
m = 0,10 г =1,0 ×10−4 кг, l = 1,0 м,
r = 9,0 см = 0,090 м, ε =1,0 .
Найти: q .
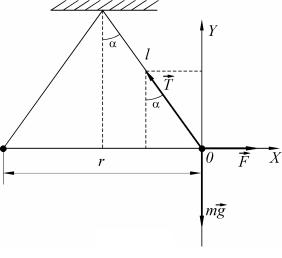
Решение. После сообщения одинаковых электрических зарядов шарики будут взаимодействовать между собой. Таким образом, на каждый заряженный шарик действуют сила тяжести mg ,
сила натяжения нити T и кулоновская сила отталкивания F
(рис. 1.39).
Рис. 1.39
60
