
127838-229237
.pdf
Каждый из шариков находится в одинаковых условиях, поэтому достаточно рассмотреть равновесие одного из них. Условие
равновесия имеет вид: |
|
r |
(1) |
T + mg + F = 0 . |
|
В проекциях на оси OX и OY получим систему: |
|
ìF - T sin a = 0, |
|
í |
|
îT cos a - mg = 0, |
|
или |
|
ìT sin a = F, |
(2) |
í |
|
îT cos a = mg. |
|
Разделив первое равенство на второе, получим значение тангенса угла отклонения шарика от положения равновесия:
tg a = |
F |
. |
|
|
|
(3) |
|||||
|
|
|
|
||||||||
|
|
|
|
mg |
|
|
|
||||
Так как угол α мал, то tg a » sin a = |
r / 2 |
= |
r |
, поэтому, с учетом |
|||||||
l |
2l |
||||||||||
|
|
|
|
|
|
|
|
|
|||
(3), получим: |
|
|
|
||||||||
|
r |
= |
F |
. |
|
|
(4) |
||||
|
|
|
|
|
|||||||
|
2l |
mg |
|
|
|
||||||
Сила электростатического взаимодействия двух точечных зарядов, находящихся в однородной изотропной среде, определяется законом Кулона [1.4]*:
F = |
1 |
|
q2 |
, |
4pe0 |
|
er2 |
||
|
|
|
тогда выражение (4) запишется в виде:
r |
= |
1 |
|
q |
2 |
, |
2l |
4pe0 |
|
|
|
||
|
|
er 2 mg |
||||
откуда окончательно находится величина искомого заряда:
q = r |
|
2pe0 emgr |
|
. |
|
l |
|||||
|
|
|
|
* В квадратных скобках даны ссылки на формулы из теоретической части. В частности, [1.4] – ссылка на 4-ю формулу 1-й главы (с. 7).
61

Подставляя числовые значения величин, получим:
q = 0,090 |
|
2×3,14×8,85×10−12 ×1,0×1,0×10−4 ×9,81×0,090 |
|
= 6,3×10−9 Кл. |
|
1,0 |
|||||
|
|
|
|
Ответ: 6,3 нКл.
Пример 2. Определить силу взаимодействия точечного заряда 5,0 нКл с тонким стержнем, равномерно заряженным с линейной плотностью 2,0 мкКл/м. Точечный заряд находится на расстоянии 10 см от стержня. Углы, образованные стержнем и прямыми, проходящими через точечный заряд и его концы, равны соответствен-
но 30o и 135o (рис. 1.40).
Дано:
τ = 2,0 мкКл/м = 2,0 ×10−6 Кл/м, r0 =10 см = 0,10 м
q0 = 5,0 нКл = 5,0 ×10−9 Кл,
a1 = 30o ,
a2 =135o .
Найти: F .
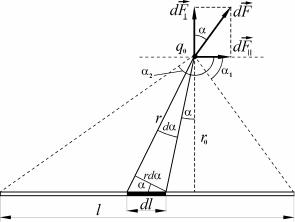
Решение. Так как размерами стержня по сравнению с расстоянием от стержня до точечного заряда пренебречь нельзя, то заряд, находящийся на стержне, не является точечным. Следовательно, воспользоваться законом Кулона в виде [1.2] непосредственно нельзя.
Однако, если выделить на стержне бесконечно малый участок длиной dl (масштаб на рис. 1.40 не соблюден), то находящийся на
нем заряд, равный |
|
dq = τdl , |
(1) |
можно рассматривать как точечный. Сила взаимодействия зарядов q0 и dq , находящихся в вакууме, по закону Кулона [1.2] будет иметь вид:
62
dF = |
1 |
|
q0 dq |
, |
4πε0 |
|
r 2 |
или с учетом выражения (1):
dF = |
1 |
|
q0 τdl |
, |
(2) |
4πε0 |
|
r 2 |
где r – расстояние от выделенного на заряженном стрежне элементарного заряда до заряда q0 .
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.40 |
Из рисунка 1.40 следует ряд геометрических соотношений |
||||||||||||
между величинами: |
|
|||||||||||
r = |
|
|
r0 |
, |
|
|
|
|
|
(3) |
||
cos α |
|
|
|
|
|
|
||||||
dl = |
|
rdα |
|
|
, |
|
|
|
(4) |
|||
cos α |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||
После подстановки соотношений (3) и (4) в выражение (2), |
||||||||||||
получим: |
1 |
|
|
|
|
|
q0 |
τ |
|
|
||
dF = |
|
|
|
|
|
dα. |
(5) |
|||||
4πε |
0 |
|
|
r |
|
|||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
0 |
|
|
|
||
Выражение (5) определяет только модуль элементарной силы dF , которая является векторной величиной. Поэтому вектор dF необ-
63

ходимо разложить на две составляющие: dF , перпендикулярную стержню, и dF|| , параллельную ему.
Из рисунка 1.40 очевидны соотношения:
dF = dF cos α, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6) |
|||||||||||||||
dF|| |
= dF sin α. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(7) |
||||||||||||||
Подставляя значение dF из выражения (5) в соотношения (6) |
||||||||||||||||||||||||||||||
и (7), получим: |
|
|
|
|
q0 τ cos α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
dF = |
|
|
1 |
|
|
|
|
|
|
dα , |
|
|
|
|
|
|
|
|
|
|
(8) |
|||||||||
|
4πε0 |
|
|
|
r0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
dF|| |
= |
|
|
1 |
|
|
|
q0 τsin α |
|
dα . |
|
|
|
|
|
|
|
|
|
|
(9) |
|||||||||
4πε0 |
|
|
|
|
|
r0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Проинтегрировав выражения (8) и (9) в пределах от α1 |
до α2 , |
|||||||||||||||||||||||||||||
получим выражения для нахождения составляющих сил F и F|| : |
||||||||||||||||||||||||||||||
|
|
α |
2 |
1 |
|
|
|
|
|
|
q0 τcos α |
|
|
q0 τ |
|
|
α2 |
|
q0 τ |
|
|
α2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
F = ò |
|
|
|
|
|
|
|
|
|
|
dα = |
|
|
|
ò cos αdα = |
|
|
sin α |
= |
|||||||||||
4πε |
|
|
|
|
|
r |
|
|
4πε |
r |
|
4πε |
r |
|||||||||||||||||
|
|
α1 |
|
|
|
0 |
0 |
|
|
|
|
|
|
0 0 |
|
α1 |
|
|
0 0 |
|
|
α1 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
= |
|
q0 τ |
|
(sin α2 − sin α1 ). |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
4πε0 r0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Аналогично находится величина второй составляющей: |
|
|
|
|||||||||||||||||||||||||||
|
|
α2 |
|
1 |
|
|
|
|
|
q0 τsin α |
|
|
|
|
q0 τ |
|
|
α2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
F|| = ò |
|
|
|
|
|
|
|
|
|
|
dα = − |
|
|
|
cos α |
= |
|
|
|
|
|
|||||||||
|
4πε |
|
|
|
|
|
|
r |
|
4πε |
r |
|
|
|
|
|
|
|||||||||||||
|
|
α1 |
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
0 0 |
|
α1 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
= |
|
q0 τ |
|
(cos α1 − cos α2 ). |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
4πε0 r0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Таким образом, модуль результирующей силы, действующей на заряд q0 , определяется по теореме Пифагора. С учетом тригонометрических соотношений получим:
|
|
|
|
|
|
q0 τ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
F = |
|
F 2 |
+ F 2 |
= |
|
|
|
(sin α |
2 |
− sin α |
1 |
)2 + (cos α |
1 |
− cos α |
2 |
)2 |
= |
||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|| |
|
|
4πε0 r0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= |
|
q0 τ |
|
2sin |
α2 |
− α1 |
|
= |
|
q0 τ |
|
sin |
α2 |
− α1 |
. |
|
|
|
|
(10) |
|||||||||
4πε |
|
r |
|
2 |
|
2πε |
|
r |
|
|
|
|
|
|
|||||||||||||||
|
0 |
|
|
|
|
|
|
0 |
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
Подставляя числовые значения величин в (10), получим:
64
F = |
|
5,0×10−9 ×2,0 ×10−6 |
sin |
135o - 30o |
=14,3×10−3 Н. |
|
2 |
×3,14×8,85×10−12 ×0,10 |
2 |
||||
|
|
|
Ответ: F = 14,3 мН.
Пример 3. Два точечных заряда + 4,5 ×10−7 Кл и - 9,0 ×10−7 Кл находятся в керосине на расстоянии 15 см друг от друга. Определить напряженность и потенциал электростатического поля в точке, расположенной на расстоянии 25 см от положительного и 20 см от отрицательного зарядов.
Дано:
q1 = +4,5 ×10−7 Кл, q2 = -9,0 ×10−7 Кл, a = 15 см = 0,15 м, r1 = 25 см = 0,25 м,
r2 = 20 см = 0,20 м, ε = 2,0 .
Найти: E , ϕ .
Решение. Неподвижные электрические заряды в пространстве вокруг себя создают электростатическое поле. Точечные заряды создают вокруг себя центрально-симметричные поля, напряженность и потенциал в некоторой точке которых определяются из соотношений [1.7], [3.6]:
E = |
1 |
|
|
q0 |
|
, |
(1) |
||
|
4pe0 |
|
er 2 |
||||||
|
|
|
|
|
|||||
j = |
1 |
|
q0 |
|
, |
|
(2) |
||
4pe0 |
|
er |
|
||||||
|
|
|
|
|
|||||
где q0 – заряд, создающий поле, r – расстояние от точечного за-
ряда до рассматриваемой точки пространства, ε – диэлектрическая проницаемость среды (числовое значение берется из таблиц).
65
В случае, если поле в данной точке создается несколькими зарядами, то суммарная напряженность определяется из принципа суперпозиции (для поля двух зарядов) [1.8]:
E = E1 + E2 , |
(3) |
где E1 и E2 – напряженности, создаваемые зарядами q1 и q2 со-
ответственно.
Потенциал точки поля определяется алгебраической суммой потенциалов, создаваемых отдельными зарядами [3.8]:
ϕ = ϕ1 + ϕ2 . |
(4) |
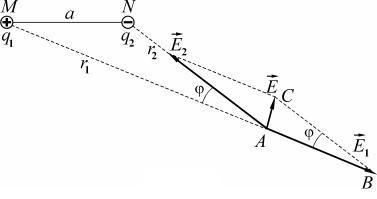
Пусть заданные заряды q1 и q2 |
расположены в точках M и |
N (рис. 1.41). В точку A , положение которой определяется расстояниями r1 и r2 от соответствующих зарядов, поместим положительный пробный заряд и определим направления векторов напряженности E1 и E2 (одноименные заряды отталкиваются, разноименные – притягиваются). По правилу параллелограмма стро-
им результирующий вектор E , |
модуль которого можно опреде- |
||||
лить из треугольника |
ABC по теореме косинусов: |
||||
E 2 = E 2 |
+ E 2 − 2E E |
2 |
cos ϕ . |
(5) |
|
1 |
2 |
1 |
|
|
|
Рис. 1.41
На основании (1) модули напряженности поля точечных зарядов (знак был учтен при выборе направлений векторов) будут иметь вид:
66

E = |
|
|
1 |
|
|
|
|
q1 |
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
4pe |
|
|
|
er 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
1 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
E |
2 |
= |
|
|
1 |
|
|
|
|
q2 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(7) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
4pe |
0 |
|
|
er 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Для нахождения косинуса угла ϕ в (5) воспользуемся теоре- |
||||||||||||||||||||||||||||||||||||
мой косинусов применительно к треугольнику ANM : |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
r |
2 |
+ r 2 |
- a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
cos j = |
|
1 |
|
2 |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
(8) |
||||||||||||
|
|
|
|
|
|
2r1r2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
С учетом выражений (6) – (8) выражение (5) примет оконча- |
||||||||||||||||||||||||||||||||||||
тельный вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
q2 |
|
|
q |
2 |
|
|
q1 |
|
|
|
q2 |
|
(r12 + r22 - a |
2 ) |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
E = |
|
|
|
|
|
|
|
|
|
1 |
|
|
+ |
|
2 |
- |
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||
4pee |
0 |
|
|
|
|
r 4 |
|
r |
4 |
|
|
|
|
|
|
|
r 3r 3 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|||||||||
Подставляя числовые значения, находим:
E = 7,78 ×10−4 В/м.
Потенциалы поля зарядов на основании (2) будут иметь вид:
|
j1 |
= |
|
|
1 |
|
|
|
q1 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(9) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
4pe0 er1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
j2 |
|
= |
|
|
1 |
|
|
|
q2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
(10) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
4pe0 er2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
На основании соотношения (4) с учетом (9) и (10) запишем: |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
æ |
|
|
|
|
|
|
|
|
|
q2 |
ö |
|
|
|
|
|
|
|
|||||
|
j = |
|
|
|
|
|
ç q1 |
+ |
÷ |
, |
|
|
|
|
|
|
|||||||||||||||||
|
4pee |
0 |
|
ç |
|
|
r |
|
|
r |
|
÷ |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
è |
1 |
|
|
|
|
|
2 |
ø |
|
|
|
|
|
|
|
|||||||||
или с учетом того, что заряд q2 отрицательный: |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
æ |
|
|
q1 |
|
|
|
|
q |
|
|
|
|
ö |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
j = |
|
|
|
|
|
|
ç |
|
|
|
|
- |
|
2 |
|
|
÷ . |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
4pee |
|
|
|
|
r |
|
|
r |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
0 |
|
ç |
|
|
|
|
|
|
|
|
|
÷ |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
è |
1 |
|
|
|
|
|
2 |
|
|
ø |
|
|
|
|
|
|||||||||
Подставляя числовые значения, найдем: |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
4,5 ×10−7 |
|
9,0 ×10−7 |
ö |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
÷ |
|
j = |
|
|
|
|
|
× 2,0 |
×8,85 ×10 |
−12 ç |
0,25 |
- |
0,20 |
÷ |
= -12145 В. |
||||||||||||||||||||
4 × 3,14 |
|
|
|
|
è |
|
ø |
|
|||||||||||||||||||||||||
Ответ: E = 7,78 ×10−4 В/м, ϕ = −12145 В.
67
Пример 4. Определить потенциал и напряженность электрического поля, создаваемого тонким диском радиуса r , равномерно заряженного с поверхностной плотностью заряда σ , в точке C , лежащей на оси диска на расстоянии b от его плоскости.
Дано:
r , σ , b .
Найти: ϕ , E .
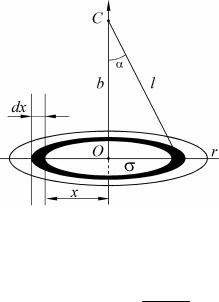
Решение. Для определения потенциала электростатического поля в точке C разобьем диск на бесконечно большое число кольцевых зон с бесконечно малой толщиной dx (рис. 1.42).
Рис. 1.42
Выделим кольцо, ограниченное радиусами x и x + dx . Разобьем выделенное кольцо на бесконечно большое число точечных элементов. Каждый точечный элемент кольца с его зарядом нахо-
дится на одинаковом расстоянии l = 
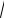 x2 + b2 от точки C , поэтому вклад каждого заряженного элемента кольца в создание потенциала в точке C одинаков. Тогда, согласно принципу суперпозиции полей, потенциал в точке C , создаваемый выделенным кольцом, будет равен [3.6]:
x2 + b2 от точки C , поэтому вклад каждого заряженного элемента кольца в создание потенциала в точке C одинаков. Тогда, согласно принципу суперпозиции полей, потенциал в точке C , создаваемый выделенным кольцом, будет равен [3.6]:
68

dj = k |
|
dq |
|
, |
|
(1) |
|
|
|
|
|
|
|||
x2 |
+ b2 |
|
|||||
|
|
|
|
|
|
||
где dq – заряд кольца, k = |
1 |
– коэффициент пропорциональ- |
|||||
|
|||||||
|
|
|
|
|
|
4pe0 |
|
ности.
Так как dq = σdS , а dS – площадь кольца, которая равна dS = 2πxdx , то заряд кольца равен dq = 2πσxdx . Выражение (1) примет вид:
dj = k 2psxdx .

 x2 + b2
x2 + b2
Интегрируя (2), определим потенциал, создаваемый диском:
|
r |
|
|
|
xdx |
|
r |
d(x2 |
+ b2 ) |
|
||||||||||||
j = 2pksò |
|
|
|
|
|
|
|
|
|
= pksò |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
x 2 + b 2 |
|
|
|
x 2 + b 2 |
|||||||||||||||
|
0 |
|
|
|
0 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
r |
æ |
|
|
|
|
|
|
|
|
|
ö |
|||
= 2pks |
x |
2 |
+ b |
2 |
|
|
|
r |
2 |
+ b |
2 |
|
|
|
||||||||
|
|
|
|
|
= 2pksç |
|
|
|
|
- b÷ . |
||||||||||||
|
|
|
|
|
|
|
|
|
0 |
è |
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(2)
(3)
Напряженность поля определяется как градиент потенциала с противоположным знаком [3.9]. Поэтому, рассматривая величину b как переменную, получим выражение:
|
dj |
æ |
|
|
|
|
|
|
b |
|
|
|
ö |
|
|
|
|
|
|
|
|
|
E = - |
= 2pksç1 |
- |
|
|
|
|
|
|
|
|
÷ . |
|
|
|
|
|
|
|
(4) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
db |
ç |
|
|
|
|
r |
2 |
+ b |
2 |
÷ |
|
|
|
|
|
|
|
|
|||
|
è |
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
||||||
|
|
æ |
|
|
|
|
|
|
|
|
|
|
ö |
æ |
|
|
|
|
b |
|
ö |
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
||||||
Ответ: j = 2pksç |
|
r |
|
+ b |
|
- b÷ |
, E = 2pksç1 |
- |
|
|
|
|
|
÷ . |
||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
è |
|
|
|
|
|
|
|
|
|
|
ø |
ç |
|
|
r |
2 |
+ b |
2 |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
ø |
||
Пример 5. Определить зависимость напряженности электростатического поля, создаваемого равномерно заряженной сферической поверхностью, несущей заряд q , радиусом R как функ-
цию расстояния от центра сферической поверхности.
Дано: q , R .
Найти: E(r).
69
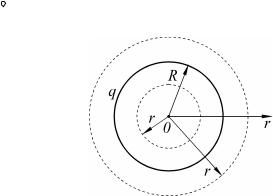
Решение. Электростатическое поле, создаваемое сферической поверхностью, центрально-симметричное: направление вектора
напряженности E в любой точке проходит через центр сферы, а модуль вектора зависит только от расстояния r до центра сферы.
Нахождение напряженности поля заряда, который нельзя считать точечным, с использованием выражения, определяющего эту физическую величину, представляет собой трудоемкий процесс. Для симметричных заряженных тел использование теоремы Гаусса [2.3] значительно упрощает задачу.
Для расчета поля заряженной сферы в качестве замкнутой поверхности удобно взять концентрическую сферу. Пусть ее радиус r > R (рис. 1.43), тогда, согласно теореме Гаусса, поток вектора напряженности электростатического поля через замкнутую поверхность равен отношению заряда, охваченного выбранной поверхностью, к электрической постоянной e0 :
r |
r |
|
q |
. |
(1) |
|
ò E × dS |
= |
|||||
|
||||||
S |
|
|
e0 |
|
||
Рис. 1.43
Так как площадь поверхности сферы радиуса r равна 4pr 2 , то теорема Гаусса для условий задачи приобретает вид:
Er × 4pr 2 = |
q |
, |
|
||
|
e0 |
|
откуда искомая напряженность как функция расстояния от центра сферы (r > R) может быть выражена в виде:
70
