
- •4. Классическое определение вероятности.
- •5. Геометрические вероятности и статистическая вероятность.
- •6. Теоремы сложения и умножения вероятностей..
- •48. Основные понятия дисперсионного анализа.
- •7. Условная вероятность.
- •8. Независимость событий.
- •9. Формулы полной вероятности и Байеса.
- •47. Критерии согласия Пирсона и Колмогорова.
- •17. Случайные величины и законы их распределения
- •21 Мода и медиана
- •22.Моменты случайных величин
- •26. Закон Пуассона.
- •27. Геометрическое и гипергеометрическое распределения.
- •28. Равномерное распределение.
- •31.Функция Лапласа.
- •38. Центральная предельная теорема.
- •Вопрос 39. Предмет математической статистики.
- •Вопрос 40. Генеральная и выборочная совокупность.
- •2. Алгебра событий.
- •11.Формула Бернулли.
- •30.Нормальный закон распределения Непрерывная случайная величина х имеет нормальный закон распределения (закон Гаусса) с параметрами а и , если ее плотность вероятности имеет вид
- •13.Теорема Пуассона.
- •15. Случайные величины их класификация
- •29.Показательное распределение.
- •16.Дискретные и Непрерывные величины.
- •37. Теорема Чебышева и Бернулли.
- •23.Асимметрия и эксцесс.
- •25.Биномиальный закон распределения.
- •26.Функции случайных величин.
- •33. Многомерные случайные величины.
- •14. Локальной и интегральной формуле Муавра – Лапласа
- •3 Частота и вероятность
- •35. Корреляционный момент и коэфф.Корреляции.
- •34 Зависимые и независимые случайные величина.
- •12.Найвераятнейшее число успехов в схеме Бернулли.
- •10. Последовательность независимых повторных испытаний.
- •32. Распределение «хи-квардат». Стьюдента и Фишера –Снедекора.
- •44. Статистические гипотизы.
- •43. Предельная ошибка и необходимость объем выборки.
- •45. Уровень значимости и мощность критерии.
- •46. Проверка статистических гипотез.
- •53. Ранговая корреляция
- •52. Проверка значимости уравнение и коэффициентов уравнения регрессии.
- •50. Модели и Основные понятия корреляционного и регрессионного анализа
- •51. Линейная корреляционная зависимость и линии регрессии.
- •49. Однофакторный дисперсионный анализ
37. Теорема Чебышева и Бернулли.
Теорема
Чебышева.
Если
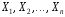 последовательность независимых случайных
величин с математическими ожиданиями
последовательность независимых случайных
величин с математическими ожиданиями
 и дисперсиями
и дисперсиями
 ,
ограниченными одной и той же постоянной
,
ограниченными одной и той же постоянной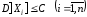 ,
то какова бы ни была постоянная
,
то какова бы ни была постоянная
 .
.
При доказательстве предельного равенства используется неравенство
 ,
,
которое вытекает из неравенства Чебышева.
Теорема
Бернулли.
При неограниченном увеличении числа
независимых опытов частость появления
 некоторого
событияА
сходится по вероятности к его вероятности
р = Р(А):
некоторого
событияА
сходится по вероятности к его вероятности
р = Р(А):
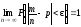 ,
где
,
где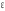 —
сколь угодно малое положительное число.
—
сколь угодно малое положительное число.
При
доказательстве теоремы Бернулли получаем
такую оценку

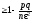 ,
которая применяется на практике.
,
которая применяется на практике.
23.Асимметрия и эксцесс.
Вычисление
асимметрии и эксцесса позволяет
установить симметричность распределения
случайной величины Х относительно
M(X)=1 Для
этого находят третий центральный момент,
характеризующий асимметрию закона
распределения случайной величины. Если
он равен нулю µ3=0 ,
то случайная величина x
симметрично распределена относительно
математического ожидания M(X) Поскольку
µ3 имеет
размерность случайной величины в кубе,
то вводят безразмерную величину
— коэффициент
асимметрии:
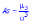
Центральный момент четвертого порядка используется для определения эксцесса, характеризует вершину плотности вероятности F(x) Эксцесс вычисляется по формуле
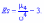
Число
3 вычитается для сравнения отклонения
от центрального закона распределения
(нормального закона), для которого
подтверждается равенство:
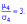
25.Биномиальный закон распределения.
Биномиальное распределение
Пусть имеется n испытаний Бернулли с вероятностью успеха p и вероятностью неуспеха q, p+q=1. Дискретная случайная величина Х – число успехов имеет распределение
Pk = P(Х = K)=Cnk pkqn-k, k=0,1……,n.
Это распределение называется биномиальным с параметрами p и q
Математическое ожидание и дисперсия случайной велчины
MX = np, DX = npq.
26.Функции случайных величин.
Случайной величиной называется функция Х на пространстве событий Ω такая, что для всякого числа х подмножество (Х< х) является событием.
Функцией распределения случайной величины Х называется функция у=F(x), значение которой определяются формулой
F(x)=P(Х< х)
Где P(Х< х) – вероятность событий (Х< х)
Для
дискретной случайной величины Х с
законом распределения P(Х<
хk)=pk
,k=1,2,…..,функция
распределения имеет вид 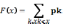

Графиком функции распределения дискретной случайной величины является график кусочно-постоянной функции. Скачки функции F(x) в точке разрыва х=хk равны PK=p(x = Xk).
Функцией распределения непрерывной случайной величины
P(a < X <b) = F (b) – F(a)
Из этого следует что вероятность каждого конкретного значения непрерывной случайной величины равна нулю.
33. Многомерные случайные величины.
Многомерной случайной величиной наз. величина, которая при проведении опыта принимает в качестве своего значения не число, а целый набор чисел, заранее не известно каких. Эти наборы, которые случайная величина может принять, образуют множество ее возможных значений. Таким образом, хотя конкретный набор не предугадаешь, он будет из множества возможных наборов (часто это множество хорошо известно).
Понятие
многомерной случайной величины аналогично
таким понятиям, как система случайных
величин или многомерный случайный
вектор. Каждое элементарное событие
может рассматриваться, как результат
сложного испытания, состоящего в
измерении всех величин  и
интерпретироваться, как точка
и
интерпретироваться, как точка  –
мерного пространства (
–
мерного пространства ( )
или, как вектор
)
или, как вектор 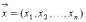 .
Каждая из величин
.
Каждая из величин  является
одномерной случайной величиной и
называется составляющей (компонентой).
Если говорят, что
является
одномерной случайной величиной и
называется составляющей (компонентой).
Если говорят, что  –
случайный вектор (или
–
случайный вектор (или  –
мерная случайная величина), то
величины
–
мерная случайная величина), то
величины  называют
его случайными координатами. Аналогично
одномерным случайным величинам различают
дискретные многомерные случайные
величины (их составляющие дискретны) и
непрерывные многомерные случайные
величины, которые устроены более сложно
(их составляющие непрерывны).
называют
его случайными координатами. Аналогично
одномерным случайным величинам различают
дискретные многомерные случайные
величины (их составляющие дискретны) и
непрерывные многомерные случайные
величины, которые устроены более сложно
(их составляющие непрерывны).
