
- •4. Классическое определение вероятности.
- •5. Геометрические вероятности и статистическая вероятность.
- •6. Теоремы сложения и умножения вероятностей..
- •48. Основные понятия дисперсионного анализа.
- •7. Условная вероятность.
- •8. Независимость событий.
- •9. Формулы полной вероятности и Байеса.
- •47. Критерии согласия Пирсона и Колмогорова.
- •17. Случайные величины и законы их распределения
- •21 Мода и медиана
- •22.Моменты случайных величин
- •26. Закон Пуассона.
- •27. Геометрическое и гипергеометрическое распределения.
- •28. Равномерное распределение.
- •31.Функция Лапласа.
- •38. Центральная предельная теорема.
- •Вопрос 39. Предмет математической статистики.
- •Вопрос 40. Генеральная и выборочная совокупность.
- •2. Алгебра событий.
- •11.Формула Бернулли.
- •30.Нормальный закон распределения Непрерывная случайная величина х имеет нормальный закон распределения (закон Гаусса) с параметрами а и , если ее плотность вероятности имеет вид
- •13.Теорема Пуассона.
- •15. Случайные величины их класификация
- •29.Показательное распределение.
- •16.Дискретные и Непрерывные величины.
- •37. Теорема Чебышева и Бернулли.
- •23.Асимметрия и эксцесс.
- •25.Биномиальный закон распределения.
- •26.Функции случайных величин.
- •33. Многомерные случайные величины.
- •14. Локальной и интегральной формуле Муавра – Лапласа
- •3 Частота и вероятность
- •35. Корреляционный момент и коэфф.Корреляции.
- •34 Зависимые и независимые случайные величина.
- •12.Найвераятнейшее число успехов в схеме Бернулли.
- •10. Последовательность независимых повторных испытаний.
- •32. Распределение «хи-квардат». Стьюдента и Фишера –Снедекора.
- •44. Статистические гипотизы.
- •43. Предельная ошибка и необходимость объем выборки.
- •45. Уровень значимости и мощность критерии.
- •46. Проверка статистических гипотез.
- •53. Ранговая корреляция
- •52. Проверка значимости уравнение и коэффициентов уравнения регрессии.
- •50. Модели и Основные понятия корреляционного и регрессионного анализа
- •51. Линейная корреляционная зависимость и линии регрессии.
- •49. Однофакторный дисперсионный анализ
14. Локальной и интегральной формуле Муавра – Лапласа
Локальная теорема Муавра-Лапласа.
Вычисление
вероятности
 по формуле Бернулли становится
затруднительным при больших
по формуле Бернулли становится
затруднительным при больших ,
поскольку
,
поскольку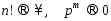 .
Поэтому на практике применяют приближенные
формулы. Одна из них формула Муавра-Лапласа.
.
Поэтому на практике применяют приближенные
формулы. Одна из них формула Муавра-Лапласа.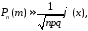
где

Функция
 - четная:
- четная: ;
достигает максимума
;
достигает максимума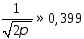 в точке
в точке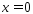 .
При этом
.
При этом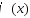 быстро стремится к нулю с увеличением
абсолютной величины
быстро стремится к нулю с увеличением
абсолютной величины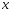 :
:
Интегральная формула Муавра-Лапласа.
Если
нас интересует вероятность того, что в
серии из
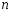 испытаний событие
испытаний событие появится не менее
появится не менее и не более
и не более раз, то
раз, то
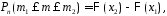
где

Здесь
 - функция Лапласа. Функция
- функция Лапласа. Функция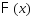 нечетная
нечетная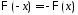 .
При возрастании
.
При возрастании от 0 до
от 0 до функция
функция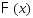 быстро возрастает почти до 0,5.
быстро возрастает почти до 0,5. ,
,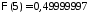 .
Можно считать
.
Можно считать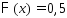 при всех
при всех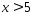 .
.
3 Частота и вероятность
Вероятностью
события A
называют отношение числа благоприятствующих
этому событию исходов к общему числу
всех единственно возможных и равновозможных
исходов испытания.
Относительной
частотой
события называют отношение числа
испытаний, в которых событие появилось
к общему числу фактически произведенных
испытаний.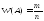
Вероятность вычисляют до опыта, а относительную частоту — после.
В различных опытах относительная частота изменяется мало (тем меньше, чем больше произвели испытаний) и колеблется возле некоторого постоянного числа — вероятности.
35. Корреляционный момент и коэфф.Корреляции.
Корреляционным
моментом
 случайных величин X
и Y
называют математическое ожидание
произведения их отклонений.
случайных величин X
и Y
называют математическое ожидание
произведения их отклонений.
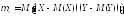
Для дискретных величин
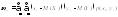
Для непрерывных величин

Теорема. Корреляционный момент двух независимых случайных величин равен 0
Коэффициентом корреляции независимых случайных величин X и Y называют отношение корреляционного момента к произведению средних квадратических отклонений этих величин.

34 Зависимые и независимые случайные величина.
Случайные события называются независимыми, если появление одного из них никак не влияет на вероятность появления других событий.
Для независимых событий справедлива теорема умножения вероятностей: вероятность совместного (одновременного) появления нескольких независимых случайных событий равна произведению их вероятностей:
Р(А1и А2 и А3 … и Аk) = Р(А1) ∙Р(А2) ∙…∙Р(Аk). (7)
Совместное (одновременное) появление событий означает, что происходят события и А1, и А2 ,и А3 … и Аk .
Случайные события А и В называются зависимыми, если появление одного из них, например, А изменяет вероятность появления другого события – В. Поэтому для зависимых событий используются два значения вероятности: безусловная и условная вероятности.
Если А и В зависимые события, то вероятность наступления события В первым (т.е. до события А) называется безусловной вероятностью этого события и обозначается Р(В). Вероятность наступления события В при условии, что событие А уже произошло, называется условной вероятностью события В и обозначается Р(В/А) или РА (В).
Аналогичный смысл имеют безусловная – Р(А) и условная – Р(А/В) вероятности для события А.
Теорема умножения вероятностей для двух зависимых событий: вероятность одновременного наступления двух зависимых событий А и В равна произведению безусловной вероятности первого события на условную вероятность второго:
Р(А и В) = Р(А) ∙Р(В/А) , если первым наступает событие А, или
Р(А и В) = Р(В) ∙Р(А/В), если первым наступает событие В.
