47. Критерии согласия Пирсона и Колмогорова.

Пусть { x₁,x₂,….,x_n} – выборка из некоторой генеральной совокупности Х ,F (x) –предполагаемая функция теоретического распределения. На основании выборки построим интервальный ряд {Δ_i,n_i}, i=1,m, где n_i–число элементов выборки, попавших в в интервал Δ_i = [а_і, а_і+1). Для каждого интервала Δ_і вычислим теоретические вероятности Р_іпопадания случайной величины Х в интервал Δ_і:

P_i = P{xϵΔ_i} = F(a_i+ 1) – F(a_i).

Число n_iиnP_iназываются эмпирическими и теоретическими частотами. Доказано, что при n →∞ статистика t = ∑(n_i – nP_i)²/nP_i

имеет χ² – распределение с k = m-r-1 степенями свободы, где m–число интервалов вариационного ряда, r–число параметров теоретического распределения, вычисленных по экспериментальным данным.

Основная гипотеза Н₀ состоит в том, что функцией распределения случайной величины Х является выбранная нами теоретическая функция F(x).

Для заданного уровня доверия ϒ по таблицам распределенияχ²_к находим критическое значение Χ²_к,кр: Р{χ²_к<χ²_к,кр } = ϒ.

Гипотеза Н₀ о согласии экспериментальных данных с распределением F(x) принимается, если t<χ²_к,кр.

Заметим, что статистика tимеет распределение χ² при n→∞, поэтому критерий Пирсона следует применять только при большихn (n> 30).

Критерий Колмогорова заключается в сопоставлении эмпирических F_n(x) и теоретическихF(x) функций распределения. Колмогоров доказал, что какова бы ни была функция распределения F(x) непрерывной случайной величины Х, функция распределения статистики t = √nmax|F_n(x) – F(x)| при n→∞ стремится к функции К(х) = 1 - ∑ (-1)^ke^-2k2x2.

Задавая доверительную вероятность ϒ, из соотношения К(х) = ϒ можно найти критическое значение х_кр.

Гипотеза Н₀о согласии экспериментальных данных с функцией распределения F(х)принимается на уровне ϒ, если t<t_кр.

В критерии Колмогорова параметры закона распределения F(x) считаются известными заранее, так что заменяя их на выборочные значения, мы всегда привносим некоторую ошибку.

17. Случайные величины и законы их распределения

Опытом называется всякое осуществление определенных условий и действий при

которых наблюдается изучаемое случайное явление. Опыты можно характеризовать

качественно и количественно.

Случайной называется величина, которая в результате опыта может принимать то

или иное значение., причем заранее не известно какое именно. Случайные

величины принято обозначать (X,Y,Z), а соответствующие им значения (x,y,z)

Дискретными называются случайные величины принимающие отдельные

изолированные друг от друга значения, которые можно переоценить.

Непрерывными величины возможные значение которых непрерывно заполняют

некоторый диапазон.

Законом распределения случайной величины называется всякое соотношение

устанавливающее связь между возможными значениями случайных величин и

соответствующими им вероятности.

Ряд и многоугольник распределения.

Простейшей формой закона распределения дискретной величины является ряд

распределения.

x	x1	x2	x3
P	P1	P2	P3

Графической интерпретацией ряда распределения является многоугольник

распределения.

18.Функция распределения случайной величины.

Для непрерывных случайных величин применяют такую форму закона распределения,

как функция распределения.

Функция распределения случайной величины Х, называется функцией аргумента х,

что случайная величина Х принимает любое значение меньшее х (Х<х)

F(х)=Р(Х<х)

F(х) - иногда называют интегральной функцией распределения или интегральным

законом распределения.

Функция распределения обладает следующими свойствами:

1. 0<F(х)<1

2. если х₁>х₂,то F(х₁)>F(х₂)

3.

функция может быть изображена в виде графика. Для непрерывной величины это

будет кривая изменяющееся в пределах от 0 до 1, а для дискретной величины -

ступенчатая фигура со скачками.

С помощью функции распределения легко находится вероятность попадания

величины на участок от α до β

Р(α<х<β) рассмотрим 3 события

А - α<Х

В - α<Х<β

С - Х<β

С=А+В

Р(С)=Р(А)+Р(В)

Р(α<х<β)=Р(α)-Р(β)

19. Плотность распределения вероятности непрерывной случайной величины.

Плотность распределения вероятности непрерывной случайной величины Х

называется функция f(х) равная первой производной от функции распределения

F(х)

График плотности распределения называется кривой распределения.

Основные свойства плотности функции распределения:

1. f(х)>0

2.

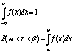
111Equation Chapter 1 Section 1 20 Математическое ожидание и дисперсия случайной величины

Математическим ожиданием дискретной случайной величины называется сумма произведений всех ее возможных значений на соответствующие вероятности. Математическое ожидание случайной величины обозначается через М(Х), или или а. Если дискретная случайная величина принимает конечное число значений х1, х2,…хn соответственно с вероятностями р1, р2,…рn, то по определению М(Х) = х1р1+х2р2+... + хnpn,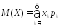

Выясним вероятностный смысл математического ожидания дискретной случайной величины. Пусть в результате n испытаний случайная величина X значение Х1 приняла m1раз, значение х2 – m2 раз, значение хк - mк раз, причем m1 + m2 +... + mk =n. Так как сумма принятых значений равна x1m1 + х2m2 +... + хкmк то среднее арифметическое х всех ее значений определяется формулой

X=х1m1+ х2m2 +... + хкmк /n или x=x1*m1/n+x2*m2/n+….+xkmk/n, x=x1W1+x2W2+….+xkWk, где Wj =mi/n относительная частота значений xi (i = 1, 2, ..,, к). Если n достаточно велико, то относительная частота события приближенно равна его вероятности, т.е. Wk = рк, поэтому получаем приближенную формулу x=x1p1+x2p2+…+xkpk,

Итак, математическое ожидание дискретной случайной величины приближенно равно среднему арифметическому ее возможных значений. Вследствие этого математическое ожидание случайной величины называется ее средним значением.

Замечание.

Математическое ожидание называют также центром распределения. Это название заимствовано из механики и объясняется следующим: если в точках х1,х2,...,хп оси Ох находятся соответственно массы P1Р2,…Рn то координата х центра тяжести системы материальных точек вычисляется по формуле : () . Так как=1, то

Дисперсией, или рассеянием, случайной величины X называется математическое ожидание квадрата ее отклонения. Дисперсия обозначается через D(X), т.е.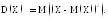Из определения и свойств математического ожидания следует, что дисперсия любой случайной величины X неотрицательна, т.е.Для вычисления дисперсии применяется формула