32. Распределение «хи-квардат». Стьюдента и Фишера –Снедекора.

Распределении.

Пусть Х₁, Х₂, …, Х_n- независимые нормально распределенные случайные величины с нулевыми математическими ожиданиями и средними квадратичными отклонениями, = 1. Тогда закон распределения суммы квадратов случайных величин. Χ²=Х²₁+Х²₂+…+Х²_n наз.законом хи-квадрат с n степенями свободы.

Плотность вероятности такой случайный величины имеет вид.

Где Г (n/2)- гамма-функция, для которой выполняется равенство Г(n+2)= n!

Распределение стьюдера

Пусть Х0,Х₁, Х₂, …, Х_n- независимые нормально распределенные случайные величины с нулевыми математическими ожиданиями и средними квадратичными отклонениями, = 1.

Тогда случайная величинаИмеет распределение Стьюдента (t-распределение) с n степенями свободы.

Плотность вероятности случайной величины Т имеет вид f(x)= b_n(1+x²/n)- ^(n+1)/2

Где b_n= Г [(n+1)/2]/ Г(n/2)√πn

Распределение Фишера-Снекорда.

Пусть Х₁, Х₂, …, Х_n и Y1,Y2,…, Ym- независимые нормально распределенные случайные величины с нулевыми математическими ожиданиями и средними квадратичными отклонениями, = 1.Тогда случайная величина

Имеет распределение Фишера-Снедекора с n и m степенями свободы.

44. Статистические гипотизы.

Пусть Х  наблюдаемая дискретная или непрерывная случайная величина.

Статистической гипотезой Н наз. некоторое предположение относительно параметров или вида распределения случайной величины Х, проверяемое по выборочным данным.

Примеры гипотез:

1) генеральная случайная величина Х имеет математическое ожидание M (X)=m0 и дисперсию D(X)=σ ₀² ;

2)случайная величина Х, распределённая по показательному закону, имеет параметр λ = 1;

3) случайная величина Х распределена по нормальному закону N (0, 1) ;

4) случайная величина Х распределена по закону Пуассона.

43. Предельная ошибка и необходимость объем выборки.

Предельная ошибка выборкиравна t-кратному числу средних ошибок выборки:

  

μ– средняя ошибка выборки, рассчитанная с учетом поправки, на которую производится корректировка в случаебесповторного отбора;

t – коэффициент доверия, который находят при заданном уровне вероятности. Так для Р=0,997 по таблице значений интегральной функции Лапласа t=3

Величина предельной ошибки выборкиможет быть установлена с определеннойвероятностью. Вероятность появления такой ошибки, равной или больше утроенной средней ошибки выборки, крайне мала и равна 0,003 (1–0,997). Такие маловероятные события считаются практически невозможными, а потому вероятность того, что эта разность превысит трехкратную величину средней ошибки, определяетуровень ошибкии составляет не более0,3%.

В практике организации выборочного наблюдения возникает потребность определения необходимой численности (объема) выборкидля обеспечения заданной точности предельной ошибки выборки и ее вероятности. Определение необходимой численности (объема) выборки основывается на формуле предельной ошибки выборки.

Из формулы предельной ошибки выборки среднего значения признака при повторном отборе:

 находим    

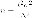
При бесповторномслучайном отборе необходимая численность выборки вычисляется по формуле:

  

При типическойвыборке:

  

При серийнойвыборке:

  

Необходимый объем (численность) выборки при определении долиисчисляется по аналогичным формулам с той разницей, что вместо дисперсииколичественного признака, используется дисперсияальтернативного признака. Так, для случайной бесповторной выборки формула необходимой численности выборки будет иметь следующий вид: