27. Геометрическое и гипергеометрическое распределения.

Дискретная случайная величина Х имеет геометрическое распределение, если она принимает значения k=1, 2, 3, … с вероятностями

Определение является корректным, т.к. сумма вероятностей

Случайная величина Х, имеющая геометрическое распределение, представляет собой число испытаний Бернулли до первого успеха.

Математическое ожидание и дисперсия Х:

Дискретная случайная величина Х имеет гипергеометрическое распределение, если она принимает значения m с вероятностями гдеm=0,1,…,k; k = min(n, M); MN; nN.

Вероятность является вероятностью выбораm объектов обладающих заданным свойством, из множества n объектов, случайно извлечённых (без возврата) из совокупности N объектов, среди кот. Mобъектов обладают заданным свойством.

Математическое ожидание и дисперсия случайной величины, имеющей гипергеометрическое распределение с параметрамиn, M, N:

28. Равномерное распределение.

Непрерывная случайная величина Х распределена равномерно на отрезке [a;b], если её плотность вероятности p(x) постоянна на этом отрезке и равна нулю вне его, т.е.

Функция распределения случайной величины, распределённой по равномерному закону, имеет вид

Математическое ожидание и дисперсия равномерной случайной величины: .

31.Функция Лапласа.

Определение. Нормальное распределение с параметрами а = 0, σ = 1 называется нормированным, а его функция распределения

- функцией Лапласа.

Замечание. Функцию распределения для произвольных параметров можно выразить через функцию Лапласа, если сделать замену:

, тогда

Вероятность попадания нормально распределенной случайной величины на

заданный интервал равна:

38. Центральная предельная теорема.

Центральная предельная теорема

Пусть последовательность одинаково распре­делённых случайных величин с математическими ожиданиями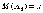и дисперсиями.

ТЕОРЕМА. Если случайные величины независимы и, то при достаточно большомn закон распределения суммы будет сколь угодно близок к нормальному закону распределения.

Так как в условиях теоремы случайные величины независимы, то

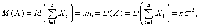
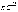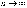т.е. в условиях теоремы сумма имеет закон распределения близкий к.Так' какna и  с ростом п, возрастают, то удобнее рассматривать не просто суммы , а нормированные суммы. Такие суммы приимеют закон распределения.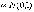

Если случайная величина может быть представлена в виде суммы большого числа независимых (или слабо зави­симых) случайных величин, каждая из которых мала по сравнению с суммой, то эта сумма имеет закон распределения близкий к нормальному.

Вопрос 39. Предмет математической статистики.

Предметомматем. статистики явл. изучение случайных событий и случайных величин по результатам наблюдений. Статистической совокупностьюназывается совокуп. предметов или явлений, объединенных каким-либо общим признаком. Результатом наблюдений над статист.совокуп. явл. статистические данные – сведения о том, какие значения принял в итоге наблюдений интересующий нас признак (случ. величина Х).

Обработка статист.данных методами матем. статистики приводит к установлению определенных закономерностей, присущих массовым явлениям. При этом точность статистис. выводов повышается с ростом числа наблюдений.

Статис. данные, как правило, представляют собой ряд значений {х1, х2,…..,хn}некоторый случайной величины Х. Исследование случайной величины начинается с обработки этого ряда значений. Затем строятся функции, характер.случайную величину. Эти функции назыв. статистиками.

Т.о., статистика – это функция

Т : (х1, х2,…..хn)→ Т (х1, х2,…..хn),

которая набору значений {х1, х2,…..,хn} случайной величины сопоставляет по некоторому правилу действительное число. Статистика явл. функцией от реализаций случайной величины.

В теорет. исследованиях удобно рассматривать статистикуТкак функцию от случайных величин Х1, Х2, ….., Хn, имеющих такое же распределение, как и случайная величина Х:

Т =Т(Х1, Х2,…..Хn).

Т.о., мы рассматриваем случайную величину Х как набор одинаковых случайных величин {Х1, Х2,…..Хn}. В такой трактовке статистика становится случайной величиной и изучение ее распределения приводит к выводам о распределении самой случайной величины Х.