Статистическое оценивание параметров распределения

Естественно возникает задача: как оценить (найти приближенное значение) параметра (параметров), которым определяется распределение?

Если генеральную совокупность описывает параметр , то выборку – егостатистическая оценка , которая вычислена по выборке. Например, выборочное среднееоценивает генеральную среднюю; выборочная дисперсияоценивает генеральную дисперсию. Статистики принято обозначать латинскими буквами,, а параметры – греческими,.

Если статистическая оценка параметра характеризуется одним числом, она называется точечной.

Для каждой конкретной выборки точечная статистическая оценка – это число, т.е. точка на числовой оси.

Статистическая оценка являетсяслучайной величиной и меняется в зависимости от выборки.

Для одной и той же неизвестной величины можно составить бесконечно много различных оценок. Например, в качестве оценки математического ожидания нормального распределения могут служить выборочное среднее, выборочная медиана, полусумма крайних элементов.

В силу многообразия оценок, применяемых для оценивания одной и той же неизвестной величины, возникает задача выбора лучшей оценки параметра в определенном смысле. Выбор оценки из множества возможных оценок должен определятьсяследующими критериями (их предложил Р.А. Фишер).

1. Оценка должна бытьнесмещенной, т.е. ее математическое ожидание должно быть равно оцениваемому параметру.

2. Если имеются несколько несмещенных оценок для , тогда выбирают ту из них, которая обладает наименьшей дисперсией (при заданном объеме выборки). Такая оценка называетсяэффективной.

2. Точечные оценки параметров генеральной совокупности

Среднее арифметическое представляет собой несмещенную оценку математического ожидания генеральной совокупности.

Выборочная дисперсия является смещенной оценкой генеральной дисперсии .

Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия , где- поправочный коэффициент.

При больших значенияибудут мало отличаться, поэтому «исправление» выборочной дисперсии производят при малых (). В целях повышения надежности полученной оценки следует увеличивать объем выборки.

Пример 1. При обследовании 50 членов семей получен дискретный вариационный ряд.

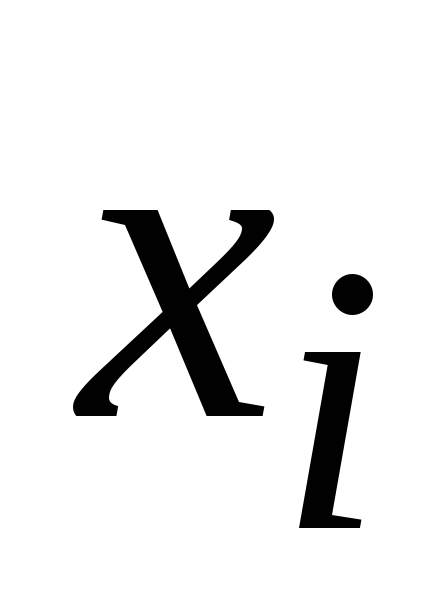
	1	2	3	4	5	6	7	8	9
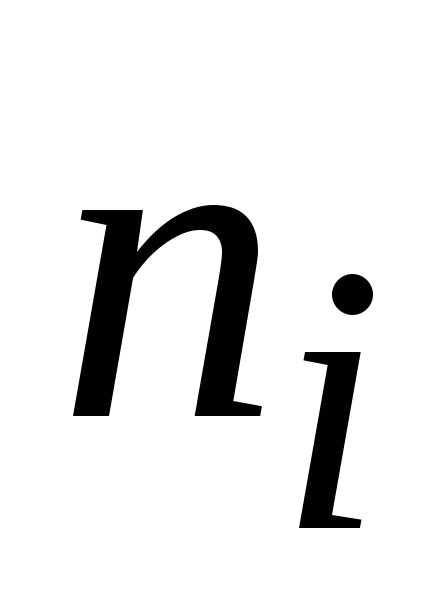
	2	4	6	8	10	9	6	4	1

Определите средний размер (среднее число членов) семьи.

Охарактеризуйте изменчивость размера семьи.

Объясните полученные результаты, сделайте выводы.

Решение

1. В данной задаче изучаемый признак является дискретным, так как размер семей не может отличаться друг от друга менее чем на одного человека. Рассчитаем среднее число членов семьи:

.

Средний размер семьи около 5 человек.

2. Для расчета дисперсии используем формулу :

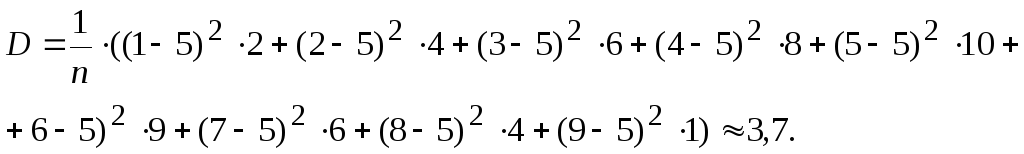
Дисперсия размера семьи – 3,7 ().

Найдем среднее квадратическое отклонение размера семьи: . Среднее квадратическое отклонение размера семьи - 2 человека.

Найдем коэффициент вариации размера семьи по формуле . Коэффициент вариации составляет 38%. Так как коэффициент вариации больше 35%, можно сделать вывод о том, что изучаемая совокупность семей являетсянеоднородной, чем объясняется высокая изменчивость размера семьи в данной совокупности.