Тестовые задания

1. Дополните. Число, показывающее, сколько раз значение признака встречается в выборке - ….

2. Ломаная, отрезки которой соединяют точки с координатами , где- значение признака,- частота:

1) многоугольник распределения, 2) гистограмма, 3) полигон.

3. Из генеральной совокупности извлечена выборка объема :

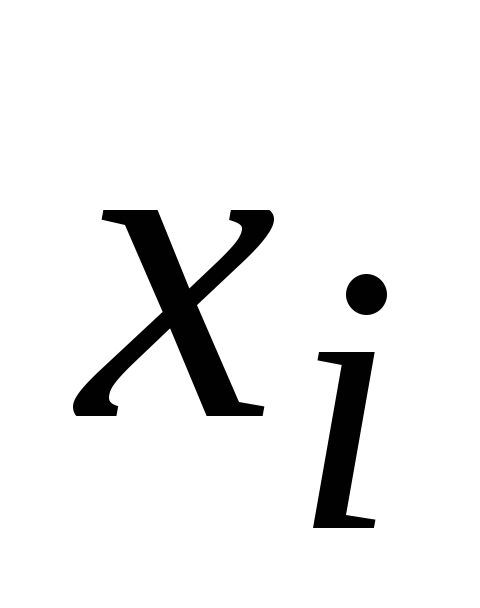
	1	2	3	4
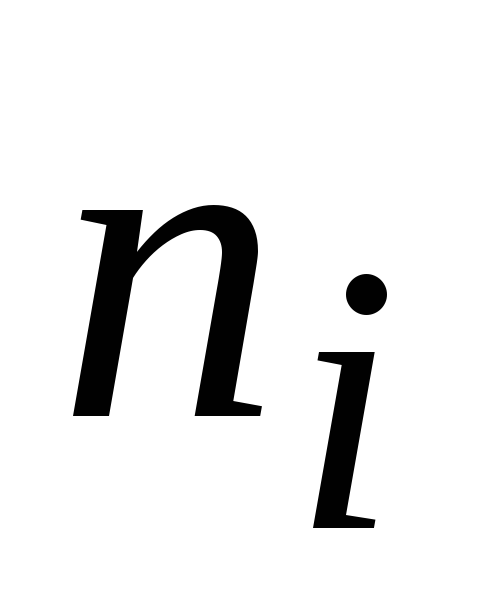
	10	9	8

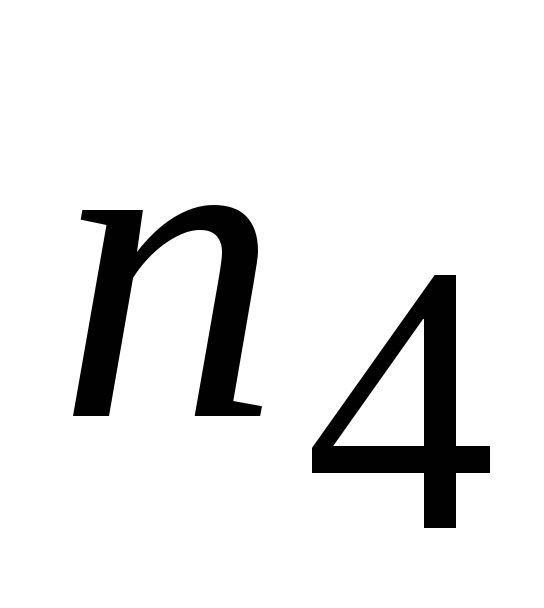
Значение равно:

1) 7; 2) 24; 3) 23; 4) 50.

4. Отношение частоты значения признака к объему выборки - это …

5. Фигура, составленная из прямоугольников с основаниями, равными интервалам значений признака, и высотами, равными соответствующим частотам:

1) многоугольник распределения, 2) гистограмма, 3) полигон.

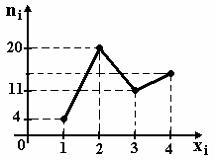
6. Из генеральной совокупности извлечена выборка объема n=50, полигон частот которой имеет вид. Тогда число вариант в выборке равно:

1) 50; 2) 15; 3) 16; 4) 14.

7. Сумма частот выборочных значений признака равна:

1) единице;

2) объему выборки;

3) ;

4) .

Ответы. 1. частота. 2. полигон. 3. 23. 4. 15.

5. относительная частота. 6. гистограмма. 7. объему выборки.

Контрольные вопросы

1. В чем заключается первичная обработка статистического материала?

2. Что такое вариационный ряд, статистический ряд?

3. Что такое группированный статистический ряд?

4. Как построить по данной выборке дискретный и интервальный сгруппированные статистические ряды?

5. Что такое полигон частот?

6. Что такое гистограмма выборки?

Тема 3. Числовые характеристики выборки

Группировка и построение частотного распределения – первый шаг статистического анализа полученных данных. Следующий шаг – получение числовых характеристик выборки.

Числовые характеристики

выборки

Средние значения Характеристика изменчивости

* среднее арифметическое * размах выборки

* медиана * выборочная дисперсия

* мода * среднее квадратическое отклонение

Важнейшими первичными статистиками, характеризующими распределение исследуемого признака, являются средняя арифметическая и среднее квадратичное отклонение.

1. Меры центральной тенденции

Основной характеристикой вариационного ряда является его среднее арифметическое. Это типическая характеристика всей совокупности. Она уничтожает, погашает, сглаживает влияние индивидуальных особенностей и позволяет представить в одной величине некоторую общую характеристику реальной совокупности.

Для дискретного выборочного ряда среднее арифметическое значений (иливыборочное среднее значение) равно

.

Чтобы подсчитать среднее арифметическое, надо суммировать все значения ряда и разделить сумму на количество суммированных значений

Если числа в выборке повторяются, например, -раз,-раз, …,-раз, причем, тодля сгруппированных выборочных данных выборочное среднее равно

и называется взвешенным средним (здесь - середина-го интервала). Для интервального вариационного ряда запринимают середину-го интервала.

Среднее арифметическое имеет двойной смысл:

1) оно может быть средним значением признака в данной совокупности (средняя зарплата отдела);

2) это приближенное значение постоянной величины, подвергающейся изменениям (рост человека).

Модой называется числовое значение признака, которое встречается в выборке с наибольшей частотой (обозначается ).

Медианой называется значение признака, которое делит упорядоченное множество данных пополам по объему (обозначается ).

Если число членов ряда нечетное (), то серединой ряда будет значение. Если число членов рядачетное (), то за медиану обычно принимают.