3. Задача оценки различия средних значений признака в независимых выборках

Задача. Преподаватель сопоставил изложение одной и той же темы в двух различных учебниках. Работая в двух параллельных студенческих группах, он отобрал из них случайным образом две группы по 15 студентов в каждой и поручил им самостоятельно проработать эту тему: одной группе по первому учебнику, другой группе – по второму.

В конце эксперимента студентам был предложен тест на усвоение изученного материала. Результаты оценивались количеством правильных ответов. Были получены следующие данные:

в первой группе ,,;

во второй группе ,,.

Значимы ли различия между средним количеством правильных ответов студентов в группах?

Решение

Нулевую гипотезу (о равенстве генеральных средних) проверим на уровне значимости. Альтернативная гипотеза(о различии) задаетдвустороннюю критическую область.

Обе выборки независимы, выборочные дисперсии равны между собой , объемы выборок совпадают (). Тогда значение

.

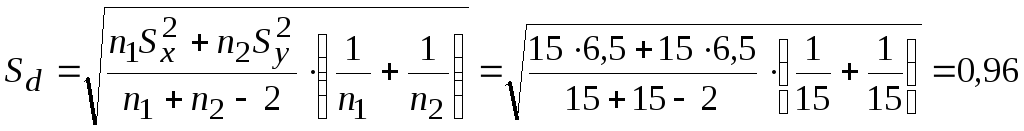Вычислим эмпирическое значение критерия:

.

Найдем по таблице критические точки -распределения Стьюдента длядвусторонней критической области при уровне значимости и числе степеней свободы. Получим. Значит, правая критическая точка, левая критическая точка, а область допустимых значений двустороннего-критерия есть симметричный интервал отдо.

Значение находится внутри области допустимых значений, то есть, поэтомунет оснований для отклонения гипотезы о равенстве генеральных средних значений числа правильных ответов в группах. Расхождение между инезначимо. Оба учебника дают примерно одинаковые результаты по усвоению учебного материалы по критерию числа правильных ответов на тестовые задания.

Тестовые задания

1. Критерий Стьюдента применяется для статистической оценки различия:

1) генеральных средних значений признака;

2) выборочных средних значений признака;

3) генеральных дисперсий признака;

4) выборочных дисперсий признака.

2. Отметьте не менее двух правильных ответов. Пусть для гипотезы о среднихальтернативная гипотезаимеет вид. По критерию Стьюдента значение, а для уровня значимости 0,05 значение. Принимается следующее статистическое решение:

1. с ошибкой 0,05 нет оснований для отклонения гипотезы о незначимости различий между генеральными средними

2. с ошибкой 0,05 можно считать различие между генеральными средними статистически незначимым (недостоверным), что объясняется случайными причинами

3. с достоверностью 0,95 принимается гипотеза о том, что «генеральное среднее выборки Х больше генеральной средней выборки У»

4. средние двух совокупностей значимо различаются с достоверностью 0,95. Различие средних значений не может быть объяснено случайными причинами

3.Отметьте не менее двух правильных ответов. Для гипотезы «о средних»альтернативная гипотезаимеет вид. По критерию Стьюдента, а для уровня значимости 0,05 значение. Статистическое решение ….

1. с достоверностью 0,95 принимается гипотеза о том, что «генеральное среднее выборки Х больше генеральной средней выборки У»

2. с достоверностью 0,95 генеральные средние совокупностей значимо различаются; имеющееся различие средних значений не может быть объяснено случайными причинами

3. с ошибкой 0,05 нет оснований для отклонения гипотезы 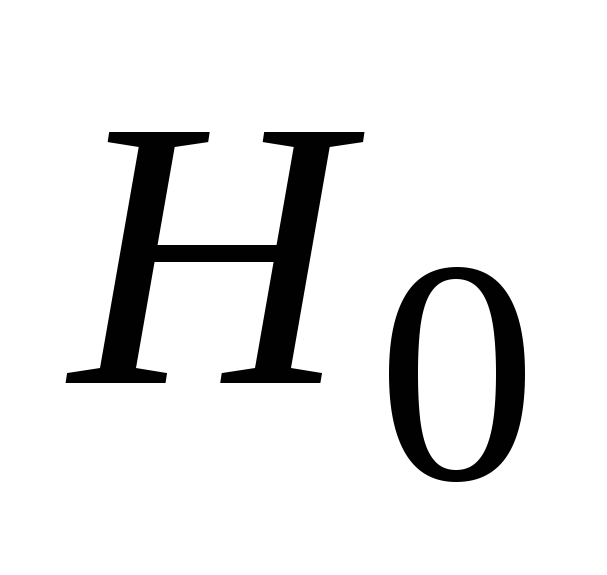о незначимости различий между генеральными средними

4. с ошибкой 0,05 можно говорить о незначимом различии между генеральными средними, что объясняется случайностью выборок

Ответы. 1.1. 2.1 и 2. 3.1 и 2.