§27. Елементи релятивістської динаміки. Взаємозв’язок маси і енергії

Другий закон Ньютона для матері­альної точки

або ,

в якому маса mточки вважається сталою і однаковою у всіх інерціальних системах відліку, виявляється не інваріантним по відношенню до перетворення Лоренца. Отже, цей закон не може служити основою релятивістської динаміки.

У релятивістській механіці, як і в ньютонівській, імпульс матеріальної точки пропорційний до її масиmі збігається за напрямком з швидкістюцієї точки. Проте, на відміну від ньютонівської механіки, імпульс матеріальної точки є не­лінійною функцією її швидкості:

,

де 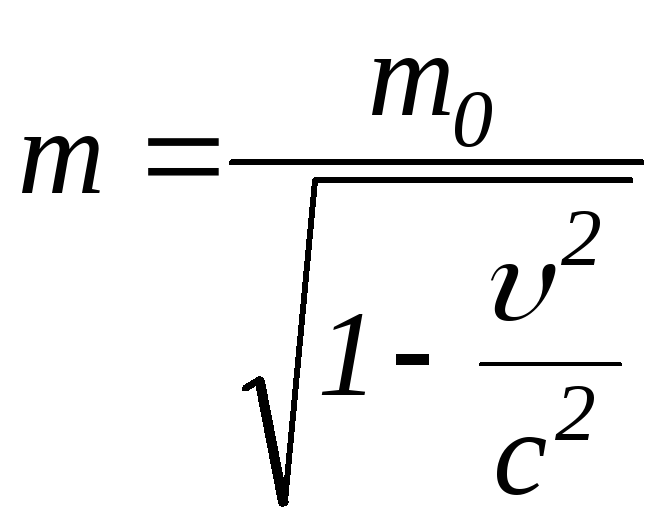– релятивістська маса, а– маса спокою матеріальної точки, тобто маса, яка виміряна в тій інерціальній системі відліку, відносно якої матеріальна точка знаходиться в стані спокою.

Основний закон релятивістської динаміки: швидкість зміни імпульсу матеріальної точки дорівнює силі , що діє на цю точку,тобто

,

.

Елементарна робота сили на малому переміщенніточки її прикладення дорівнює:

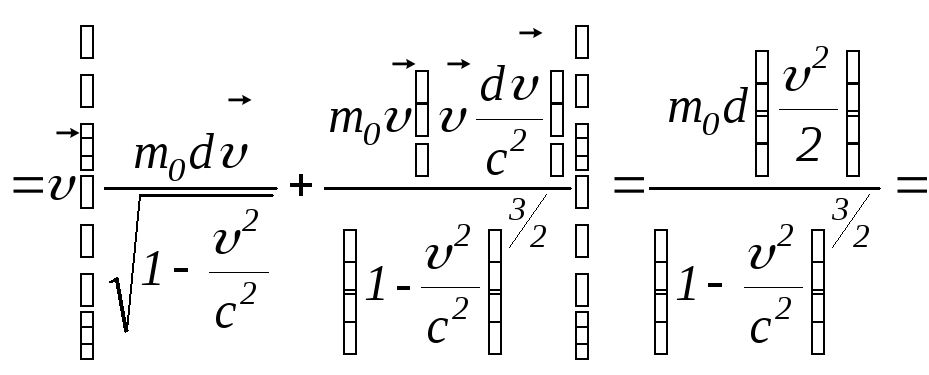
(тут враховано, що )

.

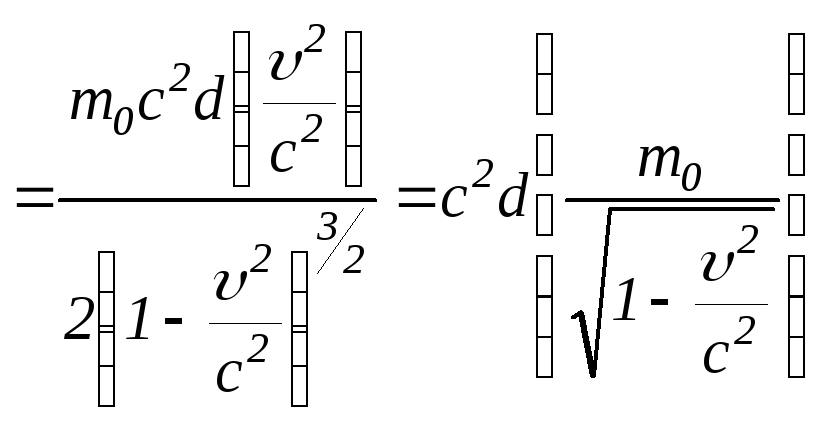Приріст кінетичної енергії матеріальної точки дорівнює роботі:

.

Інтегруючи отримане співвідношення, маємо:

.

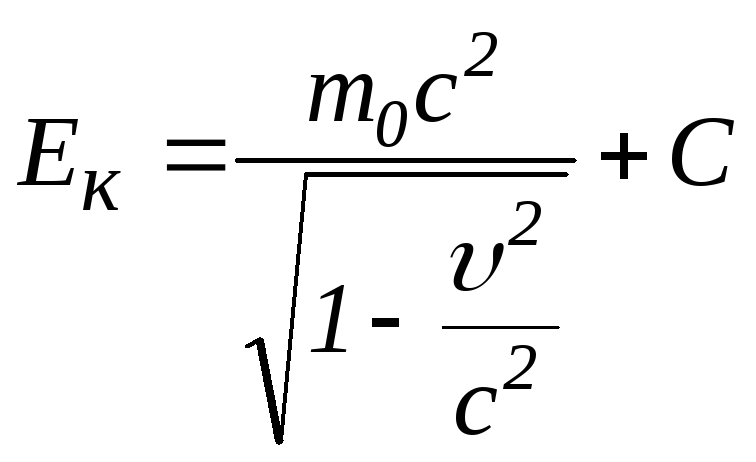При ,і.

Отже, релятивістський вираз для кінетичної енергії частинки має вигляд:

.

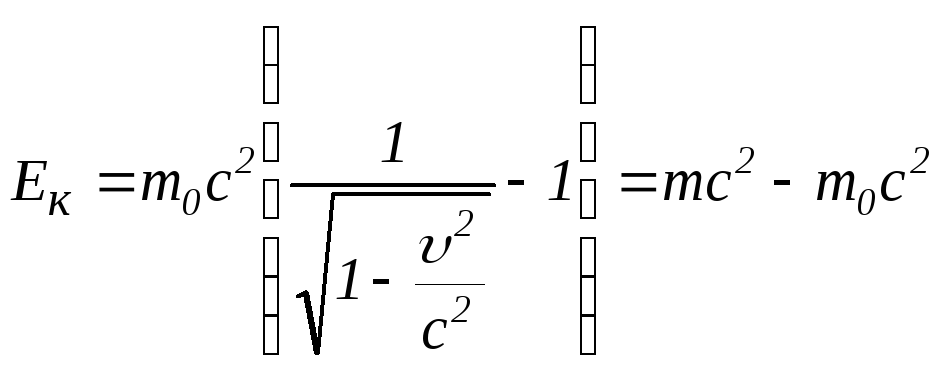При ,розкладемо в ряд, обмежившись членами другого порядку малості:

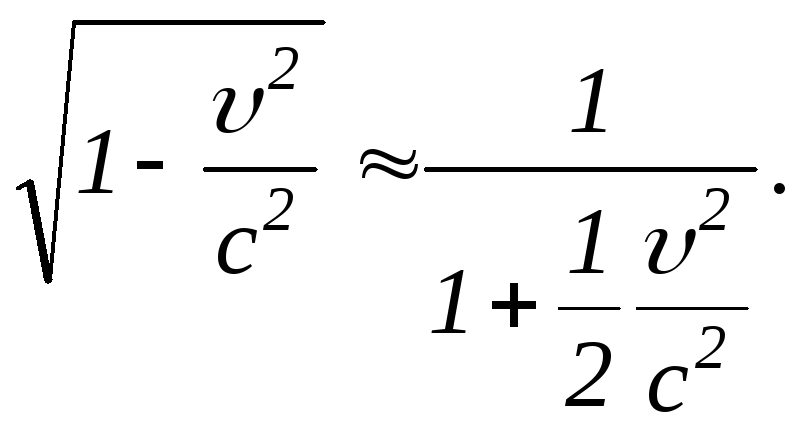
Тоді

.

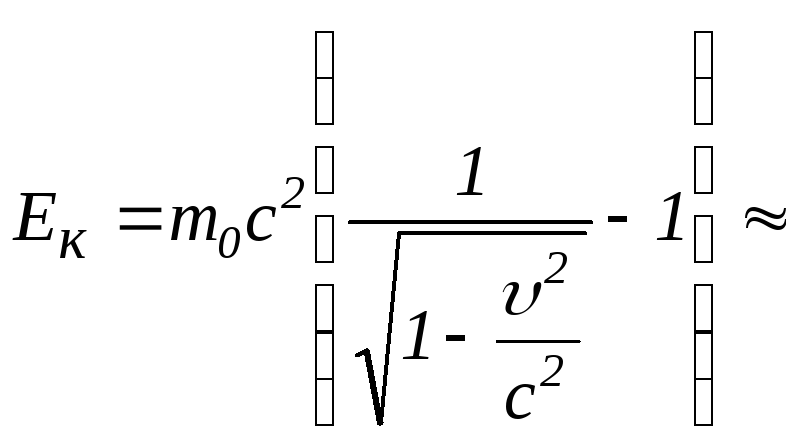
Ейнштейн узагальнив положення , передбачивши, що воно справедливе не лише для кінетичної енергії матеріальної точки, але і для повної енергії, а саме: довільна зміна маси Δ mсупроводжується зміною повної енергії матеріальної точки:

.

Звідси Ейнштейн отримав універсальну залежність між повною енергією тіла Eі його масоюm:

.

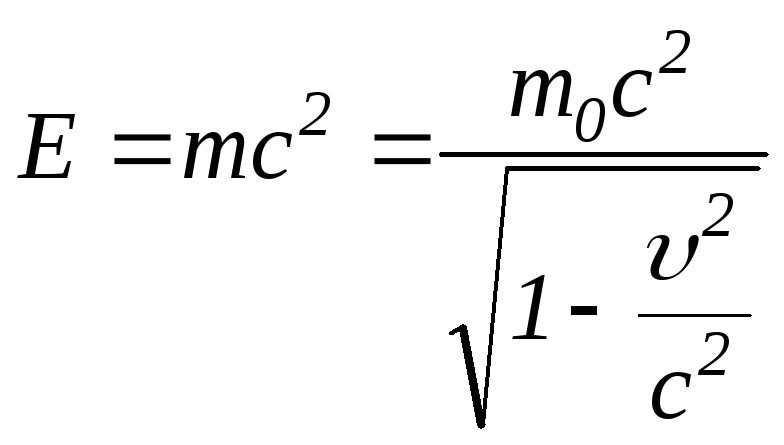Це рівняння виражає закон взаємозв’язку маси і енергії.

Знайдемо релятивістську залежність між повною енергією й імпульсом частинки:

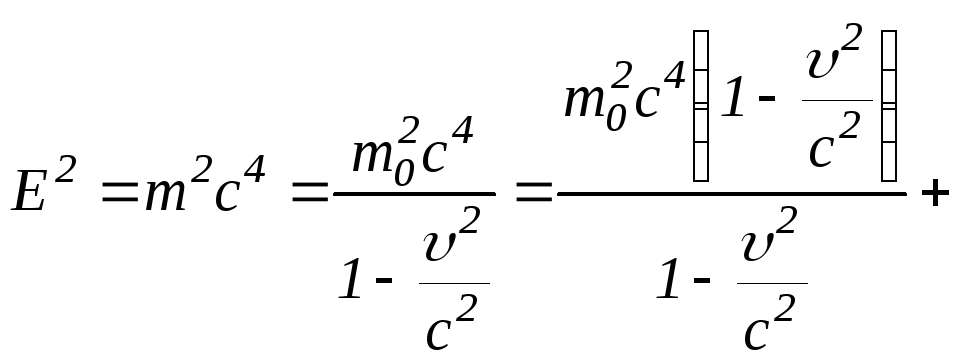
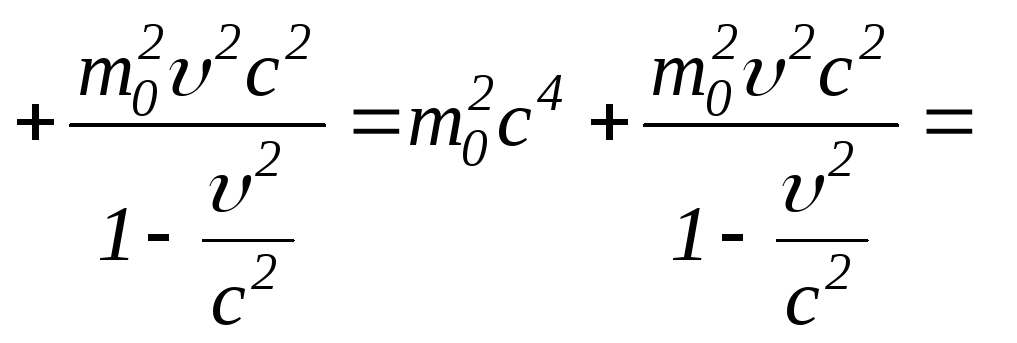
і

.

Якщо тіло нерухоме, то

,

де – енергія спокою тіла.

79