§16. Додавання взаємно перпендикулярних коливань

Нехай матеріальна точка Cодночас­но бере участь у двох гармонічних коливаннях з однаковою частотою у двох вза­ємно перпендикулярних напрямках як вздовж осіХ, так і вздовж осіY(рис. 31). Якщо збудити обидва коливання, матеріальна точка буде рухатись вздовж деякої криволінійної траєкторії, форма якої залежить від різниці фаз обох коливань.

Виберемо початок відліку часу так, щоб початкова фаза першого коливання дорівнювала нулю. Тоді рівняння коливань матимуть такий вигляд:

, .

де - різниця фаз обох коливань.

Ці вирази – параметрична форма рівняння траєкторії, вздовж якої рухається точка, що бере участь в обох коливаннях. Щоб отримати рівняння траєкторії у звичайному вигляді, треба виключити з цих рівнянь параметр. Проведемо наступні перетворення:

, ,

;

,

.

В результаті отримаємо

.

Це рівняння еліпса, осі якого повер­нуті відносно координатних осейOXіOY. Орієнтація еліпса і величини його півосей залежать від амплітудOAіOBі різниці фаз.

Розглянемо частинні випадки.

1).

Тоді ;

звідси .

Результуюче коливання є гармонічним вздовж прямої з частотоюі амплітудою(рис. 32). Пряма утворює з віссюXкут.

2). ,

Уцьому випадку

;

і

.

Результуючий рух – це гармонічне коливання вздовж прямої (рис. 33).

3).

В результаті .

Це рівняння еліпса, осі якого збігаються з осями координат, а його півосі дорівнюють відповідним амплітудам (рис. 34).

Якщо А=В,то еліпс вироджується в коло. Випадки

і

відрізняються напрямком руху по еліпсу чи колу.

Якщо частоти взаємно перпендикулярних коливань, що додаються, різні, то замкнена траєкторія результуючого коливання досить складна.

Замкнені траєкторії, що кресляться точкою, яка здійснює одночасно два взаємно перпендикулярні коливання, назива­ються фігурами Ліссажу. Форма цих кривих залежить від співвідношення амплітуд, частот і різниці фаз коливань, що додаються (рис. 35).

§17. Диференціальне рівняння згасаючих коливань і його розв’язання

Усі реальні коливальні системи є дисипативними. Енергія механічних коли­вань такої системи поступово витрачається на роботу проти сил опору, тому вільні коливання завжди згасаючі - їх амплітуда поступово зменшується.

Для пружинного маятника масою m, що здійснює малі коливання під дією пружної сили, сила опору пропорційна до швидкості, тобто

, ,

де – коефіцієнт опору.

Другий закон Ньютона для згасаючих коливань має наступний вигляд:

,

Введемо позначення

, ,

де – коефіцієнт згасання, а– власна частота з якою здійснювались би вільні коливання за відсутності опору середовища.

Тоді другий закон Ньютона можна записати у вигляді

.

Для розв’язання цього рівняння введемо нову змінну u, яка зв’язана зxспіввідношенням. Звідси

,

.

Підставивши ці значення ів рівняння другого закону Ньютона для зга­саючих коливань і скорочуючи всі доданки на множник, отримуємо

.

Нехай опір середовища малий і . Тоді можна ввести позначення

.

В результаті отримуємо рівняння

,

розв’язок якого має такий вигляд

,

де і– сталі, які визначаємо з початкових умов. Отже,

,

де - амплітуда загасаючих коливань, а- початкова амплітуда. Амплітуда згасаючих коливань зменшується з плином часу і тим скоріше, чим більший коефіцієнт опору і чим менша масаколивного тіла.

Величина називається власною циклічною частотою коливань дисипативної системи. Графік залежностіxвід часу наведений на рис. 36.

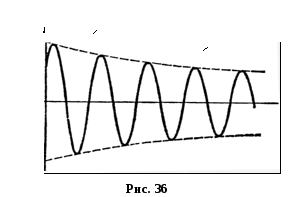
Згасаючі коливання – неперіодичні коливання, бо в них ніколи не повторюються, наприклад, максимальні значення змі­щення, швидкості і прискорення. Однак при згасаючих коливаннях величина xперетворюється в нуль, змінюючись в один і той самий бік, а також досягає максимальних і мінімальних значень через однакові проміжки часу:

.

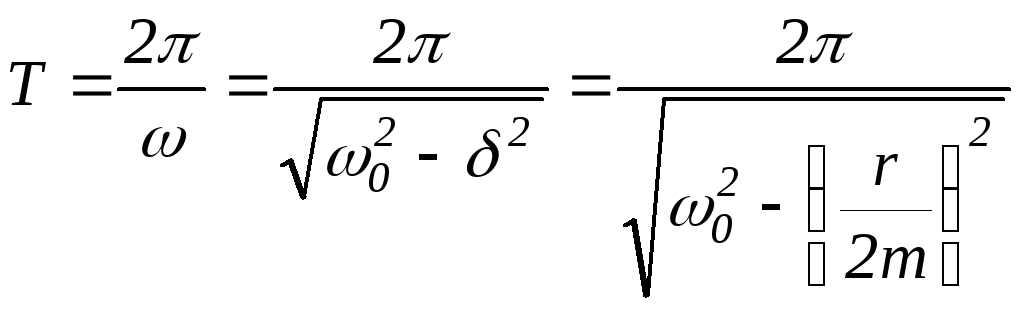Величину Tтому називають періо­дом згасаючих коливань.

Якщо і– амплітуди двох послідовних коливань, що йдуть одне за одним через проміжок часуT, то відношення

називається декрементом згасання, а його натуральний логарифм

æ

– логарифмічний декремент згасання.

Позначимо проміжок часу, протягом якого амплітуда коливань зменшується вeразів. Тоді

Звідси

, або .

Коефіцієнт згасання є фізична величина, обернена до проміжку часу, протягом якого амплітуда зменшується вeразів. Часназивається часом релаксації.

Нехай N– кількість коливань, після яких амплітуда коливань зменшується вeразів. Тоді

, æ.

Логарифмічний декремент згасання æ є фізична величина, обернена до кількос­ті коливаньN, після закінчення яких амплітуда зменшується вeразів.

Добротністю коливальної системиназивається величина, яка дорівнює добуткуна відношення енергіїколивальної системи в довільний момент часуtдо зменшення цієї енергії за проміжок часу відtдоt+T:

.

Оскільки енергія пропорційна до квадрата амплітуди коливань, то

.

При малих значеннях æ(æ<<1)

і

.

Тут враховано, що при æ<<1і умовний періодТзгасаючих коливань практично дорівнює періодувільних коливань.