§18. Диференціальне рівняння вимушених коливань і його розв’язання. Резонанс

Розглянемо коливання, що їх здійснює система, якщо на неї, крім пружної сили і сили опору, діє ще додаткова періодична силаF, яку називатимемовимушуючою силоюі яка змінюється за гармонічним законом

.

Диференціальне рівняння вимушених коливань, що відбувається вздовж осі OX, має такий вигляд:

,

де ,,.

Загальний розв’язок диференціального рівняння вимушених коливань дорівнює сумі загального розв’язку відповідного однорідного рівняння

,

де і частинного розв’язкунеоднорідного рівняння. Доданоквідіграє помітну роль лише на початковій стадії процесу виникнення коливань (рис. 37). З часом внаслідок експоненціального множникароль доданказменшується, амплітуда вимушених коливань зростає, доки не досягне значенняA.

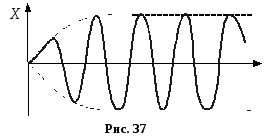
Отже, усталені вимушені коливання системи, які виникають під дією сили F, також є гармонічними, тобто

,

причому їх циклічна частота дорівнює циклічній частоті вимушуючої сили.

Задача полягає в знаходженні амплітуди Aі початкової фази.

Знайдемо і :

,

.

Підставивши вирази для ,, іxу диференціальне рівняння вимушених коливань, отримаємо

.

З цього рівняння видно, що амплі­туда Aі фазаповинні мати такі значен­ня, щоб гармонічне коливаннядорівнювало сумі трьох гармонічних коливань, що знаходяться в лівій частині рівняння.

Введемо позначення

, , , .

Тоді

.

Щоб додати ці коливання, використаємо метод векторних діаграм. Відкладемо під кутом до осіОХ за годинниковою стрілкою вектор, потім під кутомвідносно векторапроти годинникової стрілки побудуємо векторі вектор, який повернутий на кутвідносно вектора. Додавши три вектори,,, отримаємо вектор(рис. 38).

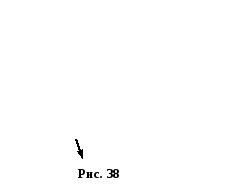
З рис. 38видно, що

,

і, відповідно,

.

Звідси

.

Амплітуда усталених вимушених коливань прямо пропорційна до амплітуди вимушуючої сили , обернено пропорційна до масиmсистеми і зменшується із збільшенням коефіцієнта загасання.

Із рис. 38можна отримати значення- зсув мас між зміщенням і вимушуючою силою:

.

Якщо ,mісталі, то амплітуда усталених вимушених коливань залежить тільки від співвідношення між циклічними частотами вимушуючої силиі вільних коливань системи.

Розглянемо залежність амплітуди Aвимушених коливань від частотиі побудуємо криві(рис. 39) при різних значеннях коефіцієнта згасання. Чим менше, тим вище і правіше лежить максимум кривої. Якщо, то

.

в такому разі коливання не здійснюються, а відхилення називається статичною амплітудою. Привсі криві асиптотично прямують до нуля. Якщо загасання немає, то амплітуда коливаньзростає із зростанням циклічної частотивимушуючої сили і пристає нескінченно великою.

Якщо є згасання , то амплітуда досягає максимального значення, коли вираз, що є в знаменнику співвідношення дляA, досягає мінімуму. Це відбувається, коли

.

Виконуючи диференціювання, от­римуємо

.

Це рівняння має два розв’язки: ,. Розв’язоквідповідає максимуму знаменника виразу дляA. Із інших двох розв’язків лише додатний має фізичний сенс.

Отже, резонансна частота – частота, при якій амплітуда A коливань досягає максимального значення, – має такий вигляд.

.

Явище різкого зростання амплітуди вимушених коливань при наближенні частоти вимушуючої сили до частоти називаєтьсярезонансом.

Для консервативної системи , а для дисипативної системитрохи менша від власної частотисистеми.

Підставивши у вираз для амплітудиA, отримаємо вираз для амплітуди при резонансі:

.

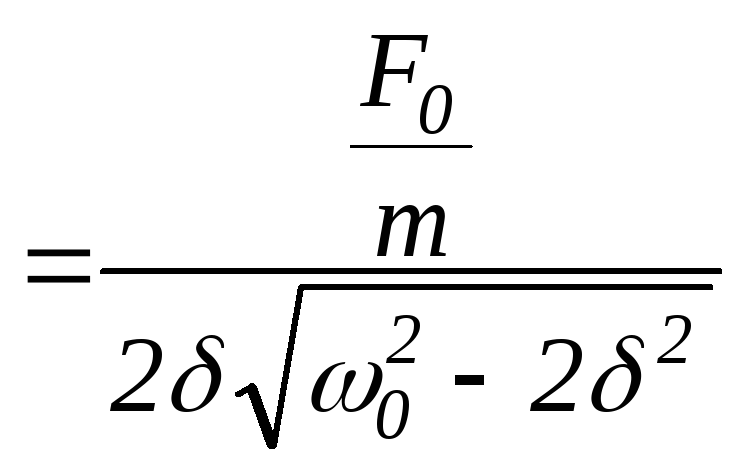При малому згасанні амплітуда при резонансі приблизно дорівнює

,

де – добротність коливної системи. Отже, добротність характеризує резонансні властивості коливної системи: чим більше значення, тим більше.

З виразу видно, що у випадкузміщення коливної системи і вимушуюча сила мають однакові фази; у всіх інших випадках. Залежністьвідпри різних значенняхнаведена на рис. 40. При, принезалежно від значення, тобто вимушуюча сила випереджує за фазою зміщення на. При подальшому збільшеннізсув фаз зростає і при>>, тобто фаза зміщень коливальної системи майже протилежна до фази зовнішньої вимушуючої сили.