4.2. Момент силы относительно полюса (центра, точки)

Момент силы относительно полюса характеризует меру вращательной способности силы, приложенной к телу, имеющему неподвижную точку. Так как он должен указывать направление оси возможного поворота, то это должен быть вектор.

О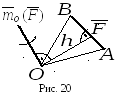пределение:Моментом силы относительно полюса называется вектор (рис. 20), приложенный в полюсе, направленный перпендикулярно плоскости, проходящей через полюс и силу в ту сторону, откуда видно, что сила стремится вращать тело вокруг полюса против часовой стрелки, и равный по величине произведению величины силы на плечо. Плечом называется длина перпендикуляра, опущенного из полюса на линию действия силы.

Обозначение: . Читается так: момент силыотносительно полюса. Величина момента. Так как плечоможно рассматривать как высоту треугольника, о можно сказать, что величина момента силы относительно полюса равна удвоенной площади треугольника

.

Заметим, что эта "площадь" будет измеряться в ньютоно-метрах, так как основание треугольника–сила, а высота–длина.

Основные свойства момента силы относительно полюса

1. Момент силы относительно полюса не изменяется, если силу переносить вдоль ее линии действия.

2. Если линия действия силы проходит через полюс, то момент силы относительно полюса равен нулю.

3. Сумма моментов двух прямопротивоположных сил относительно одного и того же полюса равна нулю.

Эти свойства легко проверяются.

4.3. Момент силы относительно полюса как векторное произведение

Определим положение точки приложения силывектором, который называетсярадиус-вектором точки приложения силы(рис. 21).

Тогда справедлива теорема.

Теорема.Момент силы относительно полюса равен векторному произведению радиус-вектора точки приложения силы на вектор силы, то есть

.

Доказательство:

Такое представление момента силы относительно полюса легко проверяется. Для этого покажем, что векторы, стоящие в правой и левой частях этого равенства, равны по величине и одинаково направлены. В самом деле, модуль векторного произведения равен

,

где —плечо силы. По определению векторнаправлен перпендикулярно плоскости, содержащей векторыи(плоскости), в ту сторону, откуда кратчайший поворот векторак направлению векторапредставляется происходящим против часовой стрелки, то есть так же, как вектор. Следовательно, векторыисовпадают и по величине и по направлению.

4.4 Связь между моментами силы относительно полюса и оси

Теорема.Проекция момента силы относительно полюса на ось,проходящую через этотполюс, равна моменту силы относительно оси :

.

Доказательство:

Для доказательства вычислим левую и правую части предполагаемого равенства и убедимся, что результаты вычислений совпадают (рис. 22).

Момент силы относительно полюсаперпендикулярен плоскости треугольникаи по величине. Обозначим угол междуи осьючерез. Тогда проекцияна ось:

Проведем через полюс плоскость, перпендикулярную оси и вічислим момент силіотносительно оси:

(рассматривается случай, когда стремится повернуть плоскость вокруг оси против хода часовой стрелки).

Воспользуемся простым положением элементарной геометрии: площадь проекции плоской фигуры () на некоторую плоскость () равна площади проектируемой фигуры (), умноженной на косинус угла между плоскостью проекции и плоскостью проектируемой фигуры. Угол между двумя плоскостями – это угол между перпендикулярами к этим плоскостям в их общей точке, то есть угол. Тогда. Следовательно

.