
- •Введение
- •Основные понятия и аксиомы статики
- •1.1 Сила и система сил
- •1.3. Аксиомы статики
- •Связи и их реакции
- •4. Связь с неподвижным центром вращения (сферический шарнир)
- •5. Опорный стержень
- •3. Система сходящихся сил
- •3.1 Теорема о равновесии тела под действием сходящейся системы сил(векторные условия равновесия)
- •Аналитические условия равновесия тела, загруженного сходящейся системой сил
- •Теорема о трех непараллельных силах (правило трех сил)
- •4. Момент силы
- •4.1. Момент силы относительно оси
- •4.2. Момент силы относительно полюса (центра, точки)
- •4.3. Момент силы относительно полюса как векторное произведение
- •4.4 Связь между моментами силы относительно полюса и оси
- •4.5. Главный момент системы сил
- •4.6. Зависимость между главными моментами системы сил относительно двух полюсов
- •4.7. Теорема Вариньона (частный случай)
- •Элементарные операции статики. Эквивалентные системы сил
- •Элементарные операции статики
- •5.2. Эквивалентные преобразования. Эквивалентные системы сил. Равнодействующая
- •5.3. Обобщенная теорема Вариньона
- •6. Условия равновесия. Условия равновесия в общем и частных случаях
- •6.1. Основная лемма статики
- •6.2. Основная теорема статики (общие условия равновесия системы сил)
- •6.3. Аналитические условия равновесия произвольной системы сил (шесть уравнений статики абсолютно твердого тела)
- •6.4 Частные случаи аналитических условий равновесия
- •7. Общий признак эквивалентности двух систем сил (критерий эквивалентности)
- •8. Теория пар сил
- •8.1. Момент пары сил
- •8.2. Признак эквивалентности двух пар сил
- •8.3. Следствия из признака эквивалентности пар
- •8.4. Теорема о "сложении" пар
- •9. Приведение системы сил к заданному центру
- •9.1. Лемма о параллельном переносе силы
- •9.2. Теорема Пуансо (о приведении системы сил к заданному центру)
- •9.3. Частные случаи приведения системы сил к заданному центру
- •9.4. Инварианты системы сил
- •10. Центр параллельных сил. Центр тяжести
- •10.1. Центр системы параллельных сил
- •10.2. Центр тяжести твердого тела
- •2. Центр тяжести плоской фигуры
- •3. Центр тяжести линии
- •10.3. Статические моменты
- •10.4. Центры тяжести симметричных тел
- •10.5. Основные способы определения центра тяжести
- •11. Трение скольжения
- •11.1. Сила трения и коэффициент трения
- •11.2. Угол трения. Конус трения
9.4. Инварианты системы сил
Определение. Инвариантами системы сил называются величины, не зависящие от выбора центра приведения, то есть величины, которые остаются неизменными при преобразовании данной системы сил в другую, ей эквивалентную.
1-й инвариант –
главный вектор системы сил ![]() .
.
2-й
инвариант – скалярное произведение
главного вектора на главный момент![]()
Доказательство.
Пусть
известно скалярное произведение
![]() для системы сил, приведенной к полюсу
для системы сил, приведенной к полюсу![]() .
Вычислим то же произведение
.
Вычислим то же произведение![]() для системы сил, приведенной к другому
полюсу
для системы сил, приведенной к другому
полюсу![]() .
Главный вектор не зависит от выбора
полюса; для нового центра приведения
главный момент будет иным:
.
Главный вектор не зависит от выбора
полюса; для нового центра приведения
главный момент будет иным:
![]()
(по теореме о зависимости между главными моментами системы сил относительно двух полюсов).
Тогда:
![]() ,
,
так как по правилам вычисления смешанного произведения
![]()
( векторное произведение параллельных векторов равно нулю).
Таким
образом
![]() .
.
10. Центр параллельных сил. Центр тяжести
10.1. Центр системы параллельных сил
Система
параллельных сил в общем случае приводится
к силе и паре, причем векторы силы и пары
перпендикулярны. Тогда, если
![]() ,
то система приводится к равнодействующей.
,
то система приводится к равнодействующей.
 Рассмотрим
систему параллельных сил
Рассмотрим
систему параллельных сил![]() ,
приложенных соответственно в точках
,
приложенных соответственно в точках![]() твердого тела (рис. 46).
твердого тела (рис. 46).
Определение. Центром системы параллельных сил называется точка приложения равнодействующей системы параллельных сил, которая остается неизменной при любых поворотах всех сил системы вокруг их точек приложения на один и тот же угол.
Центр
параллельных сил существует, если
главный вектор системы сил не равен
нулю
![]() .
.
Пусть
![]() ,
тогда
,
тогда![]() ,
где
,
где![]() – равнодействующая. Введем единичный
вектор
– равнодействующая. Введем единичный
вектор![]() (
(![]() ),
направленный параллельно линиям действия
сил. Тогда любая сила
),
направленный параллельно линиям действия
сил. Тогда любая сила![]() ,
где
,
где![]() ,
если направление силы
,
если направление силы![]() и вектора
и вектора![]() совпадают, и
совпадают, и![]() ,
если
,
если![]() и
и![]() направлены противоположно друг другу.
Пусть равнодействующая
направлены противоположно друг другу.
Пусть равнодействующая![]() приложена в точке
приложена в точке![]() ,
радиус-вектор которой
,
радиус-вектор которой![]() .
По обобщенной теореме Вариньона момент
равнодействующей относительно полюса
.
По обобщенной теореме Вариньона момент
равнодействующей относительно полюса![]() равен сумме моментов всех сил системы
относительно того же полюса:
равен сумме моментов всех сил системы
относительно того же полюса:
![]() ,
,
или ![]() .
.
Тогда ![]() .
.
Преобразуем полученное выражение:
![]() ,
,
![]() ,
,
![]() .
.
Выражение
в круглых скобках представляет собой
некоторый вектор, который обозначим
![]() ,
тогда:
,
тогда:
![]() .
.
Но
![]() ,
а полученное равенство не должно зависеть
от угла поворота сил вокруг их точек
приложения, то есть угол между векторами
может быть любым. Поэтому векторное
произведение
,
а полученное равенство не должно зависеть
от угла поворота сил вокруг их точек
приложения, то есть угол между векторами
может быть любым. Поэтому векторное
произведение![]() ,
когда
,
когда
![]() ,
,
откуда получаем выражение для радиус-вектора центра параллельных сил
 .
.
Проектируя полученное равенство на оси координат, получим выражения длякоординат центра параллельных сил
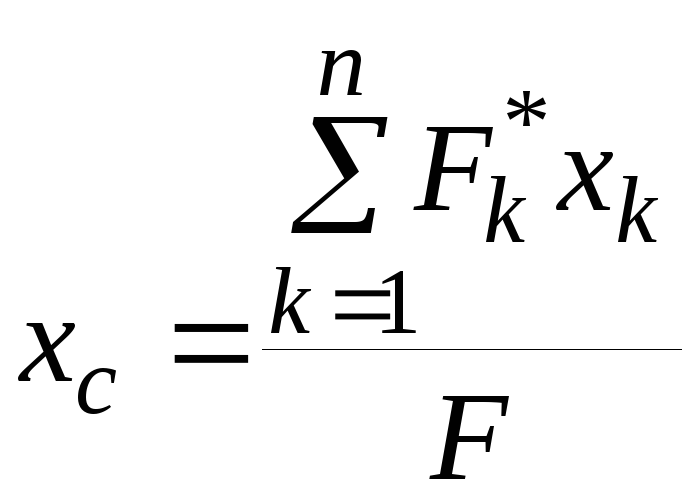 ,
, 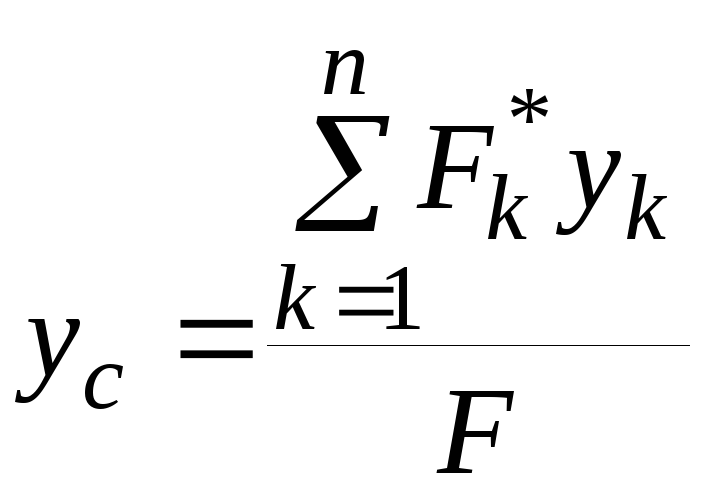 ,
,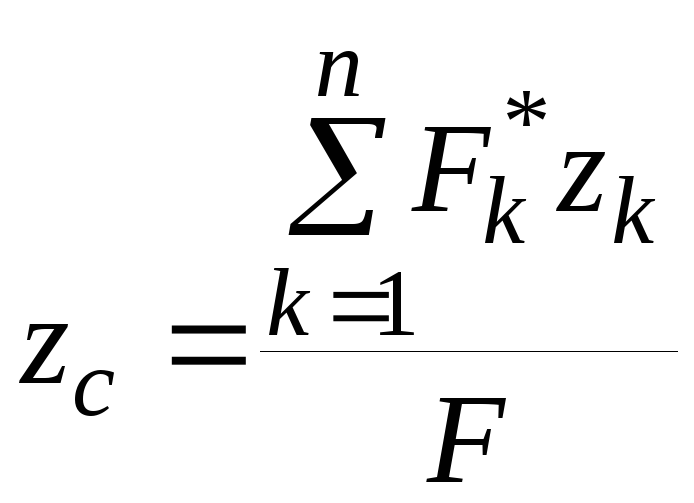 ,
,
где
![]() – координаты центра параллельных сил,
а
– координаты центра параллельных сил,
а![]() – координаты точки приложения
– координаты точки приложения![]() .
.
10.2. Центр тяжести твердого тела
Силы притяжения отдельных частиц тела к Земле направлены приблизительно к центру Земли. Так как размеры рассматриваемых тел малы по сравнению с радиусом Земли, то эти силы можно считать параллельными. Равнодействующая этих параллельных сил, равная их сумме, есть вес тела.
Определение. Центром тяжести твердого тела называется центр параллельных сил тяжести частиц, слагающих тело. Иными словами, центр тяжести – это такая точка приложения равнодействующей сил тяжести частиц тела, которая остаётся неизменной при любых поворотах тела.
Таким образом, для определения положения центра тяжести можно использовать формулы для координат центра параллельных сил.
О бозначим
силы веса отдельных частиц тела
бозначим
силы веса отдельных частиц тела![]() ,
вес тела
,
вес тела![]() ,
координаты его центра тяжести
,
координаты его центра тяжести![]() ,
а координаты любой частицы твердого
тела
,
а координаты любой частицы твердого
тела![]() (рис. 47).
(рис. 47).
Тогда формулы для определения координат центра тяжести принимают вид:
 ,
,  ,
,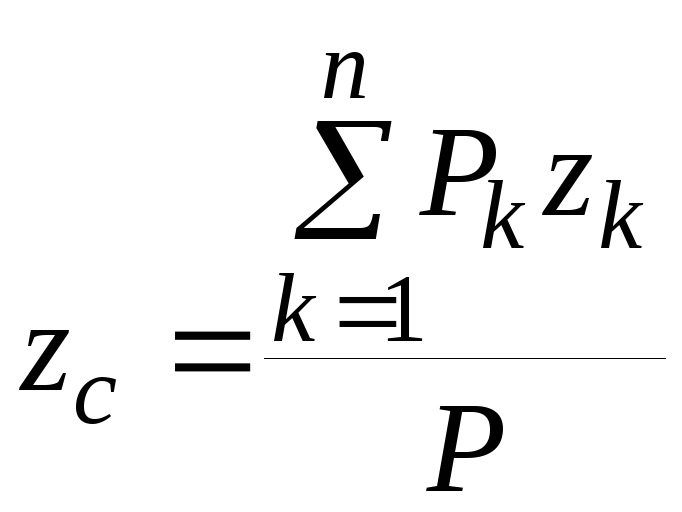 .
.
Определим положение центра тяжести однородных тел.
Центр тяжести объема
Вес
однородного тела определяется по формуле
![]() ,
где
,
где![]() – объём тела,
– объём тела,![]() –вес единицы объема. Аналогично, вес
каждой частицы
–вес единицы объема. Аналогично, вес
каждой частицы![]() ,
где
,
где![]() – объем
– объем![]() – ой частицы тела. Обозначим
– ой частицы тела. Обозначим![]() координаты центра тяжести этой частицы.
Тогда
координаты центра тяжести этой частицы.
Тогда
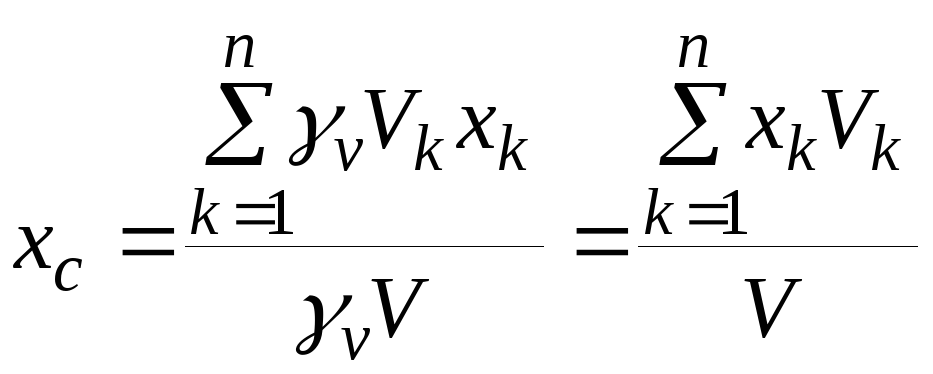 ,
,  ,
, .
.
