Сложение чисел

В основу сложения чисел в двоично-десятичной СС положено сложение двоичных

чисел с коррекцией результата по каждой тетраде. На рис. 9 показан алгоритм алг. 5

с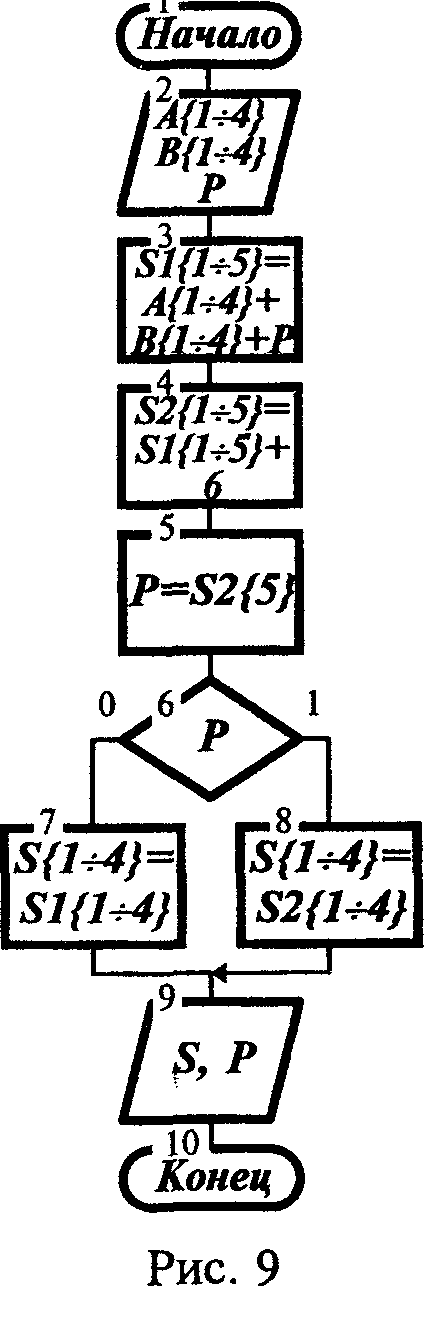ложения десятичных цифр, которые изображены тетрадами в двоично-кодированной СС с весами8, 4, 2, 1. Блок 2 вводит слагаемые тетрады а{1-4) и Ь{1-4},

двоичные разряды которых пронумерованы, начиная с младшего разряда, а также перенос

р из предыдущей тетрады. Блок 3 складывает тетрады по алгоритму алг. 3 сложения

двоичных чисел с учетом переноса р и формирует при этом 5-разрядное двоичное число s1, которое при s1<10 совпадает в четырех младших разрядах с тетрадой результата. В случае s1>10 в блоке 4 выполняется перевод числа s1 в двоично-десятичную СС, с получением числа s2=^:s1+6, которое содержит тетраду результата s и перенос р в следующую тетраду. Блок 5 присваивает переносу р его значение, которое было вычислено в s2. Блок 6 в зависимости от переноса р предписывает выполнение или блока 7, или блока 8, которые присваивают тетраде результата s четыре младших разряда соответственно чисел s1 или s2. Блок 9 выводит результаты s и р. Алгоритм закончен.

Сложение многотетрадных чисел выполняется последовательно обработкой цифр, т. е. по алгоритму алг. 3, который изображен на рис. 6, или по алгоритму ускоренного сложения, в котором подобно алгоритму алг. 4 сложения двоичных чисел (рис. 8) (см. билет 27 Сложение чисел) цифры (тетрады) прибавляются одновременно без учета межтетрадных переносов, а переносы составляют число, сложение с которым выполняется в следующей итерации.

Рассмотрим пример сложения чисел в двоично-десятичной СС.

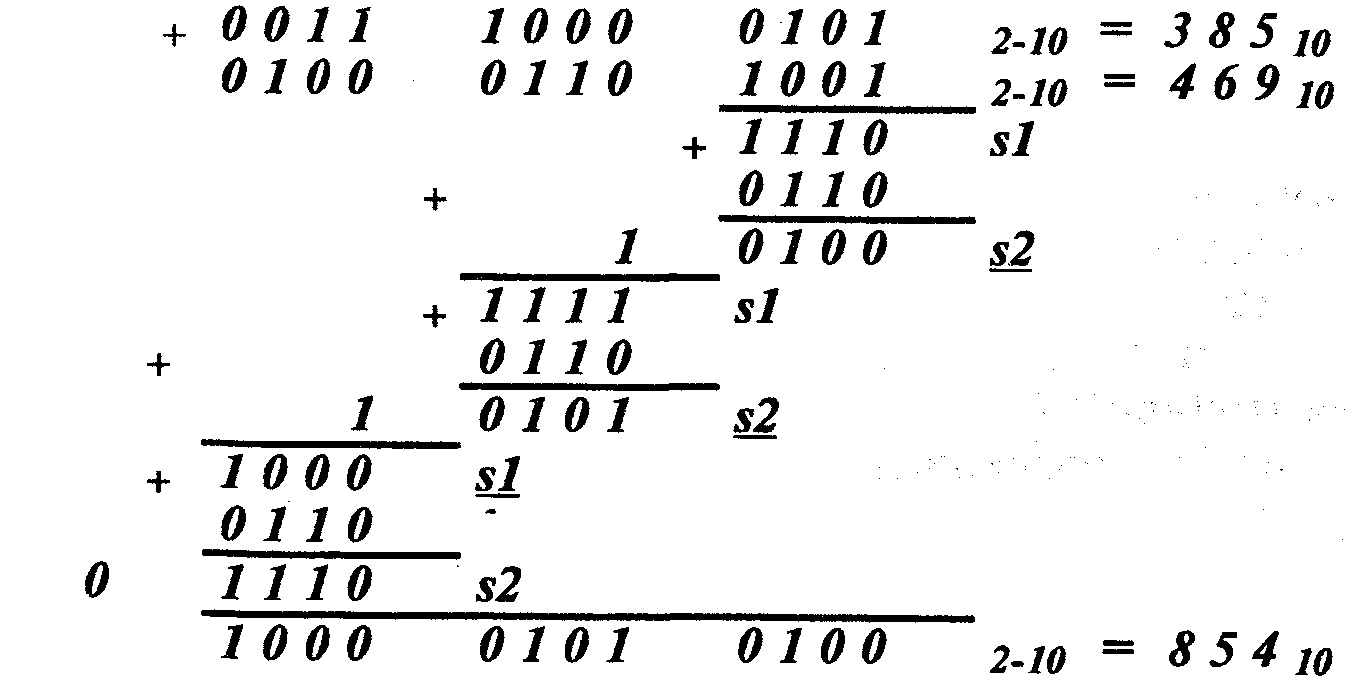
У

Таблица 5

Цифра множимого	Значения суммы	Перенос
0	S=S+0	0
1	S=S+A	0
2	S=S+2A	0
3	S=S+2A+A	0
4	S=S+4A	0
5	S=S+4A+A	0
6	S=S-4A	1
7	S=S-2A-A	1
8	S=S-2A	1
9	S=S-A	1

множение чисел в двоично-десятичной СС сводится к последовательному сложению частных произведений, получаемых при умножении множимого на очередную цифру множителя.

Умножение десятичных чисел выполняется по методу ускорения, в котором все операции сводятся к последовательности операций сложения или вычитания в обратном или дополнительном кодах. В табл. 5 для каждого значения цифры множителя показаны операции над накапливаемой суммой S и множимым А, а также значение адресуемого в следующую тетраду переноса.

Рассмотренные способы умножения выполняют операцию над числами в естественной форме представления.

делениевыполняется аналогичноумножению (только суммы другие)

№ 32. Контроль по модулю арифметических операций.

Функциональное диагностирование использует структурную избыточность и реализуется средствами и методами аппаратного контроля

Среди них семантический контроль, называемый также контролем по запрещенным значениям. Он использует естественную информационную избыточность результата, который не может принимать ряд значений, относящихся по этой причине к запрещенным значениям. Формирование запрещенных значений указывает на неправильную работу устройства и в семантическом контроле используется как признак неисправности. Например, при возведении в квадрат двухразрядных чисел правильный результат не может принимать значений 2, 3, 5, 8, 10-15.

Иной подход основывается на проверке результата выполнением обратной операции. Такой контроль используется, если обратная операция существенно проще прямой. Например, операция деления может быть проверена выполнением обратной для нее операции умножения.

Универсальный характер имеет классический подход к контролю арифметических операций и реализующих их устройств. В нем для каждого числа - операндов и результата - определяется его контрольный код. Над контрольными кодами операндов выполняется операция, аналогичная операции, осуществляемой над самими операндами. Получении контрольный результат сравнивается с контрольным кодом результата. Результат сравнения является сигналом контроля, позволяющим судить о правильности выполнения операции.

Наибольшее распространение среди реализующих классический подход методов имеет контроль арифметических операций по модулю.

Модулем является целое число, используемое для формирования контрольных кодов чисел. Операция вычисления контрольного кода КХ некоторого числа Х по модулю т описывается выражением Xmodm.

Различают контроль по числовому и цифровому модулям. При контроле по числовому модулю контрольный код числа определяется как остаток от деления этого числа на модуль, а при контроле по цифровому модулю - как остаток от деления на модуль суммы цифр этого числа.

Контроль по числовому модулю т основан на разбиений всего числового пространства на т классов эквивалентности, которые характеризуются разными значениями остатка от деления чисел на модуль т. Например, по модулю т=3 все числа разбиваются на 3 класса эквивалентности, принимающие соответственно значения остатка 0, 1 и 2. Ошибки обнаруживаются за счет отнесения искаженного результата к другому классу эквивалентности, чем правильный результат.

Если неправильный и правильный результаты оказались в одном и том же классе эквивалентности, то контроль не может различить эти результаты, что ведет к необнаружению ошибки. Очевидно, что для произвольной ошибки вероятность Р_НО ее необнаружения определяется по формуле Р_НО=1/т, а вероятность р₀ обнаружения ошибки Ро=1-1/т.

Величина ро для практического использования уточняется путем ее расчета для характерных, наиболее часто встречающихся ошибок. При этом ее значение растет. Например, контроль по любому модулю т одиночных ошибок (искажение одного разряда результата) выполняется с р₀ =1.

Для контроля по числовому модулю т выполняются следующие контрольные соотношения:

(Amodm +Bmodm)modm =Cmodm,

(Amodm •Bmodm)modm = Vmodm, где С=А+В, V=AB, или

KA+KB=KC,

KAKB=KV, где KA=-Amodm,

KB=Bmodm,

KC=Cmodm,

KV=Vmodm,

используемые соответственно для проверки операций сложения и умножения. Контроль этих операций по цифровому модулю может привести к реализации более сложных контрольных соотношений, но вместе с тем характеризуется простым способом вычисления контрольных кодов.

Практический интерес представляют модули, сочетающие простоту контрольных соотношений и способов вычисления контрольных кодов, поскольку одновременно являются и числовыми, и цифровыми модулями. Это модули вида m=q-l, где q - основание СС. Легко показать, что вес каждой цифры СС с основанием q делится на m с остатком 1. Из этого следует одинаковая делимость на т числа и суммы его цифр, т. е. принадлежность т к числовым и цифровым модулям. Контрольные коды представляют собой цифру СС с основанием q и имеют природу обратного кода с двумя представлениями нуля: +0 = 0, -0 = q - 1.

Рассмотрим примеры проверки операций сложения и умножения десятичных чисел, для которых q=30, m=9.

1. 835+116=951,

835mod9=(8+3+5)mod9=16mod9=(l+6)mod9=7.

116mod9=(l+l+6)mod9=8,

951mod9=(9+5+1)mod9=15mod9=(1+5)mod9=6.

В данном примере контрольные коды чисел 835, 116, 951 составляют соответственно 7, 8, и 6, а контрольное соотношение имеет вид:

(7+8)mod9=15mod9=6.

2) 12*13=156,

12mod9=(1+2)mod9=3,

13mod9=(1+3)mod9=4,

156mod9=(1+5+6)mod9=12mod9=(1+2)mod9=3.

Контрольные коды чисел 12, 13, 156 составляют 3, 4 и 3 соответственно, а контрольное соотношение имеет вид:

(3* 4)mod9=12mod9=(1+2)mod9=3.

Для двоичной СС в форме двоично-кодированных СС с основанием q=2^l, где l=2, 3, ... , модули имеют вид m=2^l-l.

Контрольные коды содержат l двоичных разрядов и формируются путем сложения в обратном коде l-разрядных кодов цифр, выделенных в обратном коде двоичного числа. Операция вычисления контрольных кодов называется сверткой по модулю.

Расcмотрим примеры проверки операций сложения и умножения двоичных чисел по модулям вида т=2^l-1 для т=3 и т=7.

1.01011об +0.01110об =1.11001об,

1.01011об* 0.01110об =1.11011100111об,

(1.01011об)mod3=(10₂+10₂+11₂)mod3=01₂,

(0.01110об)mod3=(00₂+11₂+10₂)mod3=10₂,

(1.11001об)mod3=(11₂+10₂+01₂)mod3=11₂,

(1.11011100111об)mod3=(11₂+10₂+11₂+10₂+01₂+11₂)mod3=10₂.

Контрольные коды чисел

1.01011об =-20₁₀

0.01110об =14₁₀

1.11001 об =-6₁₀

1.11011100111об =-28₁₀

принимают для т=3, l=2 значения соответственно 01₂, 10₂, 11₂ и 10₂, а контрольные соотношения имеют вид:

(01₂+10₂)mod3=11₂,

(O1₂ 10₂)mod3=10₂.

Контрольные коды тех же чисел для т=7, 1=3 и контрольные соотношения для операций сложения и умножения таковы:

(1.01011об)mod7=(101₂+O11₂)mod7=OO1₂,

(0.01110об)mod7=(001₂+110₂)mod7=111₂,

(1.11001об)mod7=(111₂+001₂)mod7=001₂,

(1.11011100111об)mod7=(111₂+011₂+100₂+111₂)mod7=111₂,

(001₂+111₂)mod7=001₂,

(001₂111₂)mod7=111₂.

При определении контрольных кодов разрядность двоичных чисел должна быть кратна l, что достигается наращиванием (при необходимости) количества знаковых разрядов.

Проверка правильности вычисления арифметических выражений, составленных из операций сложения (вычитания) и умножения, выполняется по контрольным соотношениям, получаемым выполнением операции mod над выражениями в формулах основных преобразований.

В качестве примера, рассмотрим контроль операции целочисленного деления. Для этого обратимся к описанной в подразделе 3.3 формуле, связывающей операнды и результаты выполнения этой операции:

A=BC+D,

где А - делимое; В - делитель, С - частное, D - остаток (|D|<B ).

Тогда контрольные соотношения получаются следующим образом:

Amodm =(B- C+D)modm =((B- C)modm +Dmodm)modm ==(Bmodm • Cmodm +Dmodm)modm или KA=KBKC+KD.

Приведем пример контроля операции деления по полученному контрольному соотношению для т=3 и следующих чисел:

А=152₁₀=10011000₂,

В=13₁₀=1101₂,

С=11₁₀=1011₂,

D=9₁₀=1001₂,

KA=(10011000₂)mod3=(10₂+01₂+10₂+00₂)mod3=10₂,

KB=(1101₂)mod3=(11₂+01₂)mod3=01₂,

KC=(1011₂)modЗ=^::(10₂+11₂)modЗ=10₂,

KD=(1001₂)mod3=11₂,

10₂=(01₂10₂+11₂)mod3.

Рассмотрим контроль по модулю арифметических операций с плавающей точкой. Он имеет особенности, которые связаны с различиями между формами представления чисел и существенно отличают его от описанного контроля операций над числами в естественной форме представления. Во-первых, контроль выполняется отдельно для порядков и мантисс. Причем порядки являются целыми числами с фиксированной точкой и описанный выше контроль по модулю полностью распространяется на проверку операций над порядками. Во-вторых, операции над мантиссами выполняются с сохранением единых форматов для операндов и результата операции, т. е. с вычислением по n-разрядным операндам округленного n-разрядного результата. Для это целесообразно использовать методы сокращенного выполнения операций, что ставит задачу контроля правильности выполнения сокращенных операций.

Сокращение вычислений в операциях связано с выполнением операции умножения, присутствующей во всех арифметических операциях с плавающей точкой и удваивает разрядность полного результата в сравнении с разрядностью сомножителей. Поэтому рассмотрим контроль по модулю операции сокращенного умножения.

Контрольное соотношение для проверки округленного результата умножения складывается с использованием разбиения старшей части матрицы на фрагменты.

Фрагмент Vi - часть матрицы, которая определяется произведением

Vi=AiBi signVi,

где Аi, и Bi, - образующие фрагмента Vi,

Ai {Bi) - множимое (множитель) или его часть,

signVi - знак фрагмента Vi, signVi,=+1, если большинство конъюнкций расположено в старшей части матрицы, и signVi=-1 в противоположном случае.

Сумма фрагментов, составляющих старшую часть матрицы, определяет усеченное произведение:

где n_k - количество этих фрагментов.

Округленный результат равен

что с переходом к контрольным кодам чисел определяет контрольное соотношение:

Минимальное количество слагаемых в контрольном соотношении достигается при п^ = k+1 в том и только в том случае, если все фрагменты являются индексируемыми, т. е. фрагменту в качестве индекса ставится в соответствие номер строки матрицы, которая содержит в составе фрагмента только один граничный элемент (граничные элементы - конъюнкции, которые прилегают к линии раздела матрицы на младшую и старшую части). На рис. 20 показано разбиение матрицы на индексируемые фрагменты для n=16, k=12.

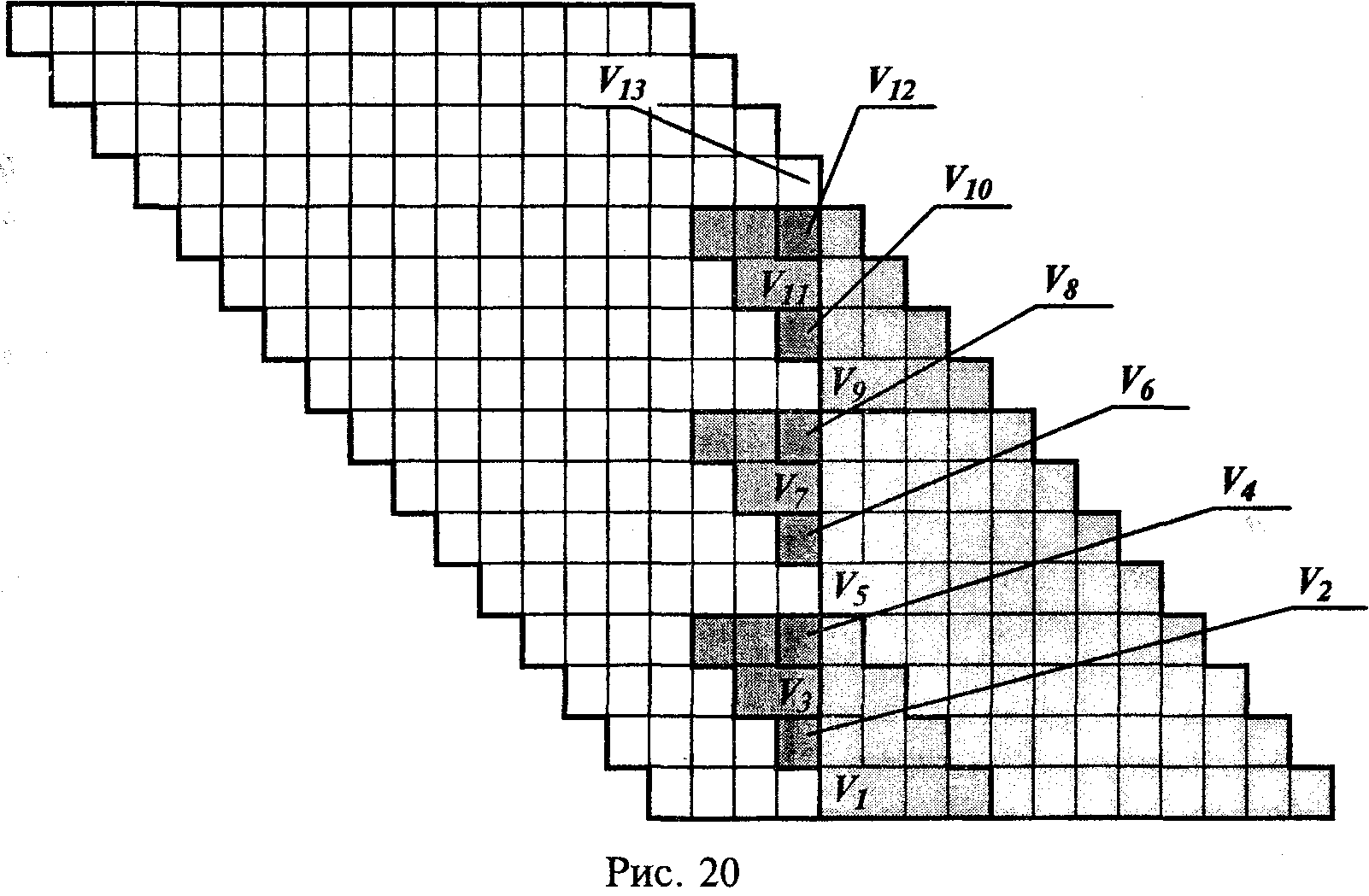
Фрагменты могут быть внешними один по отношению к другому, как v₁ и Vs или вложенными один в другой, например, v₃ в v₁, центрально-симметричными при Ai=Bj как V₅, V₇ или составлять пару взаимосимметричных фрагментов Vi , Vj, если Ai=Bj и Bi=Aj, который записывается как Vi=Vj* или Vj = Vi*, например V1=V9*, V3=V11*. Количество разрядов составляющей Аi, или Вi, фрагмента Vj является размером фрагмента по этой составляющей соответственно L_Ai или L_Bi, a при L_Ai = L_Bi, - размером Z, фрагмента Vj, например, L₅=8, L₉=4, L₁₁=2.

Приведем описание фрагментов разбиения:

V₁= - A{58}B{1316}2^-24, V₂=A{5}B{15}2^-20,

V₃= A{56}B{1314}2^-20, V₄=A{7}B{13}2^-20,

V₅= - A{916}B{916}2^-32, V₆=A{9}B{11}2^-20,

V₇= A{910}B{910}2^-20, V₈=V₆*,

V₉=V₁* V₁₀=V₄*,

V₁₁=V₃*, V₁₂=V₂*, V₁₃= A{116}B{116}2^-32

Это разбиение получено путем задания центрально-симметричного фрагмента Vi = - A{n-Li+l  п} B{n-Li+1 п} 2^-2n, где Li = 2(E(k/4)+1, разделяющем младшую часть матрицы на две подобные ей части, для каждой из которых повторяется процедура задания фрагмента до получения L_i<=1. Далее эта процедура повторяется для частей фрагментов, оказавшихся в старшей части матрицы.

Контрольные коды K_ai K_bi, образующих Ai Вi складываются из разрядов операндов или вычисляются в процессе их свертки по модулю..

Для рассмотренного примера разбиения матрицы и контроля по модулю т=3 составляемыми контрольными кодами КAi KBi являются КА₂=А{5}, КАз=А{5,6}, КА₄=А{7}, КА₆=А{9}, КА₇=А{9,10}, KA₈=A{11}, КА₁₀=А{13}, KA₁₁=A{13,14}, KA₁₂=A{15}, а также КВ₂=В{15}, КВз=В{13,14}, КВ₄=В{13}, KB₆=B{11}, КВ₇=В{9,10}, KB₈=B{9}, КВ₁₀=В{7}, КВ₁₁=А{5,6}, КВ₁₂=В{5}.

Контрольные коды КА₁₃, KB₁₃ являются входными контрольными кодами операндов: KA₁₃=KA, KB₁₃=KB.

Другие контрольные коды вычисляются:

KA₁=(KA₃+A{7,8})mod3,

КА₉=(КА₁₁+А{15,16})mod3,

КА₅=(КА₇+А{11,12}+KA₉)mod3,

KA{116}==(A{14}+KA₁+KA₅)mod3,

KB₁=(KB₃+B{15,16})mod3,

КB₉=(КB₁₁+B{7,8})mod3,

КB₅=(КB₇+B{11,12}+KB₁)mod3,

KB{116}==(B{14}+KB₉+KB₅)mod3,

В рассмотренном разбиении размеры одних фрагментов отличаются от размеров других с удвоенным шагом. Это

способствует наибольшему распараллеливанию контрольных вычислений и наименьшим затратам времени на контроль.

Сравнивая между собой достоинства и недостатки контроля по тем или другим модулям вида т=2^l-1, отметим:

1. Наиболее экономичным является контроль по модулю т=3. Этому способствует наименьшая длина l=2, а кроме того, принадлежность его также к модулям вида m1=2^l1+1, свойства которых позволяют дополнительно упрощать свертку чисел и операции над контрольными кодами. По мере возрастания величины l контроль по модулю т усложняется.

2. Вероятность обнаружения произвольных ошибок Р₀ возрастает при выборе для контроля большего по величине модуля т. Например, выбор т = 3 обеспечивает Р₀= 2/3, а т = 15 определяет P₀ = 14/15.

Кроме рассмотренных модулей т важное место в контроле занимает также цифровой модуль два, обеспечивающий контроль по четности или нечетности. Контрольный код числа по цифровому модулю два состоит из одного разряда, равного единице, если количество единиц в числе нечетное, и нулю - в противном случае. Проверка операции сложения основывается на контрольном соотношении

kakbkpks,

где КА, KB, KS - контрольные коды по цифровому модулю два слагаемых А, В и суммы S=A+B;

КР - контрольный код числа Р, составленного из межразрядных переносов, образуемых при сложении чисел А и В.

Цифровой модуль два широко используется для проверки хранения и передачи информации. Для этого вместе с числом хранится или передается его контрольный код, который в дальнейшем сравнивается с числом.

№ 33. Точность представления чисел и выполнения арифметических операций.

4.1. Точность вычислений

Запись числа в машинных кодах выполняется в пределах разрядной сетки. Это ограничивает точность представления чисел поскольку может привести к несовпадению истинного значения величины и ее значения в машинном формате. Разность между истинным значением величины А и ее машинным представлением называется абсолютной погрешностью представления А = А - Ам. Отнесение абсолютной погрешности А к величине Ам характеризует относительную погрешность представления А= А /Ам. Непосредственное отбрасывание младших разрядов, непомещающихся в разрядной сетке, приводит к абсолютной погрешности А <= а, где а - вес младшего разряда числа с фиксированной точкой, или вес младшего разряда мантиссы числа с плавающей точкой (с учетом порядка). Отбрасывание двоичных разрядов с округлением числа А до ближайшего значения Ам определяет величину ДА < а/2.

Относительная погрешность представления чисел с фиксированной точкой существенно зависит от величины Ам и для минимального значения Ам=а достигает в случаях непосредственного отбрасывания разрядов и отбрасывания с округлением соответственно значений 1 и 1/2. Относительная погрешность чисел с плавающей точкой для нормализованных мантисс в указанных случаях не превышает соответственно значений 2^l-1 где n - разрядность мантиссы.

Точность представления чисел ограничивает точность результата арифметической операции. Определим абсолютные погрешности для результатов сложения, умножения и деления чисел.

Результат сложения чисел А = Ам + А и В = Вм + В определяется суммой машинных значений: Ам+Вм, что отличает его от истинного значения на величину абсолютной погрешности

(А+В)= А+В.

Результат умножения чисел А и В определяется произведением машинных значений Ам и Вм, что отличает его от истинного значения А*В = АмВм + АмВ + ВмА +А-В на величину абсолютной погрешности, равной (с учетом малости А и В)

(А В) = АмВ + Вм А.

Абсолютная погрешность деления А/В определяется по формуле:

Относительные погрешности арифметических операций определяются по формулам:

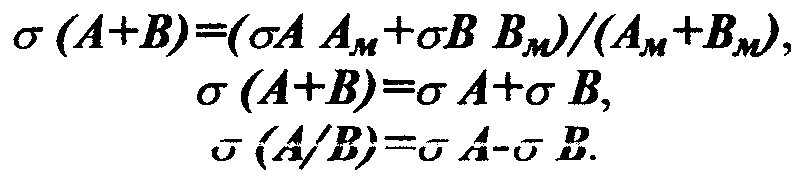
4.2. Достоверность выполнения арифметических операций в ЭВМ

Результат машинного выполнения операции может отличаться от истинного значения не только за счет погрешности представления чисел, но и вследствие возникновения неисправности в вычисляющем устройстве, что приводит к ошибке в результате.

Неисправности устройств являются, как правило, следствием дефектов их изготовления, прогрессирующих и проявляющихся в условиях эксплуатации этих устройств. Проявлению дефектов способствует отклонение режимов работы устройств от рекомендованных в установленных нормах (чрезмерные колебания напряжения источников питания, нарушение температурного режима, вибрация, радиация и т. д.). По характеру проявления дефектов неисправности вычислительных устройств делятся на сбои (кратковременные самоустраняющиеся неисправности) и отказы - устойчивые нарушения работоспособности устройства.

Подверженность устройств неисправностям создает проблему доверия к результатам машинного выполнения операций. С позиции этой проблемы устройства характеризуются достоверностью функционирования, определяемой знаниями о правильности работы этих устройств. Информация о правильной работе оценивается вероятностью Р безотказной работы устройства, которую можно рассчитывать, исходя из состава устройства и срока ' службы комплектующих его деталей. Соответственно величина 1-Р определяет вероятность, неправильной работы устройства и составляет резерв информации, за счет которой может быть увеличена достоверность. Данный резерв реализуется путем диагностирования устройства, т. е. контроля правильности его функционирования.

С учетом контроля достоверность определяется по формуле:

D=P+(l-P)Po,

где р₀ - вероятность обнаружения ошибок контролем, а (1-Р) Р₀ -величина, определяющая знания о неправильной работе устройства.

По способу реализации контроль классифицируется как программный, аппаратный или комбинированный, т. е. программно-аппаратный. К программному контролю относится, например, двойной счет (повторное решение задачи). Примером аппаратного контроля является дублирование устройства, т.е. решение задачи на двух устройствах с последующей сверкой вычисляемых результатов. Комбинированный контроль имеет место при аппаратной поддержке программного контроля, например в случае двойного счета произведения с аппаратно реализуемой сменой мест сомножителей.

Различают функциональное и тестовое диагностирование. Тестовое диагностирование выполняется в паузах основной работы устройства на контрольных примерах, обеспечиваемых специально подаваемыми входными воздействиями - тестами - в порядке профилактики неисправностей устройства или для локализации места неисправности. При этом результаты решения контрольных задач сравниваются с рассчитанными ранее или с результатами работы эталонного устройства и делается вывод о правильности функционирования проверяемого устройства.

Тестовое диагностирование определяет лишь потенциальную возможность правильного функционирования устройства и не дает гарантии получения правильного результата во время его основной работы. Тестовое диагностирование предполагает отвлечение устройства от решения основной задачи, что ограничивает производительность устройства и вовсе неприемлемо при непрерывной обработке информации. Этим объясняется важность функционального диагностирования, дающего оперативную оценку состояния проверяемого устройства.

Функциональное диагностирование выполняет проверку правильности вычислений в процессе работы устройства.

Организация контроля возможна только при наличии определенной информационной избыточности, создаваемой за счет ресурсов времени и аппаратуры, т. е. временной и структурной избыточностей в решении задач контроля. Программный и аппаратный контроль используют в качестве основной соответственно временную и структурную избыточность.

№34. Микропроцессоры 2 и 3-го поколения фирмы Intel.

Микропроцессор – это функционально законченное , программно - управляемое устройство, реализуемое в виде БИС или СБИС. Микропроцессор содержит как правило следующие функциональные устройства:

1. УУ(устройство управления)

2. АЛУ

3. Регистры общего назначения

4. Интерфейсные схемы для организации вешнего интерфейса МП

По системе команд микропроцессоры (МП) делят на 5 поколений:

1. 4-х разрядные ПМОП МП (в калькуляторах);

2. 8-ми разрядные НМОП МП;

3. 16-ти разрядные НМОП МП

4. 32-х разрядные КМОП МП

5. 64-х разрядные КМОП МП

Структура однокристального МП Intel 8080, аналог, выпускаемый у нас – КР580ИК80А.

Сложность данного МП – 5000 вентелей на кристалле;

Тактовая частота – 2 МГц;

Быстродействие – 500000 операций в секунду;

Число базовых команд – 78

Uпитания +12V, +5V и –5V.

Программная модель данного МП. Набор регистров, доступных для программиста

А
В	C
D	E
H	L
ПС
УС

К

К

аждая команда содержит от одного до 5 машинных циклов. Каждый цикл содержит от 3 до 5 машинных циклов.

Ц1

Ц2

Ц3

Ц4

Ц5

Т1

Т2

Т3

Т4

Т5

Адресация и система команд данного МП:

1. непосредственная адресация (операция указывается непосредственно в команде)

2. прямая, в этом случае адрес ячейки памяти указывается непосредственно в команде.

3. Регистровая – номер регистра указывается непосредственно в команде.

4. Косвенная – адрес ячейки памяти указывается через регистровую пару H+L МП