4.6.2. Циклические коды.

Циклическими называются коды, в которых часть или все кодовые комбинации могут быть получены путём циклического сдвига одной или нескольких исходных комбинаций этого кода. Сдвиг осуществляется справа налево с переносом левого символа в конец.

Операции над многочленами. Любой двоичный вектор может быть представлен в виде многочлена.

1011->1*X³+0*X²+1*X¹+1*X⁰

Существует 2 операции:

Умножение. (аналогично умножению многочленов)

Последовательное умножение на Х аналогично циклическому сдвигу влево на один разряд.

Деление.(аналогично делению многочленов)

Построение циклического кода.

Построение циклических кодов базируется на использовании неприводимых в поле двоичных чисел многочленов.

Неприводимыми называются многочлены, которые не могут быть представлены в виде произведения многочленов низших степеней. Аналогом неприводимых многочленов являются простые числа, которые делятся без остатка только на себя и на единицу.

Таблица неприводимых многочленов.

1	2	3	4
1	111	1011	10011
		1101	11111
			11100
			11001

Метод 1.

1. Определяем n, n_u, n_k.

2. Выбираем образующий многочлен из числа неприводимых, так чтобы его степень была больше либо равна n_k, а вес был больше либо равен d₀.

3. Строим образующую матрицу путём умножения строк единичной матрицы на образующий многочлен.

4. Все остальные кодовые комбинации получаем путём суммирования по модулю 2 всевозможных комбинаций строк образующей матрицы.

Например:

1. n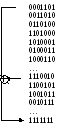_u=4 -> n_k =3,n=7.

2. Т.к. d0=3, то получаем многочлен X³+X²+1.

3. Строим образующую матрицу:

0001*1101=||0001101||

0010*1101=||0011010||

0100*1101=||0110100||

1000*1101=||1101000||

4. Находим остальные кодовые комбинации:

12-> 0010111

13->0111001

14->1100101

2З->0101110

24->1110010

З4->1011100 12З->0100011 124->1111111 …

Построив все кодовые комбинации, сгруппируем их следующим образом:

Осуществив группировку кодовых комбинаций, в явном виде можно увидеть свойство цикличности, присущее всем кодовым комбинациям.

Метод 2.

1. Определяем n, n_u, n_k.

2. Выбираем образующий многочлен из числа неприводимых так, чтобы его степень была больше либо равна n_k , а вес был больше либо равен do.

3. Строим кодовые комбинации путём умножения информационной части на образующий многочлен.

Например

1. n_u=4 -> n_k =3,n=7.

2. Т.к. d0=3, то получаем многочлен X³+X²+1.

3. 0001x1101=0001101; 0010x1101=0011010; 0011x1101=0010111. Итд.

Аналогично строим все последующие кодовые комбинации.

Обнаружение и коррекция ошибок.

1. Принятая кодовая комбинация делится на образующий многочлен.

2. Если остаток от деления равен нулю, то ошибок нет. Конец алгоритма.

3. Если вес остатка меньше либо равен кратности корректируемых ошибок S, то делимое складывается по модулю 2 с остатком, что является коррекцией ошибки.

4. Если вес остатка больше кратности корректируемых ошибок, то осуществляется циклический сдвиг влево и снова полученная кодовая комбинация делится на образующий многочлен.

5. Пункты 3 и 4 повторяются до тех пор пока вес остатка не станет меньшим либо равным кратности корректируемых ошибок.

6. Скорректированную кодовую комбинацию сдвигаем циклически вправо столько раз, сколько было сдвигов влево.

№107. Семантический разрыв между архитектурой ЭВМ и языками высокого уровня.