1.5. Граничные условия для векторов электромагнитного поля

Поверхности физических тел являются границами, разделяющими среды с разными свойствами. В рамках макроскопической электродинамики принято считать, что при переходе через эти поверхности параметры сред меняются скачком. Такие поверхности называютсяграницами раздела.

Согласно уравнениям Максвелла при этом неизбежно испытывают скачки некоторые векторы поля. Для решения задач электродинамики, помимо уравнений Максвелла, необходимо знать граничные условия – соотношения между векторами в двух очень близких точках, находящихся по обе стороны границы раздела двух сред. Граничные условия являются следствием уравнений Максвелла в интегральной форме.

Пусть достаточно гладкая поверхность разделяет две среды, в каждой из которых параметры либо постоянны, либо меняются медленно от точки к точке. Тогда в малой окрестности любой точки на поверхностиS можно считать границу плоской, а параметры сред – неизменными. Таким образом, из рассмотрения исключаются точки, лежащие вблизи изломов и резких изгибов границы или в области быстрого изменения параметров хотя бы одной из сред.

Рассмотрим некоторую поверхность S, разделяющую две среды с параметрами и(рис. 1.2).

В каждой точке поверхности S можно провести касательную плоскость P и три единичных вектора: – нормаль, направленная из второй среды в первую;– векторы, лежащие в плоскостиР (касательные к границе раздела). При этом будем считать, что .

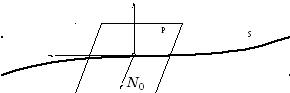
Рисунок 1.2 – Две среды, разделенные поверхностью S

Используя уравнения Максвелла в интегральной форме, можно показать (см. Приложение В), что на поверхности S выполняются следующие равенства:

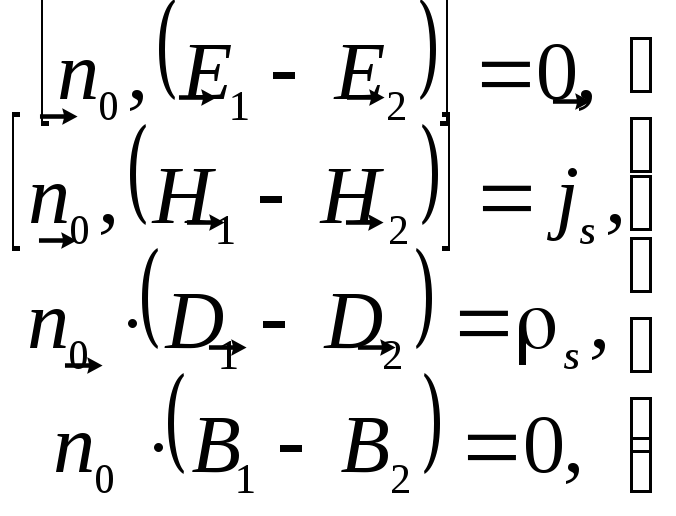(1.21)

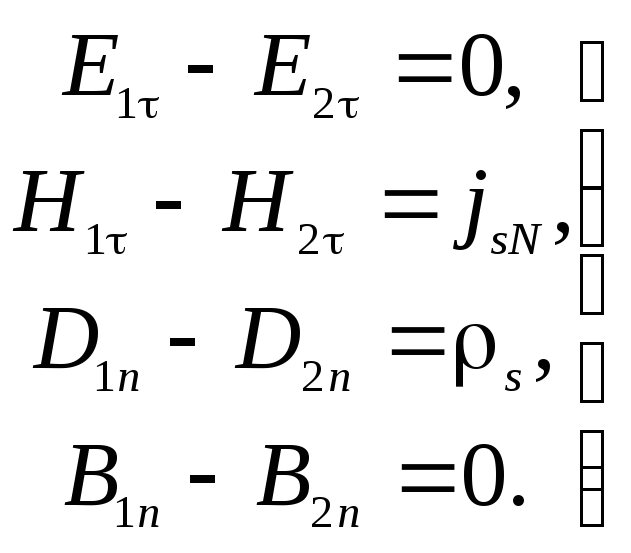. (1.22)

Соотношения (1.21) называют граничными условиями в векторной, а соотношения (1.22) – в скалярной форме. Из этих соотношений следует, что касательные составляющие Е_1τ и Е_2τ вектора и нормальные составляющиеВ_1n и В_2n вектора при переходе через границу раздела сред всегда непрерывны. Касательные составляющие Н_1τ и Н_2τ вектора и нормальные составляющиеD_1n и D_2n вектора непрерывны только в том случае, если на границе раздела сред отсутствуют соответственно ток с поверхностной плотностьюи заряды с поверхностной плотностью.

Пусть одна из сред, например, вторая является идеальным проводником. Из уравнений Максвелла следует, что в идеальном проводнике ( = ) электромагнитное поле отсутствует. Учитывая этот факт и соотношения (1.21) получаем, что на поверхности идеального проводника граничные условия имеют следующий вид:

, .

Из последних соотношений следует, что силовые линии вектора всегда перпендикулярны, а силовые линии векторавсегда касательные к поверхности идеального проводника.

Используя граничные условия (1.21), (1.22) и материальные уравнения (1.9), (1.10), можно записать граничные условия для касательных составляющих векторов ии нормальных составляющих векторови.