Раздел 5 распространение электромагнитных волн

5.1. Законы Снеллиуса. Коэффициенты Френеля

При рассмотрении вопросов распространения электромагнитных волн в случае наличия Земли и атмосферы необходимо учитывать явления, которые происходят при падении плоских волн на границу раздела двух сред; при дифракции волн; при распространении волн в неоднородной среде и пр.

Рассмотрим вначале явления происходящие при падении плоских волн на плоскую границу раздела двух сред. Пусть границей раздела является плос­костьYOZ, которая разделяет две среды с различными параметрами (рис. 5.1). Пусть на границу раздела падает плоская волна под углом . Выясним, какие волновые процессы происходят на границе раздела (плоскость YOZ).

Эту задачу удобно (и наиболее просто) рассматривать отдельно для двух случаев поляризации, когда у падающей волны вектор перпенди­кулярен плоскости падения (нормально поляризованная волна) и когда у падающей волны вектор перпендикулярен плоскости падения (параллельно поляризованная волна). Плоскостью падения называется плоскость, проходящая через нормаль к границе раздела и направление распространения волны (в рассматриваемом случае плоскость XOZ является плоскостью падения).

Представим электромагнитное поле в первой среде в виде суммы падающей и отраженной плоской волны, а во второй – в виде преломленной плоской волны.

В случае нормальной поляризации комплексные амплитуды вектора падающей, отражённой и преломлённой волн представим в следующем виде:

, (5.1)

, (5.2)

, (5.3)

где ,и– углы падения, отражения и преломления;и– коэффициенты отражения и преломления нормально поляризованной волны;и– комплексные (в общем случае) волновые числа первой и второй среды соответственно.

Из формул (5.1) – (5.3) видно, что коэффициенты иможно определить следующим образом.Коэффициентом отражения (преломления) для нормально поляризованной волны называется величина, равная отношению комплексной амплитуды вектора отраженной (преломленной) и комплексной амплитуды вектора падающей волны на границе раздела.

Отметим, что комплексные амплитуды векторов , соответствующие комплексным амплитудам, определяемым соотношениями (5.1) … (5.3), легко найти, используя второе уравнение Максвелла для комплексных амплитуд, которое имеет следующий вид (см. соотношения (1.36)):

. (5.4)

В случае параллельной поляризации комплексные амплитуды вектора падающей, отражённой и преломлённой волн представим в следующем виде:

, (5.5)

, (5.6)

. (5.7)

где и– коэффициенты отражения и преломления параллельно поляризо­ванной волны.

Из формул (5.5) … (5.7) видно, что коэффициенты иможно определить следующим образом.Коэффициентом отражения (преломления) для параллельно поляризованной волны называется величина, равная отношению комплексной амплитуды вектора отраженной (преломленной) и комплексной амплитуды вектора падающей волны на границе раздела.

Отметим, что комплексные амплитуды векторов , соответствующие комплексным амплитудам, определяемым соотношениями (5.5) … (5.7), легко найти, используя первое уравнение Максвелла для комплексных амплитуд, которое имеет следующий вид (см. соотношения (1.36)):

. (5.8)

Величины ,,и, входящие в соотношения (5.1) … (5.3) и (5.5) … (5.7) называютсякоэффициентами Френеля.

Используя граничные условия (1.22) и формулы (5.1) … (5.8) нетрудно получить следующие выражения для определения неизвестных нам величин, входящих в формулы (5.1) … (5.7) (углы отражения и преломления и коэффициенты Френеля). Эти выражения имеют следующий вид:

₁ = , (5.9)

, (5.10)

, (5.11)

, (5.12)

, (5.13)

, (5.14)

где и– комплексные (в общем случае) волновые сопротивления первой и второй среды соответственно,

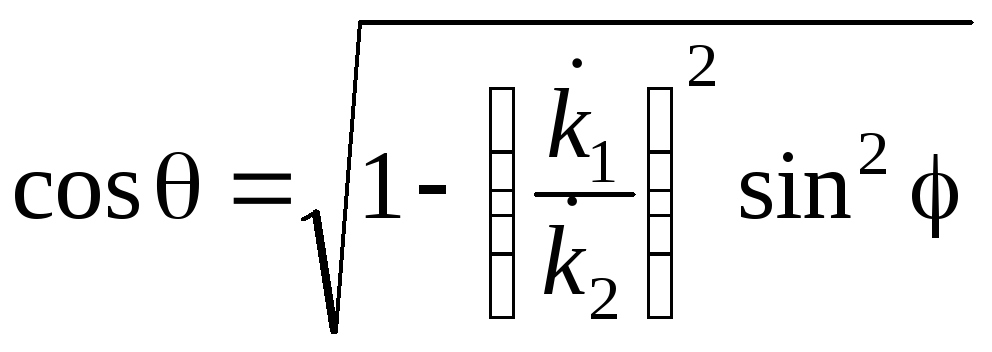. (5.15)

Равенства (5.9) и (5.10) при действительных и(обе среды без потерь) называют первым и вторым законами Снеллиуса.

Из формул (5.11) … (5.14) видно, что коэффициенты Френеля в общем случае являются комплексными величинами и зависят как от параметров обеих сред, так и длины волны (если хотя бы одна из сред имеет потери). В следующих разделах будет проведен анализ коэффициентов Френеля для некоторых практически важных случаев.

Пусть на границу раздела падает волна круговой или эллиптической по­ляризации. В этом случае падающую волну целесообразно представить в виде суперпозиции двух волн, одна из которых поляризована нормально, другая – параллельно. Определяя для каждой из этих волн коэффициенты отражения и преломления (по формулам (5.11) … (5.14)) легко определить параметры отраженной и преломленной волн.

Рассмотрим случай, когда вторая среда является анизотропной средой, и когда вол­новые числа второй среды различны для нор­мально и параллельно поляризованных волн. Пусть на границу раздела падает вол­на, представимая в виде суммы нормально и параллельно поляризованных волн. Выясним, что будет происходить с этой волной на гра­нице раздела. Из законов Снеллиуса следует, что в первой среде появиться отраженная вол­на, а во второй среде возникнуть две волны, идущие в различных направлениях (рис 5.2). Этот факт называется явлением двойного лучепреломления. В теории распространения волн в ионосфере одну из этих волн называю обыкновенной волной, другую необыкновенной.

Отметим, что коэффициенты Френеля, определяемые формулами (5.11) … (5.14), в большинстве практически важных случаев можно использовать при расчетах коэффициентов отражения (преломления) от поверхности Земли.