3.4. Плоскость в пространстве

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Керченский государственный морской технологический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Lektsii_vyssh_matem.pdf

Скачиваний:

Добавлен:

08.02.2016

Размер:

1.46 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 159 10 11 12 13 14 15 > Следующая >>>

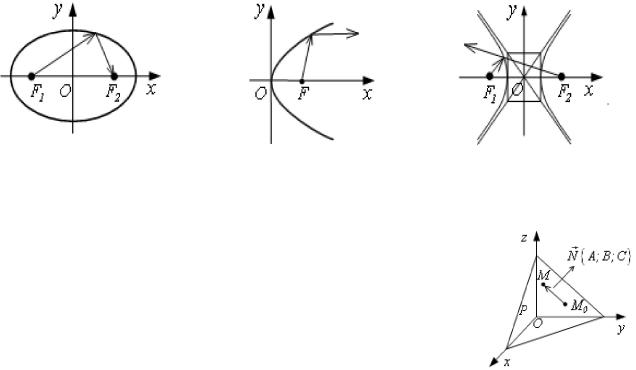
Все кривые 2-го порядка являются коническими сечениями (рис.3.14). Оптические свойства кривых 2-го порядка.

1)Если источник света находится в одном из фокусов эллиптического зеркала , то лучи его, отразившись от зеркала, собираются в другом фокусе.

2)Если источник света находится в фокусе параболического зеркала, то лучи его, отразившись от зеркала, идут параллельно оси параболы.

3)Если источник света находится в одном из фокусов гиперболического зеркала, то лучи его, отразившись от зеркала, идут далее так, как если бы они исходили из другого фокуса (рис. 3.15).

		Рис. 3.15
3.4.	Плоскость в пространстве
3.4.1. Общее уравнение плоскости
M0 M x x0 ; y y0 ; z z0 P ;
вектор N A,B,C		– вектор нормали Р; N M0 M и
N M0 M 0 , т. е.		A x x0 B y y0 C z z0 0 . Этот тип
уравнения называется связка плоскостей с центром в т.М0.
Раскроем скобки в уравнении и обозначим чис-
ло D Ax0	By0 Cz0 , получим общее уравнение плоскости:		Рис. 3.16

Ax By Cz D 0 , где числа А, В, С есть координаты вектора нормали N плоскости Р.

Примеры . 1) Найти уравнение плоскости, проходящей через т.М0(1; 1; -1)

иперпендикулярно вектору OM 0 .

2)Построить плоскость 2x+3y+z-6=0 и найти углы нормали плоскости с осями координат.

3.4.2. Неполные уравнения плоскости

1)D 0 , плоскость проходит через начало координат.

2)A 0 , плоскость параллельна ОХ;

А= 0; D 0 , плоскость проходит через ОХ.

3)В = 0, плоскость параллельна ОY;

В = 0,	D 0 , плоскость проходит через ОY.
4) C = 0, плоскость параллельна ОZ;
С = 0,	D 0 , плоскость проходит через ОZ.

5)А = 0; В = 0, плоскость параллельна координатной плоскости XOY.

6)А = 0; C = 0, плоскость параллельна координатной плоскости XOZ.

7)В = 0, C = 0, плоскость параллельна координатной плоскости YOZ.

8)x = 0 – уравнение координатной плоскости YOZ;

у = 0 – уравнение плоскости ХOZ; z = 0 – уравнение плоскости XOY.

3.4.3. Уравнение плоскости в отрезках

Р: Ах + Ву + Сz + D = 0;

Ax By Cz D

: D ; тогда

D A

D B

D C

Обозначим числа D

a ; D

b ;

c ,

получим уравнение плоскости

в отрезках:

1, где –

a, b, c отрезки, отсекаемые плоскостью на осях

координат

Примеры.

1) Найти уравнение плоскости Р: 2x 3y 6 z 12 0 в отрез-

ках и построить Р. Найти углы N с осями координат.

2) Построить плоскости: 2х + 3у – 6 = 0;

3х – 6 = 0; 2у + 6 = 0; 3х = 0 и

указать их нормали.

3.4.4. Уравнение плоскости, проходящей через три заданные точки

M1M x x1 ; y y1 ;z z1 ;

M1M 2 x2 x1 ; y2 y1 ;z2 z1 ;

Рис. 3.17

M1M 3 x3

x1 ; y3 y1 ;z3

z1 .

Эти векторы расположены в одной плоскости, следовательно, компланарны,

и их смешанное произведение равно нулю.	x x1	y y1	z z1
М1M М1M2 М1M2 0 или	x x1	y y1	z z1
М1M М1M2 М1M2 0 или	x2 x1	y2 y1	z2 z1	0 .
	x3 x1	y3 y1	z3 z1

Это уравнение является уравнением плоскости через три заданные точки.

Пример. Найти уравнение плоскости, проходящей через точки М1(1;2;3); М2(0;1;1); М3(-1;-;0). Указать N и найти ее длину.

3.4.5. Взаимное расположение двух плоскостей в пространстве

P1 : A1x B1 y C1z D1 0 ,

N1 A1 ;B1 ;C1

P2 : A2 x B2 y C2 z D2 0 ,

N2 A2 ;B2 ;C2 .

P , тогда N

и, следовательно,

P1 P2 , тогда N1

N2 и, следовательно, A1 A2 B1B2

C1C2 0 .

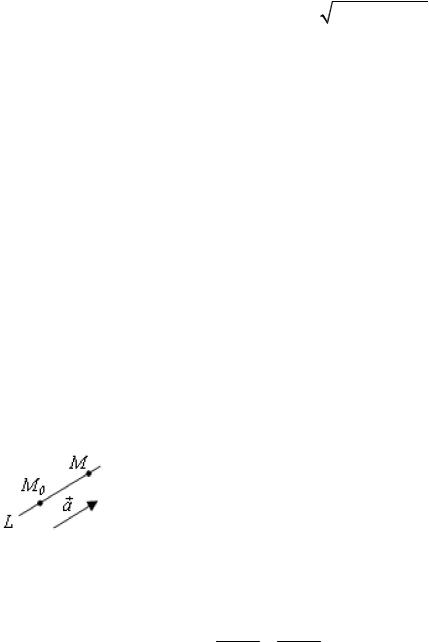
3) Углом φ между Р1 и Р2 называется любой из двух

двугранных углов, образованных этими плоскостями.

cos

Рис. 3.18

Примеры.

1) Найти угол φ между Р1 :2x 3y z 5 0 и Р2 : x y z 0 .

2)	Проверить P1	P2 ?	Р1 : x y 2z 4 0 ;	Р2 : 2x 2y 3z 4 0 .
3)	Проверить P1	P2 ?	Р1 : 2x y z 3 0 ;	Р2 : x 2y 4 0 .

3.4.6. Расстояние от точки до плоскости

Пусть уравнение плоскости имеет вид P: Ax +By+Cz+D = 0, точка M0 имеет координаты (x0 , y0 , z0). Тогда расстояние от точки до плоскости вычисляется по формуле:

d(т.M0; P)	Ax0 By0 Cz0 D		.



		A2 B2 C2
Примеры . 1) Найти длину перпендикуляра, опущенного из т. А0(1;2;1) на
плоскость Р : x y 2z 0 .
2) Найти расстояние от плоскости	2x 3y z 4 0 до начала координат.

3.4.7. Геометрический смысл СЛАУ

Если СЛАУ (n = 3) имеет единственное решение, то три плоскости имеют одну точку пересечения.

Если СЛАУ имеет бесконечно много решений, то три плоскости имеют общую линию пересечения.

Если СЛАУ несовместна, то три плоскости не имеют никаких общих пересечений (ни точки, ни линии).

3.5. Прямая линия в пространстве 3.5.1. Общие уравнения прямой

Прямую L в пространстве можно определить как результат пересечения

двух плоскостей: A1x B1 y C1z D1 0 A2 x B2 y C2 z D2 0.

3.5.2. Канонические уравнения прямой

ax ,ay

,az L, т.е. является ее направля-

Пусть т. M0 x0 , y0 ,z0 L и вектор a

ющим вектором; т. M x,y,z L и является текущей.

Тогда вектор M0M x x0 ; y y0 ;z z0 коллинеарен вектору a ,

следовательно,

x x0

y y0

z z0

. Эти уравнения называ-

Рис.3.19

ются каноническими уравнениями прямой в пространстве.

Точка M0 x0 ,y0 ,z0

называется опорной точкой прямой.

x x0

y y0

Приведение к общему виду:

x x

z z

ax az .

3.5.3.Параметрические уравнения прямой0 0

x x0

x x a

x x

y y

z z

t ,

t – параметр. Тогда y y0

или

y y

z z

z z0

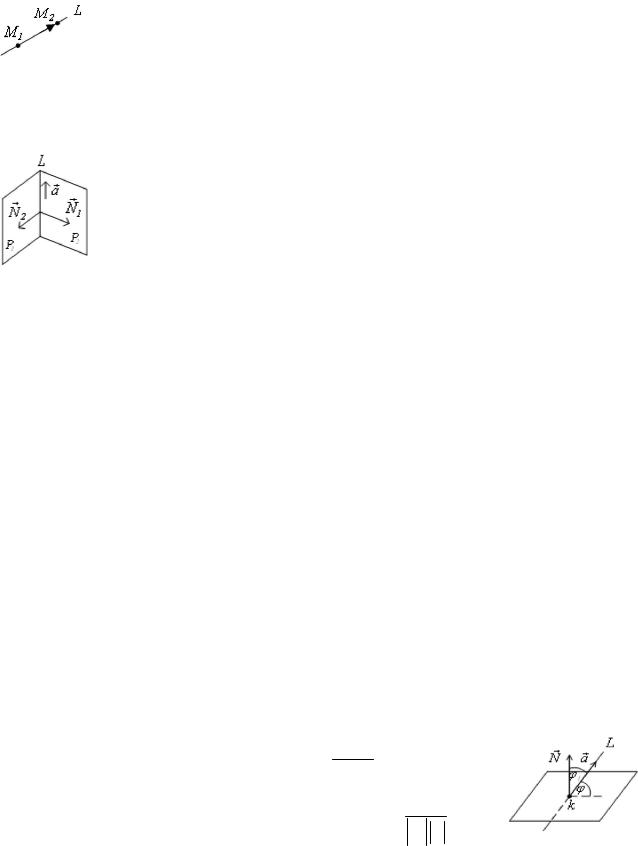
Эти уравнения называются параметрическими уравнениями прямой.

Физический смысл: M0 x0 ,y0 ,z0

– точка начала прямолинейного движе-

ax ,ay ,az ;

т. M x,y,z

– положение ма-

ния материальной точки со скоростью a

териальной точки в пространстве в момент времени t.

3.5.4. Прямая, проходящая через две заданные точки

Пусть т. M1 x1 ,y1 ,z1 –

опорная точка прямой,

т.

M2 x2 ,y2 ,z2

расположена на прямой, вектор

M1M2 x2

x1 ; y2

y1 ;z2 z1 –

Рис. 3.20

направляющий вектор прямой.

Тогда уравнения прямой имеют вид

x x1

y y1

z z1

x x

3.5.5. Приведение общих уравнений прямой к каноническому виду

L : A1x B1 y C1z D1 0 ; A2 x B2 y C2 z D2 0

N1 A1 ;B1 ;C1 ;

N2 A2 ;B2 ;C2 .

;az

;

N2 .

a ax ;ay

a N1

a N2

, следовательно, a N1

Рис. 3.21

В качестве опорной точки возьмем точку пересечения этой пря-

мой с какой-нибудь координатной плоскостью, например, XOY:

A1 x B1 y C1 z D1 0

;

A1 x B1 y D1 0

A x B

y C

z D

A x B

y D

0 , в результате решения

z 0

СЛАУ получим т. М0(х0, у0, 0).

3.5.6. Взаимное расположение прямой и плоскости

или ax A ay B az C 0 .

P , тогда a N1

a N 0

, тогда a

3) Чтобы найти точку пересечения L и P, надо уравнение прямой взять в параметрическом виде, уравнение плоскости - в общем виде. Получим систему:

x x0 axt

y y0 ayt

z z0 azt

Ax By Cz D 0.

Неизвестным является параметр t. Имеем фактически одно уравнение с одним неизвестным A x0 axt B y0 ayt C z0 azt D 0 . Решив уравнение, получим значение параметра t для точки пересечения L и P. Далее найдем координаты x, y, z этой точки.

4) Угол φ между прямой L и плоскостью Р.

; 1

;

cos 1

;

	2
				N a
cos 1 cos		sin .	Следовательно, sin	N	a
						.

Рис. 3.22

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 159 10 11 12 13 14 15 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
20.04.2019429.06 Кб3l (1).doc
#
08.02.2016419.33 Кб7Lab1.doc
#
08.02.2016515.33 Кб5Lab_2_Спецификации+физической+среды+Ethernet.pdf
#
08.02.201691.14 Кб17Lekcii_ravnovesie_po_Nehshu.doc
#
08.02.20163.5 Mб300lektsii_SM-2utverzhd.doc
#
08.02.20161.46 Mб29Lektsii_vyssh_matem.pdf
#
08.02.201659.86 Кб54Metodicheskie_ukazania_kr.docx
#
08.02.20161.6 Mб574Metodichka_po_voprosam_dlya_Sevastopolya.docx
#
08.02.2016688.13 Кб381Met_ukaz_Prakt_Makro_2009_ispr_2015.doc
#
19.08.2019100.86 Кб5Modul_OOT_dlya_MA.doc
#
08.02.2016107.09 Кб17moy_kursach нинидзе тсс.docx

Плоскость в пространстве

3.4.1. Общее уравнение плоскости

3.4.2. Неполные уравнения плоскости

3.4.5. Взаимное расположение двух плоскостей в пространстве

3.5.2. Канонические уравнения прямой

3.5.3.Параметрические уравнения прямой0 0

3.5.6. Взаимное расположение прямой и плоскости