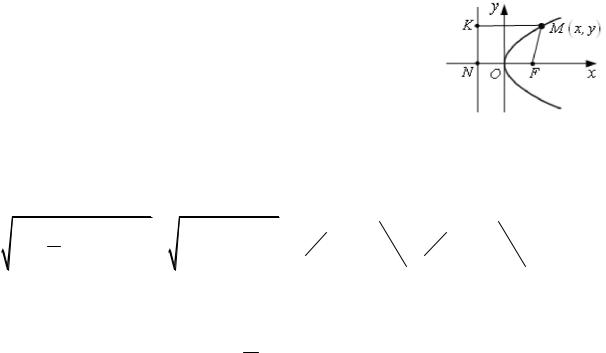
б) Уравнение смещенной гиперболы.
Если центр гиперболы расположен в т. С(α;β), то ее уравнение примет вид
|
|
|
|
|
|
x 2 |
|
|
y |
1. |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
a2 |
|
|
|
b2 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x x' |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
получим уравнение |
||||||||
Сделаем параллельный перенос координат в т.C : |
|
|
|
, |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y y' |
|
|
||||||
гиперболы в каноническом виде |
|
x'2 |
|
|
y'2 |
1. Строим гиперболу по канониче- |
|||||||||||||||||||||||
|
a2 |
|
|
|
b2 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
скому уравнению в новой системе координат X ' CY ' . |
|
|
|
|
|||||||||||||||||||||||||
|
Аналогично поступаем, если сопряженная гипербола задана в смещенном |
||||||||||||||||||||||||||||
виде: |
|
|
x 2 y 2 |
|
|
|
|
|
|
|
|
x 2 y 2 1 . |
|||||||||||||||||
|
|
|
|
1 |
|
|
или |
||||||||||||||||||||||
|
|
|
|
a 2 |
b 2 |
|
|
|
|
|
|
|
|
|
|
|
a 2 |
|
|
|
|
b 2 |
|
|
|||||
|
Сделав параллельный перенос, получим каноническое уравнение вида: |
||||||||||||||||||||||||||||
|
|
|
|
|
x'2 |
|
y'2 |
1 |
|
|
|
или |
|
|
x'2 |
|
y'2 |
|
1. |
|
|
||||||||
|
|
|
|
a2 |
b2 |
|
|
|
|
a2 |
b2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Пример. Назвать и построить линию |
|
|
x 1 2 |
|
|
|
|
y 2 2 |
|
1 . |
||||||||||||||||||
|
|
|
|
|
9 |
|
|||||||||||||||||||||||
|
3.3.4. |
Парабола – ГМТ плоскости, |
|
|
4 |
|
|
|
|
|
|
||||||||||||||||||
|
равноудаленных от фиксированной |
||||||||||||||||||||||||||||
точки плоскости – фокуса F – и от прямой, называемой директрисой. |
|||||||||||||||||||||||||||||
|
а) Каноническое уравнение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Выбор системы координат: ось ОХ – прямая, прохо- |
|
|
|||||||||||||||||||||||||||
дящая через т.F перпендикулярно директрисе и пересека- |
|
|
|||||||||||||||||||||||||||
ющая директрису в т.N; NF = р. Ось ОY – срединный пер- |
|
|
|||||||||||||||||||||||||||
пендикуляр к отрезку NF. |
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
В данной системе координат т. F |
|
|
|
|
;0 |
|
, т. N |
|
|
|
;0 , |
|
Рис. 3.13 |
||||||||||||||||
2 |
2 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т. K |
|
|
; y |
, т.M x,y - текущая точка линии (3.13). |
|
|
|
|
|||||||||||||||||||||
2 |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Геометрическое свойство параболы: КМ = FМ.
p 2
x 2
y y |
2 |
|
|
p 2 |
2 |
|
|
2 |
|
p2 |
|
2 |
|
p2 |
|
2 |
|
||
|
|
x |
|
|
y |
|
; |
x |
|
xp |
|
x |
|
xp |
|
y |
|
; |
|
|
2 |
|
|
4 |
|
4 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
y2 2 px – каноническое уравнение параболы. Вершина параболы располо-
жена в т.О(0,0), ветвь направлена вправо, если p 0 , и направлена влево, если
p 0 . Уравнение директрисы: x 2p . Осью параболы является ось ОХ.
Если ось ОY проходит через фокус F параболы перпендикулярно директрисе, ось OX – срединный перпендикуляр к отрезку NF = р, то, проделав преобразования, получим каноническое уравнение параболы в виде х2 = 2ру. Вершина параболы расположена в т.О(0,0), ветвь направлена вверх при p 0 и направлена вниз
31
при p 0 ; фокус - |
|
|
p |
|
|
p |
|
||
F |
0; |
|
|
; директриса имеет уравнение |
y |
|
. Осью параболы |
||
2 |
2 |
||||||||
|
|
|
|
|
|
|
|||
является ось OY.
Парабола симметрична относительно своей оси.
Для построения параболы необходимо знать вершину и ось параболы, направление ветви и несколько дополнительных точек.
б) Уравнение смещенной параболы.
Если вершина параболы расположена в т.В(α; β), то уравнение смещенной параболы имеет вид
|
y 2 2 p x или |
x 2 2 p y . |
|
||
Сделаем параллельный перенос системы координат в т.В(α; β) по формулам |
|||||
|
|
x' x |
|
|
|
|
|
y' y |
, |
|
|
получим уравнение параболы в каноническом виде: y'2 |
2 px' или |
x'2 2 py' . |
|||
Строим параболу в новой системе координат X'ВY'. |
|
||||
Пример. Назвать и построить линии: |
|
|
1 x 2 . |
||
1) y2 4x ; |
2) x2 y ; |
3) x 2 2 4 y 1 ; |
4) y 1 2 |
||
|
|
|
|
|
4 |
3.3.5Общее уравнение кривой второго порядка
Уравнением кривой второго порядка в общем виде является выражение
Ax2 Bxy Cy2 Dx Ey F 0 , левая часть которого есть многочлен второго по-
рядка относительно х, у. При этом Ax2 Bxy Сy2 – квадратичная форма, Dx Ey
– линейная форма, F – свободный член.
Рассмотрим более простой случай уравнения при В=0:
Ax2 Cy2 Dx Ey F 0.
Выделив полный квадрат по х и у, получим одно из уравнений смещенной кривой. Далее, сделав параллельный перенос системы координат и соответствующую замену переменных, получим каноническое уравнение. По каноническому уравнению кривой в новых переменных х', у' строим кривую.
Пример. Назвать и построить линии:
1) x2 y2 2x 0 ; 2) 2 y x2 4x ; 3) 4x2 16 x 9 y2 54 y 101 0 .
Замечания.
1) Кривая 2-го порядка может вырождаться в пару прямых:
4x2 y2 0 ; 2x y 2x y 0 ; y 2x , y 2x.
2)Уравнение 2-го порядка может определять одну точку:
x2 y2 0 , точка О(0,0) или окружность нулевого радиуса.
3)Уравнение 2-го порядка может не определять никакого
геометрического образа: |
x2 |
|
y2 |
1 (мнимый эллипс). |
9 |
|
|||
|
4 |
Рис. 3.14 |
||
32